
题目列表(包括答案和解析)
6、已知一个直角三角形的两条直角边的长恰好是方程 的两个根,则这个直角三角形的斜边长是( )
的两个根,则这个直角三角形的斜边长是( )
A、 B、3
C、6
D、9
B、3
C、6
D、9
5、市政府为了申办2010年冬奥会决定改善城市容貌,绿化环境,计划经过两年时间,绿地面积增加44%,这两年平均绿地面积的增长率是( )
A、19% B、20% C、21% D、22%
4、已知关于 的方程
的方程 有实数根,则
有实数根,则 的取值范围是( )
的取值范围是( )
A、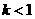 B、
B、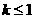 C、
C、 D、
D、
3、如果关于 的方程
的方程 的两个实数根互为倒数,那么
的两个实数根互为倒数,那么 的值为( )
的值为( )
A、 B、
B、 C、
C、 D、
D、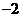
2、关于 的方程
的方程 的根的情况是( )
的根的情况是( )
A、有两个不相等的实数根 B、有两个相等的实数根
C、无实数根 D、不能确定
1、关于 的一元二次方程
的一元二次方程 的一个根是0,则
的一个根是0,则 的值为( )
的值为( )
A、 B、
B、 C、
C、 或
或 D、
D、
11.甲乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置, 我们用数轴Ox表示这条公路,原点O为零千米路标(如图),并作如下约定:

①速度v>0,表示汽车向数轴正方向行驶;速度c<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止.
②汽车位置在数轴上的坐标s>0,表示汽车位于零千米路标的右侧;汽车位置在数轴上的坐标s<0,表示汽车位于零千米路的左侧;汽车位置在数轴上的坐标s=0,表示汽车恰好位于零千米路标处.
遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数图像的形式画在了同一直角坐标系中,如图.
请解答下列问题:
(1) 就这两个一次函数图像所反映的两汽车在这条公路上行驶的状况填写如下的表格.
|
|
行驶方向 |
速度的大小(km)h |
出发前的位置 |
|
甲车 |
|
|
|
|
乙车 |
|
|
|
 (2)甲乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置;如不能相遇,请说明理由.
(2)甲乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置;如不能相遇,请说明理由.
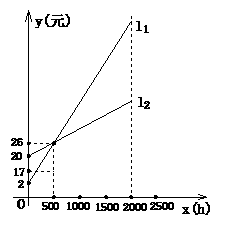
10.如图,L1、L2 分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数图像,假设两种灯的使用寿命都是2 000h,照明效果一样.
(1)根据图像分别求出L1、L2的函数关系式;
 (2)当照明时间为多少时,两种灯的费用相等?
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2 500h,他买了一个白炽灯和一个节能灯, 请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).
9.已知一次函数y=x+m的图像分别交x轴、y轴于A、B两点,且与反比例函数y= 的图像在第一象限交于点C(4,n),CD⊥x轴于D.
(1)求m、n的值,并作出两个函数图像;
(2)如果点P、Q分别从A、C两点同时出发,以相同的速度分别沿线段AD、CA向D、A运动,设AP=k.问k为何值时,以A、P、Q为顶点的三角形与△AOB相似?
8.在直角坐标系中,有以A(-1,-1),B(1,-1),C(1,1),D(-1,1)为顶点的正方形.设正方形在直线y=x上方及直线y=-x+2a上方部分的面积为S.
(1)求a=时,S的值.
(2)当a在实数范围内变化时,求S关于a的函数关系式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com