
题目列表(包括答案和解析)
例3 已知抛物线 交x轴于两点
交x轴于两点 .
.
又点P(4,n)在该抛物线上,设抛物线的顶点是C,求 的面积S。
的面积S。
分析:将 分成两个
分成两个 ,需求底边AD的长及相应的高,即点C、点P的纵坐标。为此,首先需确定抛物线的解析式。
,需求底边AD的长及相应的高,即点C、点P的纵坐标。为此,首先需确定抛物线的解析式。

解: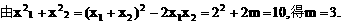
所以抛物线是
又由顶点C(1,4),P(4,-5)可得直线PC:y=-3x+7.再令y=0,得PC与x轴交点为
D( ,0).
,0).

例4 设直线l:y=2x+2交x轴于点A、交y轴于点B,一条抛物线过点A、点B及点(2,2),且与x轴的另一交点为D,顶点为C。求四边形ABCD的面积。
简解:将四边形分成三个三角形: 易由直线l:y=2x+2,得A(-1,0),B(0,2).
易由直线l:y=2x+2,得A(-1,0),B(0,2).
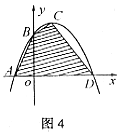
又过A、B及(2,2)的抛物线为 则顶点为
则顶点为 与x轴的另一交点为D(3,0)。
与x轴的另一交点为D(3,0)。
所以

解:画出示意图,直接求 的底边AB长和相应的高,比较困难。现割补法进行转化,记直线交x轴于点C,交y轴于点D,则所求面积
的底边AB长和相应的高,比较困难。现割补法进行转化,记直线交x轴于点C,交y轴于点D,则所求面积 
在y=-x+5中,分别令y=0,x=0,得C(5,0),D(0,5)。又由 
得A(4,1),B(1,4)
从而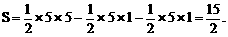
解:画出略图.可见 只要求出底边长和高(点C、A的横坐标).
只要求出底边长和高(点C、A的横坐标).

在
得C(3,2)

5. (08泰安)如图所示,
(08泰安)如图所示, 是直角三角形,
是直角三角形, ,以
,以 为直径的⊙O 交
为直径的⊙O 交 于点
于点 ,点
,点 是
是 边的中点,连结
边的中点,连结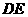 .
.
(1)求证: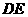 与⊙O相切;
与⊙O相切;
(2)若⊙O的半径为 ,
, ,求
,求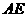 .
.
﹡6. (08威海)如图,点A,B在直线MN上,AB=11厘米,⊙A,⊙B的半径均为1厘米.⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(厘米)与时间t(秒)之间的关系式为r=1+t(t≥0).
 (1)试写出点A,B之间的距离d(厘米)
(1)试写出点A,B之间的距离d(厘米)
与时间t(秒)之间的函数表达式;
(2)问点A出发后多少秒两圆相切?
4.(08云南)已知,⊙ 的半径为
的半径为 ,⊙
,⊙ 的半径为
的半径为 ,且⊙
,且⊙ 与⊙
与⊙ 相切,则这两圆的圆心距为___________.
相切,则这两圆的圆心距为___________.
3.(08自贡)如图,⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=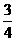 ,则弦AC的长为
.
,则弦AC的长为
.
2.(08赤峰) 如图,⊙O1,⊙O2,⊙O3两两相外切,⊙O1的半径 ,⊙O2的半
,⊙O2的半
 径
径 ,⊙O3的半径
,⊙O3的半径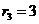 ,则
,则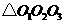 是( )
是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形或钝角三角形
1.(08长沙)如图,P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则sin∠APO
 等于( )
等于( )
A. B.
B.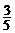
C. D.
D.
7. 与三角形各边都相切的圆叫做三角形的 ,内切圆的圆心是三角形 的交点,叫做三角形的 .
[典例精析]
例1 (08南平)如图,线段 经过圆心
经过圆心 ,交⊙O于点
,交⊙O于点 ,点
,点 在⊙O上,连接
在⊙O上,连接 ,
,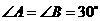 .
. 是⊙O的切线吗?请说明理由.
是⊙O的切线吗?请说明理由.

例2 (08湘潭)如图所示,⊙O的直径AB=4,点P是AB延长线上的一点,过P点作⊙O 的切线,切点为C,连结AC.
(1)若∠CPA=30°,求PC的长;
(2)若点P在AB的延长线上运动,∠CPA的平分线交AC于点M. 你认为∠CMP的大小是否发生变化?若变化,请说明理由;若不变化,求∠CMP的大小.

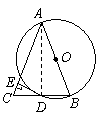 例3 (08恩施)如图,
例3 (08恩施)如图, 是⊙O的直径,
是⊙O的直径, 是⊙O的弦,延长
是⊙O的弦,延长 到点
到点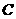 ,使
,使 ,连结
,连结 ,过点
,过点 作
作 ,垂足为
,垂足为 .
.
(1)求证: ;
;
(2)求证: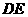 为⊙O的切线;
为⊙O的切线;
(3)若⊙O的半径为5, ,求
,求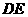 的长.
的长.
[中考演练]
6. 三角形的三个顶点确定 个圆,这个圆叫做三角形的外接圆,三角形的外接圆的圆心叫 心,是三角形 的交点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com