
题目列表(包括答案和解析)
7.梯形ABCD中,AD∥BC,AB=CD=AD=2,∠B=60°,则下底BC的长是(▲)
A.3
B.4 C.
2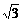 D.2+2
D.2+2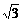
6.下列说法中正确的是(▲)
A.“打开电视,正在播放《新闻联播》”是必然事件;
B.某次抽奖活动中奖的概率为 ,说明每买100张奖券,一定有一次中奖;
,说明每买100张奖券,一定有一次中奖;
C.数据1,1,2,2,3的众数是3;
D.想了解台州市城镇居民人均年收入水平,宜采用抽样调查.
5.如图,⊙O的直径CD⊥AB,∠AOC=50°,则∠CDB大小为 (▲)
A.25° B.30° C.40° D.50°
4.下列运算正确的是(▲)
 A.
A. B.
B.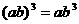 C.
C. D.
D.
3.如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,
则AP长不可能是(▲)
A.2.5 B.3 C.4 D.5
2.下列立体图形中,侧面展开图是扇形的是(▲)


1.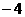 的绝对值是(▲)
的绝对值是(▲)
A.4
B. C.
C. D.
D.
26、如图1、在平面直角坐标系中,O是坐标原点,□ABCD的顶点A的坐标为(-2,0),点D的坐标为(0, ),点B在
),点B在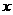 轴的正半轴上,点E为线段AD的中点,过点E的直线
轴的正半轴上,点E为线段AD的中点,过点E的直线 与
与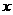 轴交于点F,与射线DC交于点G。
轴交于点F,与射线DC交于点G。
(1)求 的度数;
的度数;
(2)连结OE,以OE所在直线为对称轴,△OEF经轴对称变换后得到△ ,记直线
,记直线 与射线DC的交点为H。
与射线DC的交点为H。
①如图2,当点G在点H的左侧时,求证:△DEG∽△DHE;

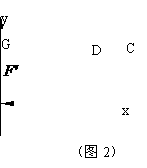
 ②若△EHG的面积为
②若△EHG的面积为 ,请直接写出点F的坐标。
,请直接写出点F的坐标。
25、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式。请你观察下列几种简单多面体模型,解答下列问题:

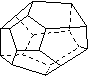


|
|
|
|
(1)根据上面多面体模型,完成表格中的空格:
|
多面体 |
顶点数(V) |
面数(F) |
棱数(E) |
|
四面体 |
4 |
7 |
|
|
长方体 |
8 |
6 |
12 |
|
正八面体 |
|
8 |
12 |
|
正十二面体 |
20 |
12 |
30 |
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______________。
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是____________。
(3)某个玻璃鉓品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为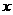 个,八边形的个数为
个,八边形的个数为 个,求
个,求 的值。
的值。
24、如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若 ,
, 。
。
(1)求⊙O的半径;
(2)求图中阴影部分的面积。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com