
题目列表(包括答案和解析)
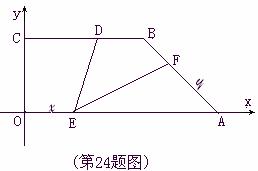
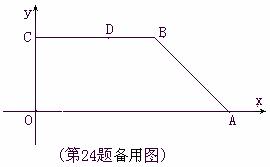
24.(12分)如图,直角梯形OABC的直角顶点O是坐标原点,边OA,OC分别在x轴、y轴的正半轴上,OA∥BC,D是BC上一点,BD= OA=
OA= ,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
(1)直接写出D点的坐标;
(2)设OE=x,AF=y,试确定y与x之间的函数关系;
(3)当△AEF是等腰三角形时,将△AEF沿EF折叠,得到△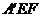 ,求△
,求△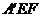 与五边形OEFBC重叠部分的面积.
与五边形OEFBC重叠部分的面积.
23.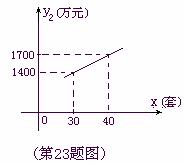 (10分)国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价
(10分)国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价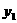 (万元)之间满足关系式
(万元)之间满足关系式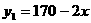 ,月产量x(套)与生产总成本
,月产量x(套)与生产总成本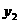 (万元)存在如图所示的函数关系.
(万元)存在如图所示的函数关系.
(1)直接写出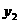 与x之间的函数关系式;
与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,
这种设备的利润W(万元)最大?最大利润是多少?
22. (8分)如图,⊙O的圆心在Rt△ABC的直角
(8分)如图,⊙O的圆心在Rt△ABC的直角
边AC上,⊙O经过C、D两点,与斜边AB交于
点E,连结BO、ED,有BO∥ED,作弦EF⊥AC
于G,连结DF.
(1)求证:AB为⊙O的切线;
(2)若⊙O的半径为5,sin∠DFE=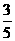 ,
,
求EF的长.
21.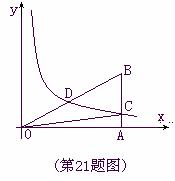 (8分)已知:关于x 的一元二次方程
(8分)已知:关于x 的一元二次方程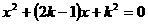 的两根
的两根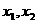 满足
满足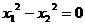 ,双曲线
,双曲线 (x>0)经过Rt△OAB斜边OB
(x>0)经过Rt△OAB斜边OB
的中点D,与直角边AB交于C(如图),求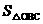 .
.
20.(8分)2010年,世博会在我国的上海举行,在网上随机调取了5月份中的某10天持票入园参观的人数,绘成下面的统计图.根据图中的信息回答下列问题:
(1)求出这10天持票入园人数的平均数、中位数和众数;
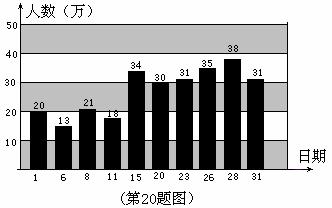 (2)不考虑其它因素的影响,以这10天的数据作为样本,估计在世博会开馆的184天中,持票入园人数超过
(2)不考虑其它因素的影响,以这10天的数据作为样本,估计在世博会开馆的184天中,持票入园人数超过
30万人的有多少天?
19.(7分)如图,将正方形ABCD中的△ABD绕对称中心O
旋转至△GEF的位置,EF交AB于M,GF交BD于N.请猜
想BM与FN有怎样的数量关系?并证明你的结论.
18.(7分)解方程: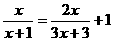
17. (6分)计算:
(6分)计算: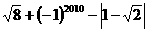
16.屏幕上有四张卡片,卡片上分别有大写的英文字母“A,Z,E,X”,现已将字母隐藏.只要用手指触摸其中一张,上面的字母就会显现出来.某同学任意触摸其中2张,上面显现的英文字母都是中心对称图形的概率是 .
15.
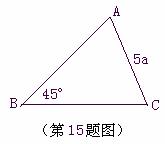 如图,在△ABC中,∠B=45°,cos∠C=
如图,在△ABC中,∠B=45°,cos∠C=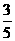 ,AC=5a,
,AC=5a,
则△ABC的面积用含a的式子表示是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com