
题目列表(包括答案和解析)
8.若 ,则
,则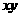 的值为
的值为
A.8 B. 2
C.5 D.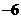
7.如图2,小明在扇形花台OAB沿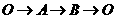 D路径散步,能近似地刻画小明到出发点O的距离y与时间x之间的函数图象是
D路径散步,能近似地刻画小明到出发点O的距离y与时间x之间的函数图象是

6.玉树地震后,某市人民献爱心为玉树捐人民币:203000000元,这个数用科学记数法表示为
A.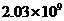 B.
B.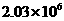 C.
C.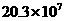 D.
D.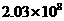
5.等腰三角形的两边长为4、9,则它的周长是
A.17 B.17或22 C.20 D.22
4.某同学午觉醒来发现钟表停了,他打开收音机想听电台整点报时,则他等待的时间不超过15分钟的概率是
A.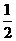 B.
B.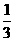 C.
C. D.
D.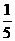
3.由四个相同的小正方体堆成的物体,如图l所示,它的俯视图是
2.下列计算正确的是
 A.
A.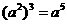 B.
B.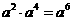 C.
C.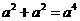 D.
D.
1.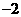 的绝对值是
的绝对值是
A.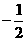 B.2 C.
B.2 C.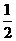 D.
D.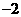
25.(本小题满分12分)
﹙1﹚①证明:分别过点M,N作 ME⊥AB,NF⊥AB,垂足分别为点E,F.
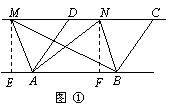 ∵ AD∥BC,AD=BC,
∵ AD∥BC,AD=BC,
∴ 四边形ABCD为平行四边形.
∴ AB∥CD.
∴ ME= NF.
∵ S△ABM=
S△ABM= ,S△ABN=
,S△ABN=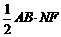 ,
,
∴ S△ABM= S△ABN. ……………………………………………………………………1分
②相等.理由如下:分别过点D,E作DH⊥AB,EK⊥AB,垂足分别为H,K.
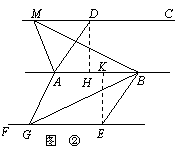 则∠DHA=∠EKB=90°.
则∠DHA=∠EKB=90°.
∵ AD∥BE,
∴ ∠DAH=∠EBK.
∵ AD=BE,
∴ △DAH≌△EBK.
∴ DH=EK. ……………………………2分
∵ CD∥AB∥EF,
∴ S△ABM=
S△ABM=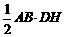 ,S△ABG=
,S△ABG= ,
,
∴ S△ABM= S△ABG. …………………………………………………………………3分
﹙2﹚答:存在. …………………………………………………………………………4分
解:因为抛物线的顶点坐标是C(1,4),所以,可设抛物线的表达式为 .
.
又因为抛物线经过点A(3,0),将其坐标代入上式,得 ,解得
,解得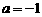 .
.
∴ 该抛物线的表达式为 ,即
,即 . ………………………5分
. ………………………5分
∴ D点坐标为(0,3).
设直线AD的表达式为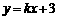 ,代入点A的坐标,得
,代入点A的坐标,得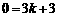 ,解得
,解得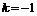 .
.
∴ 直线AD的表达式为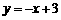 .
.
过C点作CG⊥x轴,垂足为G,交AD于点H.则H点的纵坐标为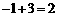 .
.
∴ CH=CG-HG=4-2=2. …………………………………………………………6分
设点E的横坐标为m,则点E的纵坐标为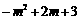 .
.
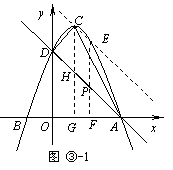
过E点作EF⊥x轴,垂足为F,交AD于点P,则点P的纵坐标为 ,EF∥CG.
,EF∥CG.
 由﹙1﹚可知:若EP=CH,则△ADE与△ADC的面积相等.
由﹙1﹚可知:若EP=CH,则△ADE与△ADC的面积相等.
①若E点在直线AD的上方﹙如图③-1﹚,
则PF=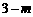 ,EF=
,EF=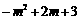 .
.
∴ EP=EF-PF=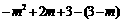 =
=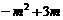 .
.
∴ 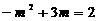 .
.
解得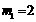 ,
,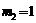 . ……………………………7分
. ……………………………7分
当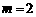 时,PF=3-2=1,EF=1+2=3.
时,PF=3-2=1,EF=1+2=3.
∴ E点坐标为(2,3).
同理 当m=1时,E点坐标为(1,4),与C点重合. ………………………………8分
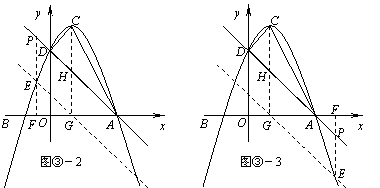
②若E点在直线AD的下方﹙如图③-2,③-3﹚,
则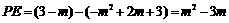 . ……………………………………………9分
. ……………………………………………9分
∴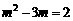 .解得
.解得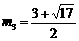 ,
,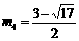 . ………………………………10分
. ………………………………10分
当 时,E点的纵坐标为
时,E点的纵坐标为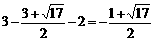 ;
;
当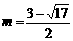 时,E点的纵坐标为
时,E点的纵坐标为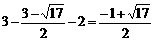 .
.
∴ 在抛物线上存在除点C以外的点E,使得△ADE与△ACD的面积相等,E点的坐标为E1(2,3);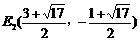 ;
;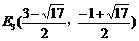 . ………………12分
. ………………12分
﹙其他解法可酌情处理﹚
24.(本小题满分11分)
(1)证明:由题意,知△ABC≌△A1B1C1,
∴ AB= A1B1,BC1=AC,∠2=∠7,∠A=∠1.
∴ ∠3=∠A=∠1. ………………………………………………………………1分
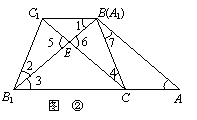 ∴ BC1∥AC.
∴ BC1∥AC.
∴ 四边形ABC1C是平行四边形. ………………2分
∴ AB∥CC1.
∴ ∠4=∠7=∠2. …………………………………3分
∵ ∠5=∠6,
∴ ∠B1C1C=∠B1BC.……………………………4分
﹙2﹚∠A1C1C =∠A1BC. …………………………5分
 理由如下:由题意,知△ABC≌△A1B1C1,
理由如下:由题意,知△ABC≌△A1B1C1,
∴ AB= A1B1,BC1=BC,∠1=∠8,∠A=∠2.
∴ ∠3=∠A,∠4=∠7. ………………………6分
∵ ∠1+∠FBC=∠8+∠FBC,
∴ ∠C1BC=∠A1BA. …………………………7分
∵ ∠4= (180°-∠C1BC),∠A=
(180°-∠C1BC),∠A= (180°-∠A1BA).
(180°-∠A1BA).
∴ ∠4=∠A. …………………………………8分
∴ ∠4=∠2.
∵ ∠5=∠6,
∴ ∠A1C1C=∠A1BC.……………………………………………………………………9分
﹙3﹚△C1FB,…………10分; △A1C1B,△ACB.…………11分﹙写对一个不得分﹚
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com