3．会用枚举法探求等可能事件的概率。会用区域面积之比解决简单的几何概型。

2．通过实例，体会概率的含义及其重要作用；在一些有趣的古典概率问题讨论中，感知其中蕴含的科学思想和文化。

1．在“分数”的学习中，引入“可能性”问题，学习用数量来描述一个事件发生的可能性大小，初步体会朴素的概率思想。

八年级第二学期：第二十三章　 概率初步(8课时)

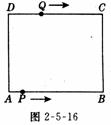
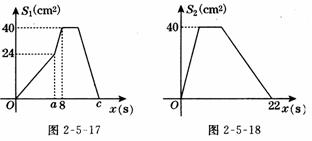
10. (10分)如图2－5-16，在矩形ABCD中，AB=10。cm，BC=8cm．点P从A出发，沿A→B→C→D路线运动，到D停止；点Q从D出发，沿D→C→B→A路线运动，到A停止，若点P、点Q同时出发，点P的速度为1cm/s，点Q的速度为2cm/s，a s时点P、点Q同时改变速度，点P的速度变为bcm/s，点Q的速度变为d cm/s，图 2－5－17是点 P出发x秒后△APD的面积S₁(cm²)与x(s)的函数关系图象；图2－5－18是点Q出发xs后面AQD的面积S₂(cm²)与x(s)的函数关系图象．

⑴ 参照图2－5－17，求a、b及图中c的值；

⑵ 求d的值；

⑶ 设点P离开点A的路程为y₁(cm)，点Q到点A还需走的路程为y₂(cm)，请分别写出动点 P、Q改变速度后，y₁、y₂与出发后的运动时间x(s)的函数解析式，并求出P、Q相遇时x的值．

⑷ 当点Q出发_______s时，点P、点Q在运动路线上相距的路程为25cm．

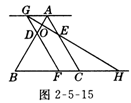
9．(10分)如图2－5－15所示，等边三角形ABC的边长为6，点D、E分别在边AB，AC上，且AD=AE=2，若点F从点B开始以每秒二个单位长度的速度沿射线BC方向运动，设点F运动的时间为t秒，当t＞0时，直线FD与过点A且平行于BC的直线相交于点G，GE的延长线与BC的延长线相交于点H，AB与GH相交于点O．

⑴ 设△EGA的面积为S，写出S与 t的函数解析式；

⑵ 当t为何值时，AB⊥GH；

⑶ 请你证明△GFH的面积为定值．

8．(10分)已知矩形ABCD在平面直角坐标系中，顶点A、B、D的坐标分别为A(0，0)，B(m，0)，D(0，4)其中m≠0．

⑴ 写出顶点C的坐标和矩形ABCD的中心P点的坐标(用含m的代数式表示)

⑵ 若一次函数y=kx－1的图象把矩形ABCD分成面积相等的两部分，求此一次函数的解析式(用含m的代数式表示)

⑶ 在⑵的前提下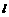，又与半径为1的⊙M相切，且点　 M(0，1)，求此矩形ABCD的中心P点的坐标．

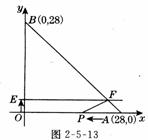
7．(12分)如图2－5－14所示，在直角坐标系中，矩形ABCD的顶点，A的坐标为(1，0)，对角线的交点P的坐标为(，1)

⑴ 写出B、C、D三点的坐标；

⑵ 若在AB上有一点 E作，’入过　 E点的直线‘将矩形ABCD的面积分为相等的两部分，求直线l的解析式；

⑶ 若过C点的直线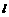将矩形ABCD的面积分为4：3两部分，并与y轴交于点M，求过点C、D、M三点的抛物线的解析式．

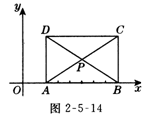
6．(12分)如图2－5－13所示，已知A由两点坐标分另为(28，0)和(0，28)，动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动，动直线 EF从 x轴开始以每秒1个长度单位的速度向上平行移动(即EF∥x轴)并且分别交y轴，线段AB交于E、F点．连接FP，设动点P与动直线EF同时出发，运动时间为t秒．

⑴ 当t＝1秒时，求梯形OPFE的面积，t为何值时，梯形OPFE的面积最大，最大面积是多少？

⑵ 当梯形OPFE的面积等于△APF的面积时，求线段　 PF的长．

⑶ 设t的值分别取t₁，t₂时(t₁≠t₂)，所对应的三角形分别为△AF₁P₁和△AF₂P₂ ，试判断这两个三角形是否相似，请证明你的判断．

5．(10分)如图2－5-12所示，已知等边三角形ABC中，AB=2，点P是AB边上的任意一点(点P可以与点A重合，但不与点B重合)，过点P作PE⊥BC．垂足为E；过点E作EF⊥AC，垂足为F；过点F作FQ⊥AB，垂足为Q．设BP=x，AQ=y．

⑴ 写出y与x之间的函数关系式；

⑵ 当BP的长等于多少时，点P与点Q重合；

⑶ 当线段 PE、FQ相交时，写出线段PE、EF、FQ所围成三角形的周长的取值范围(不必写出解题过程)