
题目列表(包括答案和解析)
八年级第二学期:第二十章 一次函数(9课时)
28.已知:如图,函数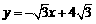 的图象与x轴相交于点A,与函数
的图象与x轴相交于点A,与函数 的图象相交于点P.
的图象相交于点P.
(1)求点P的坐标.
(2)请判断 的形状并说明理由.
的形状并说明理由.
 (3)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
(3)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:① S与t之间的函数关系式.
② 当t为何值时,S最大,并求S的最大值.
27.某水产品养殖企业为指导该企业某种水产品的养殖和销售,对历年市场行情和水产品养殖情况进行了调查.调查发现这种水产品的每千克售价 (元)与销售月份
(元)与销售月份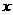 (月)满足关系式
(月)满足关系式 ,而其每千克成本
,而其每千克成本 (元)与销售月份
(元)与销售月份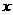 (月)满足的函数关系如图所示.
(月)满足的函数关系如图所示.
(1)试确定 的值;
的值;
(2)求出这种水产品每千克的利润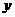 (元)与销售月份
(元)与销售月份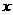 (月)之间的函数关系式;
(月)之间的函数关系式;
(3)“五·一”之前,几月份出售这种水产品每千克的利润最大?最大利润是多少?

26.如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
实验与探究:
 (1)由图观察易知A(0,2)关于直线l的对称点
(1)由图观察易知A(0,2)关于直线l的对称点 的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线l的对称点
的坐标为(2,0),请在图中分别标明B(5,3) 、C(-2,5) 关于直线l的对称点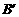 、
、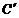 的位置,并写出它们的坐标:
的位置,并写出它们的坐标: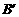 、
、 ;
;
归纳与发现:
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点 的坐标为 .
的坐标为 .
(不必证明);
运用与拓广:
(3)已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
25.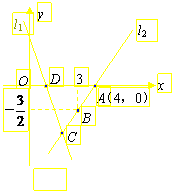 如图,直线
如图,直线 的函数表达式为
的函数表达式为 ,且
,且 与
与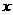 轴交于点
轴交于点 ,直线
,直线 经过点
经过点 ,直线
,直线 ,
, 交于点
交于点 .
.
(1)求点 的坐标;
的坐标;
(2)求直线 的函数表达式;
的函数表达式;
(3)求 的面积;
的面积;
(4)在直线 上存在异于点
上存在异于点 的另一点
的另一点 ,使得
,使得
|
 的面积相等,请直接写出点
的面积相等,请直接写出点 的坐标.
的坐标.24.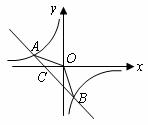 如图,已知
如图,已知 ,
, 是一次函数
是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线 与
与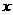 轴的交点
轴的交点 的坐标及△
的坐标及△ 的面积;
的面积;
(3)求方程 的解(请直接写出答案);
的解(请直接写出答案);
|
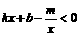 的解集(请直接写出答案).
的解集(请直接写出答案).23.鞋子的“鞋码”和鞋长(cm)存在一种换算关系,下表是几组“鞋码”与鞋长换算的对应数值:[注:“鞋码”是表示鞋子大小的一种号码]
|
鞋长(cm) |
16 |
19 |
21 |
24 |
|
鞋码(号) |
22 |
28 |
32 |
38 |
(1)设鞋长为x,“鞋码”为y,试判断点(x,y)在你学过的哪种函数的图象上?
(2)求y与 x之间的函数关系式;
(3)如果某人穿44号“鞋码”的鞋,那么他的鞋长是多少?
22.杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端B处,其身体(看成一点)的路线是二次函数 图象的一部分,如图.
图象的一部分,如图.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.

|
||||
|
||||
 |
21.人的视觉机能受运动速度的影响很大,行驶中司机在驾驶室内观察前方物体时是动态的,
车速增加,视野变窄。当车速为50km/h时,视野为80度。如果视野f(度)是车速v(km/h)
的反比例函数,求f,v之间的关系式,并计算当车速为100 km/h时视野的度数.
20.如图,点 、
、 是函数
是函数 的图象上的点,分别经过
的图象上的点,分别经过 、
、 两点向
两点向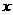 轴、
轴、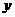 轴作垂线段,若
轴作垂线段,若 则
则 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com