
题目列表(包括答案和解析)
例1: 已知:x2+y2+4x-6y+13=0,x、y均为有理数,求xy的值。
分析:逆用完全乘方公式,将
x2+y2+4x-6y+13化为两个完全平方式的和,利用完全平方式的非负性求出x与y的值即可。
解:∵x2+y2+4x-6y+13=0,
(x2+4x+4)+(y2-6y+9)=0,
即(x+2)2+(y-3)2=0。
∴x+2=0,y=3=0。
即x=-2,y=3。
∴xy=(-2)3=-8。

分析:本题巧妙地利用

例3 已知:a+b=8,ab=16+c2,求(a-b+c)2002的值。
分析:由已知条件无法直接求得(a-b+c)2002的值,可利用(a-b)2=(a+b)2-4ab确定a-b与c的关系,再计算(a-b+c)2002的值。
解:(a-b)2=(a+b)2-4ab=82-4(16+c2)=-4c2。
即:(a-b)2+4c2=0。
∴a-b=0,c=0。
∴(a-b+c)2002=0。
例4 已知:a、b、c、d为正有理数,且满足a4+b4+C4+D4=4abcd。
求证:a=b=c=d。
分析:从a4+b4+C4+D4=4abcd的特点看出可以化成完全平方形式,再寻找证明思路。
证明:∵a4+b4+C4+D4=4abcd,
∴a4-2a2b2+b4+c4-2c2d2+d4+2a2b2-4abcd+2c2d2=0,
(a2-b2)2+(c2-d2)2+2(ab-cd)2=0。
a2-b2=0,c2-d2=0,ab-cd=0
又∵a、b、c、d为正有理数,
∴a=b,c=d。代入ab-cd=0,
得a2=c2,即a=c。
所以有a=b=c=d。
练习:
1. 已知:x2+3x+1=0。

a2+b2=(a+b)2-2ab,
a2+b2=(a-b)2+2ab,
(a+b)2-(a-b)2=4ab,
a2+b2+c2=(a+b+c)2-2(ab+ac+bc)
19、(08年荆州)“5•12”汶川大地震后,某健身器材销售公司通过当地“红十字会”向灾区献爱心,捐出了五月份全部销售利润.已知该公司五月份只售出甲、乙、丙三种型号器材若干台,每种型号器材不少于8台,五月份支出包括这批器材进货款64万元和其他各项支出(含人员工资和杂项开支)3.8万元.这三种器材的进价和售价如下表,人员工资y1(万元)和杂项支出y2(万元)分别与总销售量x(台)成一次函数关系(如图).
(1)求y1与x的函数解析式;
(2)求五月份该公司的总销售量;
(3)设公司五月份售出甲种型号器材t台,五月份总销售利润为W(万元),求W与t的函数关系式;(销售利润=销售额-进价-其他各项支出)
 (4)请推测该公司这次向灾区捐款金额的最大值.
(4)请推测该公司这次向灾区捐款金额的最大值.
|
型 号 |
甲 |
乙 |
丙 |
|
进价(万元/台) |
0.9 |
1.2 |
1.1 |
|
售价(万元/台) |
1.2 |
1.6 |
1.3 |
(06资阳)某乒乓球训练馆准备购买n副某种品牌的乒乓球拍,每副球拍配k(k≥3)个乒乓球。 已知A、B两家超市都有这个品牌的乒乓球拍和乒乓球出售,且每副球拍的标价都为20元,每个乒乓球的标价都为1元 。现两家超市正在促销,A超市所有商品均打九折(按原价的90%付费)销售,而B超市买1副乒乓球拍送3个乒乓球 。 若仅考虑购买球拍和乒乓球的费用,请解答下列问题:
(1)如果只在某一家超市购买所需球拍和乒乓球,那么去A超市还是B超市买更合算?
(2) 当k=12时,请设计最省钱的购买方案.
解:(1) 由题意,去A超市购买n副球拍和kn个乒乓球的费用为0.9(20n+kn)元,去B超市购买n副球拍和kn个乒乓球的费用为[20n+ n(k-3)]元,
由0.9(20n+kn)< 20n+ n (k-3),解得 k>10;
由0.9(20n+kn)= 20n+n (k-3),解得 k=10;
由0.9(20n+kn)> 20n+n (k-3),解得 k<10.
∴ 当k>10时,去A超市购买更合算;当k=10时,去A、B两家超市购买都一样;当3≤k<10时,去B超市购买更合算.
(2) 当k=12时,购买n副球拍应配12n个乒乓球.
若只在A超市购买,则费用为0.9(20n+12n)=28.8n(元);
若只在B超市购买,则费用为20n+(12n-3n)=29n(元);
设在B超市购买x副球拍,在A超市购买(n-x) 副球拍,然后再在A超市购买不足的乒乓球,
则费用y=20n+18n×0.9+0.9×(12n-3x) =-0.7x+28.8n.由一次函数的增减性可知,当x=n时,y最小.miny=28.1n
显然,28.1n<28.8n <29n.
∴ 最省钱的购买方案为:在B超市购买n副球拍同时获得送的3n个乒乓球,然后在A超市按九折购买9n个乒乓球.
(07潜江)工业园区某消毒液工厂,今年四月份以前,每天的产量与销售量均为500箱.进入四月份后,每天的产量保持不变,市场需求量不断增加.如图是四月前后一段时期库存量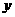 (箱)与生产时间
(箱)与生产时间 (月份)之间的函数图象.
(月份)之间的函数图象.
(1)四月份的平均日销售量为多少箱?
(2)该厂什么时候开始出现供不应求的现象,此时日销售量为多少箱?
(3)为满足市场需求,该厂打算在投资不超过135万元的情况下,购买5台新设备,使扩大生产规模后的日产量不低于四月份的平均日销售量.现有A、B两种型号的设备可供选择,其价格与两种设备的日产量如下表:
请问:有哪几种购买设备的方案?若为了使日产量最大,应选择哪种方案?
|
型
号 |
A |
B |
|
价格(万元/台) |
28 |
25 |
|
日产量(箱/台) |
50 |
40 |
某垦荒队安排30 个劳动力开垦出75亩土地,这些土地可以种蔬菜、水稻和地瓜,如果种这些农作物所需的劳动力和预计的产值如下表:
|
|
蔬菜 |
水稻 |
地瓜 |
|
每亩所需劳动力(人) |
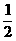 |
 |
 |
|
每亩预计的产值(元) |
100 |
70 |
45 |
设蔬菜、水稻、地瓜的土地分别为x亩、y亩、z亩,预计总产值为A元,要求使所有土地都种上农作物,全部劳动力都有工作.
请用x分别表示y和z;
(1) 请写出A与x之间的函数关系式,并求出自变量x的取值范围;
(2) 现要求农作物预计总产值达到最高,请你说出合理的种植方案.
如图,直线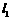 的解析表达式为
的解析表达式为 ,且
,且 与x轴交于点B(-1,0),与y轴交于点D.l
与x轴交于点B(-1,0),与y轴交于点D.l 与y轴的交点为C(0,-2),直线l
与y轴的交点为C(0,-2),直线l 、l
、l 相交于点A,结合图像解答下列问题:
相交于点A,结合图像解答下列问题:
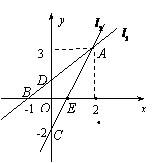 (1)求△ADC的面积;
(1)求△ADC的面积;
(2)求直线l 表示的一次函数的解析式;
表示的一次函数的解析式;
(3)当x为何值时,l 、l
、l 表示的两个函数的函数值都大于0.
表示的两个函数的函数值都大于0.
(08巴中市)为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量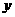 (mg)与燃烧时间
(mg)与燃烧时间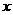 (分钟)成正比例;燃烧后,
(分钟)成正比例;燃烧后,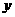 与
与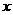 成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
 (1)求药物燃烧时
(1)求药物燃烧时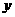 与
与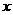 的函数关系式.
的函数关系式.
(2)求药物燃烧后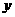 与
与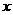 的函数关系式.
的函数关系式.
(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?
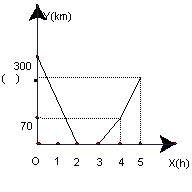 北京市与石家庄市两地相距300km,甲车在北京市,乙车在石家庄市,两车同时出发,相向而行,在A地相遇。为节约费用(两车相遇并换货后,均需按原路返回出发地)。两车换货后,甲车立即按原路返回北京市,而乙车又停留1小时后按原路返回石家庄市。设每车在行驶过程中速度保持不变,两车间的距离y(km)与时间x(h)的函数关系如图10所示,根据所提供的信息,回答下列问题:
北京市与石家庄市两地相距300km,甲车在北京市,乙车在石家庄市,两车同时出发,相向而行,在A地相遇。为节约费用(两车相遇并换货后,均需按原路返回出发地)。两车换货后,甲车立即按原路返回北京市,而乙车又停留1小时后按原路返回石家庄市。设每车在行驶过程中速度保持不变,两车间的距离y(km)与时间x(h)的函数关系如图10所示,根据所提供的信息,回答下列问题:
(1)①两车从出发开始到A地相遇用了_______h;②两车在A地换货用了_____h;③甲车的速度是______km/h,乙车的速度是______km/h;④在图中y轴上的小括号内应填的数字是______.
(2)从两车开始同时出发到4.6h时,甲车与乙车相距多少千米?
(桥西模拟)如图,反映的是甲、乙两人以每分钟80米的速度从公司出发步行到火车站乘车的过程。再去火车站的途中,甲忽然发现忘带预购的车票,立刻以同样的速度返回,然后乘坐出租车赶往火车站,途中与乙相遇后,带上乙一同到火车站,结果到火车站的时间比预计步行到火车站的时间早到了3分钟。
(1)甲离开公司 分钟发现忘记带车票;甲、乙预计步行到火车站时路程s与时间t的函数解析式为 。
(2)求图中出租车行驶路程与时间t的函数关系式。
(3)出租车的速度与公司到火车站的路程各是多少?
18、 (深圳08)“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
17、(重庆07)我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售。按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满。根据下表提供的信息,解答以下问题:
(1)设装运A种脐橙的车辆数为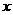 ,装运B种脐橙的车辆数为
,装运B种脐橙的车辆数为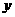 ,求
,求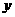 与
与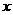 之间的函数关系式;
之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值。
16、(河北07)一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,每款手机至少要购进8部,且恰好用完购机款61000元.设购进A型手机x部,B型手机y部.三款手机的进价和预售价如下表:
|
手机型号 |
A型 |
B型 |
C型 |
|
进 价(单位:元/部) |
900 |
1200 |
1100 |
|
预售价(单位:元/部) |
1200 |
1600 |
1300 |
(1)用含x,y的式子表示购进C型手机的部数;
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
|
脐 橙 品 种 |
A |
B |
C |
|
每辆汽车运载量(吨) |
6 |
5 |
4 |
|
每吨脐橙获利(百元) |
12 |
16 |
10 |
15、(重庆08)为支持四川抗震救灾,重庆市A、B、C三地现在分别有赈灾物资100吨,、100吨、80吨,需要全部运往四川重灾地区的D、E两县。根据灾区的情况,这批赈灾物资运往D县的数量比运往E县的数量的2倍少20吨。
(1)求这批赈灾物资运往D、E两县的数量各是多少?
(2)若要求C地运往D县的赈灾物资为60吨,A地运往D的赈灾物资为x吨(x为整数),B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍。其余的赈灾物资全部运往E县,且B地运往E县的赈灾物资数量不超过25吨。则A、B两地的赈灾物资运往D、E两县的方案有几种?请你写出具体的运送方案;
(3)已知A、B、C三地的赈灾物资运往D、E两县的费用如下表:
|
|
A地 |
B地 |
C地 |
|
运往D县的费用(元/吨) |
220 |
200 |
200 |
|
运往E县的费用(元/吨) |
250 |
220 |
210 |
为及时将这批赈灾物资运往D、E两县,某公司主动承担运送这批赈灾物资的总费用,在(2)问的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?
14、(07聊城市)某市为了进一步改善居民的生活环境,园林处决定增加公园 和公园
和公园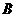 的绿化面积.已知公园
的绿化面积.已知公园 分别有如图14--1,图14--2所示的阴影部分需铺设草坪,其中图14--2所示的阴影部分的面积为1008
分别有如图14--1,图14--2所示的阴影部分需铺设草坪,其中图14--2所示的阴影部分的面积为1008 .在甲、乙两地分别有同种草皮
.在甲、乙两地分别有同种草皮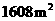 和
和 出售,且售价一样.若园林处向甲、乙两地购买草皮,其路程和运费单价见下表:
出售,且售价一样.若园林处向甲、乙两地购买草皮,其路程和运费单价见下表:
|
|
公园 |
公园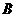 |
||
|
路程(千米) |
运费单价(元) |
路程(千米) |
运费单价(元) |
|
|
甲地 |
 |
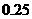 |
 |
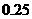 |
|
乙地 |
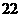 |
 |
 |
 |
(注:运费单价指将每平方米草皮运送1千米所需的人民币)

(1)求出公园A(图25--1)需铺设草坪的面积;
(2)设总运费为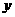 (元),公园
(元),公园 向甲地购买草皮
向甲地购买草皮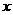 (
(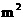 ),求出
),求出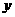 与
与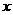 之间的函数关系式;
之间的函数关系式;
(3)请设计出总运费最省的草皮运送方案,并说明理由.
13、(08沈阳)一辆经营长途运输的货车在高速公路的 处加满油后,以每小时80千米的速度匀速行驶,前往与
处加满油后,以每小时80千米的速度匀速行驶,前往与 处相距636千米的
处相距636千米的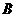 地,下表记录的是货车一次加满油后油箱内余油量
地,下表记录的是货车一次加满油后油箱内余油量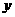 (升)与行驶时间
(升)与行驶时间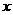 (时)之间的关系:
(时)之间的关系:
行驶时间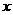 (时) (时) |
0 |
1 |
2 |
2.5 |
余油量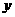 (升) (升) |
100 |
80 |
60 |
50 |
(1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示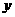 与
与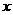 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
(2)按照(1)中的变化规律,货车从 处出发行驶4.2小时到达
处出发行驶4.2小时到达 处,求此时油箱内余油多少升?
处,求此时油箱内余油多少升?
(3)在(2)的前提下, 处前方18千米的
处前方18千米的 处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在
处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在 处至少加多少升油,才能使货车到达
处至少加多少升油,才能使货车到达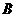 地.(货车在
地.(货车在 处加油过程中的时间和路程忽略不计)
处加油过程中的时间和路程忽略不计)
12、(08辽宁)2008年6月1日起,我国实施“限塑令”,开始有偿使用环保购物袋.为了满足市场需求,某厂家生产 两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产
两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产 种购物袋
种购物袋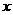 个,每天共获利
个,每天共获利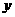 元.
元.
|
|
成本(元/个) |
售价(元/个) |
 |
2 |
2.3 |
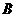 |
3 |
3.5 |
(1)求出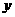 与
与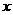 的函数关系式;
的函数关系式;
(2)如果该厂每天最多投入成本10000元,那么每天最多获利多少元?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com