
题目列表(包括答案和解析)
1. 下列各组数中,相等的是_________
A.  和1 B.
和1 B.  和-1 C.
和-1 C.  和-1 D.
和-1 D.

(五)代数式的化简求值
含有绝对值的代数式的化简,通常可利用数轴的直观性;整式的化简求值常常要灵活运用配方法、换元法、整体代换思想和构造思想;分式的化简求值一般可对分子、分母的多项式因式分解、约分。再运用分式的性质化简计算;二次根式的化简求值一般应先考虑能否利用二次根式的性质,配方法、乘法公式等化简计算。
[典型例题]
例1. 在
A. 1 B. 2 C. 3 D. 4
分析:应当知道,只有无限不循环的小数才是无理数,有限小数0.80108,无限循环小


例2. 已知下列5个命题
(1)零是最小的实数
(2)数轴上所有的点都表示实数
(3)两个无理数的和仍然是无理数

(5)任何实数都有两个互为相反数的平方根
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
分析:(1)要正确区分实数的最小值和实数绝对值最小值的意义
(2)要正确区分平方根和立方根的相同点和不同点
(3)“任何数……”就意味着没有例外,因此若能举出一个反例便可证明原命题是假命题。
因此可以得出5个命题中只有(2)是真命题,故选A。
例3. 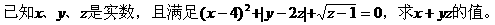
解:





注意:这是一个条件求值问题,利用非负数的性质可以求出x、y、z的值,从而使问题得解。
例4. 
解:



归纳:
其中a≠0,P是正整数,在本题中,
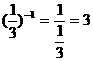

例5. 
的值为( )
解:

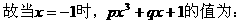

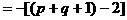

例6. 
解: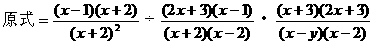


归纳:对分子、分母都是多项式的分式进行乘除运算时,一定要先将每个多项式分解因式,然后将除法统一成乘法,最后再进行约分化简。
实战演练
(四)代数式的恒等变形
添括号、去括号、拆项是代数式恒等变形的常用方法,乘法公式、因式分解是代数式恒等变形的工具。待定系数法、配方法也都可进行代数式的恒等变形。
(三)和代数式有关的概念及代数式的运算。
(1)代数式的分类

(2)各类代数式的概念
单项式、多项式、整式、分式、有理式、无理式、根式、二次根式、最简二次根式、同类二次根式。
(3)代数式有意义的条件:
分式有意义的条件是分母不为零
分式的值为零的条件是分母不为零,分子为零二次根式有意义的条件是被开方数(式)非负,由实际应用中得到的代数式还要符合实际意义。
(4)代数式的运算:
整式的加、减、乘、除运算及添括号、去括号法则。
分式的加、减、乘、除运算及分式的乘方。
二次根式的加、减、乘、除运算及二次根式的分母有理化。
(二)实数的运算
实数的六种运算及整数指数幂的运算是初中学习数学的基本能力,也是后续学习的重要基础。准确的运算有赖于运算法则、运算顺序和运算律的熟练掌握。
(一)实数的有关概念
(1)实数的分类

当然还可以分为:正实数、零、负实数。
有理数还可以分为:正有理数,零,负有理数
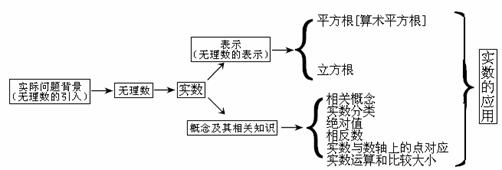


(2)数轴:
数轴是研究实数的重要工具,是在数与式的学习中,实现数形结合的载体,数轴的三要素:原点、正方向和单位长度,实数与数轴上的点是一、一对应的,这种一一对应关系是数学中数形结合的重要基础,我们还可以利用这种一、一对应关系来比较两个实数的大小。
(3)绝对值

绝对值的几何意义:一个数的绝对值是这个数在数轴上的对应点到原点的距离。
(4)相反数、倒数

若a、b两个数为互为相反数,则a+b=0。
若m、n两个数互为倒数,则m·n=1。
(5)三种非负数:

“几个非负数的和(积)仍是非负数”与“几个非负数的和等于零,则必定每个非负数都同时为零”的结论常用于化简,求值。
(6)平方根、算术平方根、立方根的概念。
(7)科学计数法、有效数字和近似值的概念。
10、(1)由题意,得△DEF∽△CGF,
∴ ,∴FC=40(cm).
,∴FC=40(cm).
(2)如图,设矩形顶点B所对顶点为P,则
①当顶点P在AE上时,x=60,
y的最大值为60×30=1 800(cm2).
②当顶点P在EF上时,过点P分别作PN⊥BG于点N,PM⊥AB于点M.
根据题意,得△GFC∽△GPN.
∴ .∴NG=
.∴NG=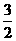 x,∴BN=120-
x,∴BN=120-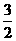 x.
x.
∴y=x(120-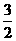 x)=-
x)=-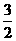 (x-40)2+2 400.
(x-40)2+2 400.
∴当x=40时,y的最大值为2 400(cm2).
③当顶点P在FC上时,y的最大值为60×40=2 400(cm2).
综合①②③,得x=40cm时,
矩形的面积最大,最大面积为2 400cm2.
(3)根据题意,正方形的面积y(cm2)与边长x(cm)满足的函数表达式为:
y=-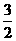 x2+120x.
x2+120x.
当y=x2时,正方形的面积最大.
∴x2=-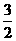 x2+120x.
x2+120x.
解之,得x1=0(舍去),x2=48(cm).
∴面积最大的正方形的边长为48cm.
10、(陕西)王师傅有两块板材边角料,其中30cm,下底为一块是边长为60cm的正方形板子;另一块是上底为30cm,下底为120cm,高为60cm的直角梯形板子(如图①).王师傅想将这两块板子裁成两块全等的矩形板材.他将两块板子叠放在一起,使梯形的两个直角顶点分别与正方形的两个顶点重合,两块板子的重叠部分为五边形ABCFE围成的区域(如图②).由于受材料纹理的限制,要求裁出的矩形要以点B为一个顶点.
(1)求FC的长;
(2)利用图②求出矩形顶点B所对的顶点到BC边的距离x(cm)为多少时,矩形的面积y(cm2)最大?最大面积是多少?
(3)若想使裁出的矩形为正方形,试求出面积最大的正方形的边长.

例2、[解题分析]⑴ 由 和
和
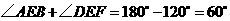 得
得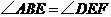 .
.
从而可得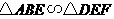

 与
与 的函数表达式是
的函数表达式是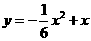
解:(1) (或
(或 )····················································· 3分
)····················································· 3分
(2) ,又
,又
 ····································································································· 5分
····································································································· 5分
 ,即
,即 ······························· 6分
······························· 6分
 ,
, ,
, ,
,
解得 ································································ 7分
································································ 7分
 梯形
梯形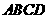 的中位线长为
的中位线长为 ······································································· 8分
······································································· 8分
9:分析:(1)当三角形QAP为等腰三角形时,由于∠A为直角,只能是AQ=AP,建立等量关系, ,即
,即 时,三角形QAP为等腰三角形;
时,三角形QAP为等腰三角形;
(2)四边形QAPC的面积=ABCD的面积-三角形QDC的面积-三角形PBC的面积
= =36,即当P、Q运动时,四边形QAPC的面积不变。
=36,即当P、Q运动时,四边形QAPC的面积不变。
(3)显然有两种情况:△PAQ∽△ABC,△QAP∽△ABC,
由相似关系得 或
或 ,解之得
,解之得 或
或
8、 (2007长沙)如图,□
(2007长沙)如图,□ 中,
中, ,
, ,
,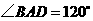 ,
, 为
为 上一动点(不与
上一动点(不与 重合),作
重合),作 于
于 ,
, ,
, 的延长线交于点
的延长线交于点 ,设
,设 ,
, 的面积为
的面积为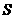 .
.
(1)求证: ;
;
(2)求用 表示
表示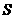 的函数表达式,并写出
的函数表达式,并写出 的取值范围;
的取值范围;
(3)当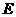 运动到何处时,
运动到何处时,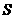 有最大值,最大值为多少?
有最大值,最大值为多少?
 9:如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动。如果P、Q同时出发,用t秒表示移动的时间(0≤ t ≤6),那么:
9:如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动。如果P、Q同时出发,用t秒表示移动的时间(0≤ t ≤6),那么:
(1)当t为何值时,三角形QAP为等腰三角形?
(2)求四边形QAPC的面积,提出一个与计算结果有关的结论。(变式:当点P、Q运动时,四边形QAPC的面积是否改变?若不变,求出它的面积;若改变,请说明理由。)
(3)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似。
7、如图5,△ABC内接于⊙O,D是弧AC的中点
求证:CD2=DE·DB。
|

C组
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com