
题目列表(包括答案和解析)
23. [改编] (本小题满分10分)
[改编] (本小题满分10分)
数形结合作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,即 “以数解形”;或者借助形的几何直观性来阐明数之间的某种关系,即 “以形助数”。
 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
(1)请你用数形结合的“以数解形”思想来解:如图2,已知在△ABC中(AC>BC),∠ACB=900,CD⊥AB,D为垂足, CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根,求AD、MD的长。
(2)请你用数形结合的“以形助数”思想来解: 设a、b、c、d都是正数,满足a:b=c:d,且a最大。求证:a+d>b+c(提示:不访设AB=a,CD=d,AC=b,BC=c,构造图1)
22.[改编] (本小题满分10分)
 2011年3月11日13时46分日本发生了9.0级大地震,伴随着就是海啸。山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。
2011年3月11日13时46分日本发生了9.0级大地震,伴随着就是海啸。山坡上有一棵与水平面垂直的大树,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。
已知山坡的坡角∠AEF=23°,量得树干的倾斜角为
∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m。
(1)求∠DAC的度数;
(2)求这棵大树折点C到坡面AE的距离?
|
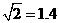 ,
, ,
,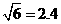 ).
).21.[改编](本小题满分8分)
“6”字形图中,FM是大⊙O的直径,BC与大⊙O相切于B,
OB与小⊙O相交于点A,AD∥BC,CD∥BH∥FM,DH⊥BH于H,
设∠FOB=α,OB=4,BC=6.
(1)求证:AD为小⊙O的切线;
|
(3)当α=30º时,求DH的长。(结果保留根号)
20. [改编](本小题满分8分)
2011年3月16日上午10时福岛第一核电站第3号反应堆发生了爆炸。为了抑制核辐射进一步扩散,日本决定向6号反应堆注水冷却,铀棒被放在底面积为100m2、高为20m的长方体水槽中的一个圆柱体桶内,如图(1)所示,向桶内注入流量一定的水,注满后,继续注水,直至注满水槽为止(假设圆柱体桶在水槽中的位置始终不改变)。水槽中水面上升的高度h与注水时间t之间的函数关系如图(2)所示。
(1)求圆柱体的底面积;(2)若的圆柱体高为9m,求注水的速度及注满水槽所用时间。
 h(cm)
h(cm)
 20
20

|
19.[改编](本小题满分6分)
端午节吃粽子是中华民族的传统习俗,五月初五早上,奶奶为小明准备了四只粽子:一
只 肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同。小明喜欢
肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同。小明喜欢
吃红枣馅的粽子。
(1)请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率;
(2)在吃粽子之前,小明准备用一格均匀的正四面体骰子(如图所示)
进行吃粽子的模拟试验,规定:掷得点数1向上代表肉馅,点数2向上代
表香肠馅,点数3, 向上代表红枣馅,连续抛掷这个骰子两次表示随机
向上代表红枣馅,连续抛掷这个骰子两次表示随机
吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率。你认为这样模拟正确吗?试说明理由。
18. [原创](本小题满分6分)
 (1)画图,已知线段a和锐角
(1)画图,已知线段a和锐角 ,求作Rt△ABC,使它的一边为a,一锐角为
,求作Rt△ABC,使它的一边为a,一锐角为 (不写作法,要保留作图痕迹,作出其中一个满足条件的直角三角形即可)。
(不写作法,要保留作图痕迹,作出其中一个满足条件的直角三角形即可)。
(2)回答问题:
1满足上述条件的大小不同的共有 种。
|
 =
= ,求最大的Rt△ABC的面积。
,求最大的Rt△ABC的面积。解答应写出文字说明、证明过程或推演步骤。如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以。
17. [原创](本小题满分6分)
[原创](本小题满分6分)
能否在图中的四个圆圈内填入4个互不相同的数,使得任意两个圆圈中所填的数的平方和等于另外两个圆圈中所填数的平方和?如果能填,请填出一个例;如果不能填,请说明理由。
|
16.
 [改编]如图,
[改编]如图, 、
、 分别是
分别是  的边
的边 、
、 上
上
的点, 与
与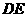 相交于点
相交于点 ,
, 与
与 相交于
相交于
点 ,若
,若 △APD
△APD 
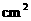 ,
, △BQC
△BQC 
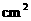 ,
,
则阴影部分的面积为
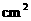 。
。
15.[改编]由于人民生活水平的不断提高,购买理财产品成为一个热门话题。某银行销售A,B,C三种理财产品,在去年的销售中,稳健理财产品C的销售金额占总销售金额的40% 。由于受国际金融危机的影响,今年A,B两种理财产品的销售金额都将比去年减少20%,因而稳健理财产品C是今年销售的重点。若要使今年的总销售金额与去年持平,那么今年稳健理财产品C的销售金额应比去年增加 %
13.[原创]已知关于x的一元二次方程 有解,求k的取值范围
。
有解,求k的取值范围
。
14.[原创]刘谦的魔术表演风靡全国,小明也学起了刘谦发明了一个魔术盒,当任意实数对(a,b)进入其中时,会得到一个新的实数:a2+b-1,例如把(3,-2)放入其中,就会得到:32+(-2)-1=6.现将实数对(-1,3)放入其中,得到实数m,再将实数对(m,1)放入其中后,得到的实数是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com