
题目列表(包括答案和解析)
12. (江西南昌一模)在平面直角坐标系中,正方形ABCD纸片如图放置,A(0,2),D(-1,0),抛物线
(江西南昌一模)在平面直角坐标系中,正方形ABCD纸片如图放置,A(0,2),D(-1,0),抛物线 经过点C.
经过点C.
(1)求点B、C的坐标;
(2)求抛物线的解析式;
(3)以直线AD为对称轴,将正方形ABCD纸片折叠,得到正方形ADEF,求出点E和点F坐标,并判断点E和点F是否在抛物线上,并说明理由.
答案:提示:(1)过B作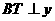 轴于T,过C作
轴于T,过C作 轴于P,可证得
轴于P,可证得
 .
.
 则
则
∴
∴B(-2,3).同理,
(2)抛物线 经过点C(-3,1),则得到
经过点C(-3,1),则得到
 ,解得
,解得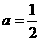 ,
,
所以抛物线解析式为 ;
;
 作
作 轴于Q,作
轴于Q,作 轴于P.
轴于P.
通过 ,得
,得
∴ ∴E(2,1).同理F(1,-1).
∴E(2,1).同理F(1,-1).
当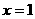 时,
时, ∴F(1,-1)在抛物线上.
∴F(1,-1)在抛物线上.
当 时,
时, ∴E(2,1)在抛物线上.
∴E(2,1)在抛物线上.
11.(济宁师专附中一模)
已知抛物线 经过(-1,0),(0,-3),(2,-3)三点.
经过(-1,0),(0,-3),(2,-3)三点.
⑴求这条抛物线的表达式;
⑵用配方法求这条抛物线的对称轴和顶点坐标.
答案:解:由已知,得 解得a=1,b=
解得a=1,b= -2,c=-3.
-2,c=-3.
所以y=x2-2x-3.
(2)对称轴x=1,顶点(1,-4) 配方略.
10.(2010广东省中考拟)如图10,在平面直角坐标系中,二次函数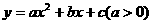 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO= .
.
(1)求这个二次函数的表达式.
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
(4)如图11,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.

答案:(1)方法一:由已知得:C(0,-3),A(-1,0)
将A、B、C三点的坐标代入得
解得:
所以这个二次函数的表达式为:
方法二:由已知得:C(0,-3),A(-1,0)
设该表达式为:
将C点的坐标代入得: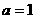
所以这个二次函数的表达式为:
(注:表达式的最终结果用三种形式中的任一种都不扣分)
(2)方法一:存在,F点的坐标为(2,-3)
理由:易得D(1,-4),所以直线CD的解析式为:
∴E点的坐标为(-3,0)
由A、C、E、F四点的坐标得:AE=CF=2,AE∥CF
∴以A、C、E、F为顶点的四边形为平行四边形
∴存在点F,坐标为(2,-3)
方法二:易得D(1,-4),所以直线CD的解析式为:
∴E点的坐标为(-3,0)
∵以A、C、E、F为顶点的四边形为平行四边形
∴F点的坐标为(2,-3)或(―2,―3)或(-4,3)
代入抛物线的表达式检验,只有(2,-3)符合
∴存在点F,坐标为(2,-3)
(3)如图,①当直线MN在x轴上方时,设圆的半径为R(R>0),则N(R+1,R),
代入抛物线的表达式,解得
②当直线MN在x轴下方时,设圆的半径为r(r>0),
则N(r+1,-r),
 代入抛物线的表达式,解得
代入抛物线的表达式,解得
∴圆的半径为 或
或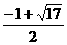 .
.
(4)过点P作y轴的平行线与AG交于点Q,
易得G(2,-3),直线AG为 .
.
设P(x, ),则Q(x,-x-1),PQ
),则Q(x,-x-1),PQ .
.

当 时,△APG的面积最大
时,△APG的面积最大
此时P点的坐标为 ,
, .
.
9. (2010 河南模拟)如图,曲线C是函数
(2010 河南模拟)如图,曲线C是函数 在第一现象内的图像,抛物线是函数
在第一现象内的图像,抛物线是函数 的图像,点
的图像,点 (n=1,2…)在曲线上,且x,y都是整数。
(n=1,2…)在曲线上,且x,y都是整数。
(1)求出所有的点 ;
;
(2)在 Pn中任取两点作直线,求所有不同直线的条数;
Pn中任取两点作直线,求所有不同直线的条数;
(3)从(2)中所有的直线中任取一直线,求所有直线与抛物线有公共的的概率。
答案:(1)∵x,y都是整数且 ,
,
∴x=1,2,3,6,
∴P1(1,6),(2,3),(3,2),(6,1);
(2)以P1 ,P2,,P3,P4中任取两点的直线有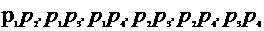 共六条;
共六条;
(3)∵只有直线 与抛物线有公共点,
与抛物线有公共点,
∴P= 。
。
8.(2010年厦门湖里模拟)一次函数y=x-3的图象与x轴,y轴分别交于点A,B.一个二次函数y=x2+bx+c的图象经过点A,B.
(1)求点A,B的坐标,并画出一次函数y=x-3的图象;
(2)求二次函数的解析式及它的最小值.
答案:解:(1)令 ,得
,得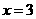 ,
, 点
点 的坐标是
的坐标是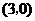
令 ,得
,得 ,
, 点
点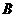 的坐标是
的坐标是
 图象如右所示。
图象如右所示。
(2) 二次函数
二次函数 的图象经过点
的图象经过点 ,
,
 ,解得:
,解得: .
.
 二次函数
二次函数 的解析式是
的解析式是 ,
,
 ,
,
 函数
函数 的最小值为
的最小值为 .
.
14. (2010福建模拟)如图,在平面直角坐标系中,直线
(2010福建模拟)如图,在平面直角坐标系中,直线 与
与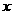 轴交于点A,与y轴交于点C. 抛物线
轴交于点A,与y轴交于点C. 抛物线 经过A、C两点,且与x轴交于另一点B(点B在点A右侧).
经过A、C两点,且与x轴交于另一点B(点B在点A右侧).
(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上一动点,过点M的直线EF平行y轴交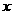 轴于点F,交抛物线于点E.求ME长的最大值;
轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线x轴下方是否存在点P,使以M、F、B、P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
解:(1) 当y=0时, 
 ∴A(-1, 0)
∴A(-1, 0)
当x=0时,
 ∴ C(0,-3)
∴ C(0,-3)
 ∴
∴ ∴
∴
 抛物线的解析式是:
抛物线的解析式是:
当y=0时,
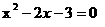 解得: x1=-1 x2=3 ∴ B(3, 0)
解得: x1=-1 x2=3 ∴ B(3, 0)
(2)由(1)知
B(3, 0) , C(0,-3) 直线BC的解析式是:
设M(x,x-3)(0≤x≤3),则E(x,x2-2x-3)
∴ME=(x-3)-( x2-2x-3)=- x2+3x =
∴当  时,ME的最大值=
时,ME的最大值=
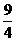
(3)答:不存在.
由(2)知 ME 取最大值时ME= 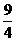 ,E
,E ,M
,M
∴MF= ,BF=OB-OF=
,BF=OB-OF= .
.
设在抛物线x轴下方存在点P,使以P、M、F、B为顶点的四边形是平行四边形,
则BP∥MF,BF∥PM. ∴P1  或 P2
或 P2 
 当P1
当P1  时,由(1)知
时,由(1)知
∴P1不在抛物线上.
 当P2
当P2  时,由(1)知
时,由(1)知
∴P1不在抛物线上.
综上所述:抛物线x轴下方不存在点P,使以P、M、F、B为顶点的四边形是平行四边形.
13.(2010天水模拟)如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴。
第(1)问:给出四个结论:①a>0;②b>0;③c>0;④a+b+c=0;.其中正确结论的序号(答对得3分,少选、错选均不得分)
 第(2)问:给出四个结论:①abc<0②2a+b>0③a+c=1④a>1.其中正确结论的序号(答对得5分,少选、错选均不得分)
第(2)问:给出四个结论:①abc<0②2a+b>0③a+c=1④a>1.其中正确结论的序号(答对得5分,少选、错选均不得分)
答案:a>0; b<0; C<0 abc>0;
abc>0;
2a+b>0 2a>-b 1>
 ①+②得 2a+2c=2 a+c=1 a=1-c
①+②得 2a+2c=2 a+c=1 a=1-c
12.(2010天水模拟)已知:抛物线y=-x2+4x-3与x轴相交于A、B,两点(A点在B点的左侧),顶点为这。
(1)求A、B、P三点坐标;
(2)在下面的直角坐标系内画出此抛物线的简图,并根据简图写出当x取何值时,函数值y大于零;
(3)确定此抛物线与直线y=-2x+6公共点的个数,并说明理由。
解:(1)-x2+4x-3=0 x2-4x+3=0 (x-1)(x-3)=0 x1=1,x2=3
H= =
= =2 k=
=2 k= =
=
∴A(1,0) B(3,0) P(2,1)
(2)略
(3)
将①代入②中 -x2+4x-3=-2x+6
-x2+6x-9=0
△=36-4×(-1)×(-9)
=36-36=0
∴只有一个
11.(2010年铁岭市加速度辅导学校)已知:抛物线 经过点
经过点 .
.
(1)求 的值;
的值;
 (2)若
(2)若 ,求这条抛物线的顶点坐标;
,求这条抛物线的顶点坐标;
(3)若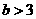 ,过点
,过点 作直线
作直线 轴,交
轴,交 轴于点
轴于点 ,交抛物线于另一点
,交抛物线于另一点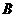 ,且
,且 ,求这条抛物线所对应的二次函数关系式.(提示:请画示意图思考)
,求这条抛物线所对应的二次函数关系式.(提示:请画示意图思考)
解:(1)依题意得: ,
,
 .
.
(2)当 时,
时, ,
,

 抛物线的顶点坐标是
抛物线的顶点坐标是 .
.
(3)当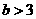 时,抛物线对称轴
时,抛物线对称轴 ,
,
 对称轴在点
对称轴在点 的左侧.
的左侧.
因为抛物线是轴对称图形, 且
且 .
.

 .
.
 .
.
又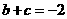 ,
, .
.
 抛物线所对应的二次函数关系式
抛物线所对应的二次函数关系式 .
.
解法2:(3)当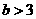 时,
时, ,
,
 对称轴在点
对称轴在点 的左侧.因为抛物线是轴对称图形,
的左侧.因为抛物线是轴对称图形,
 ,且
,且
 .
.
又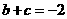 ,解得:
,解得:
 这条抛物线对应的二次函数关系式是
这条抛物线对应的二次函数关系式是 .
.
解法3:(3) ,
, ,
,
 分
分
 轴,
轴,
即: .
.
解得: ,即
,即
由 ,
, .
.

 这条抛物线对应的二次函数关系式
这条抛物线对应的二次函数关系式
10.(2010年江苏省泰州市济川实验初中中考模拟题) 某企业信息部进行市场调研发现:
信息一:如果单独投资A种产品,所获利润yA(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表:
|
x(万元) |
1 |
2 |
2.5 |
3 |
5 |
|
yA(万元) |
0.4 |
0.8 |
1 |
1.2 |
2 |
信息二:如果单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间存在二次函数关系:yB=ax2+bx,且投资2万元时获利润2.4万元,当投资4万元时,可获利润3.2万元.
(1)求出yB与x的函数关系式.
(2)从所学过的一次函数、二次函数、反比例函数中确定哪种函数能表示yA与x之间的关系,并求出yA与x的函数关系式.
(3)如果企业同时对A、B两种产品共投资15万元,请设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少?
答案:(1)yB=-0.2x2+1.6x,
(2)一次函数,yA=0.4x,
(3)设投资B产品x万元,投资A产品(15-x)万元,投资两种产品共获利W万元, 则W=(-0.2x2+1.6x)+0.4(15-x)=-0.2x2+1.2x+6=-0.2(x-3)2+7.8,
∴当x=3时,W最大值=7.8,
答:该企业投资A产品12万元,投资B产品3万元,可获得最大利润5.8 万元.
万元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com