
题目列表(包括答案和解析)
2.( 2010年山东菏泽全真模拟1)如图所示:边长分别为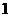 和
和 的两个正方形,其一边在同一水平线上,小正方形
的两个正方形,其一边在同一水平线上,小正方形 沿该水平线自左向右匀速穿过大正方形,设穿过的时间为
沿该水平线自左向右匀速穿过大正方形,设穿过的时间为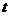 ,大正方形内除去小正方形部分的面积为
,大正方形内除去小正方形部分的面积为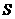 (阴影部分),那么
(阴影部分),那么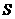 与
与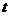 的大致图象应为( )
的大致图象应为( )
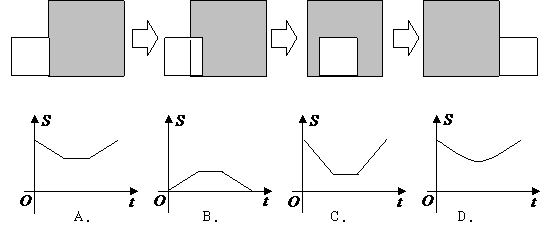
答案:A
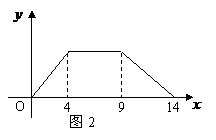
1.(2010年河南省南阳市中考模拟数学试题)如图1,在直角梯形ABCD中,∠B=90°,DC∥AB,动点P从B点出发,沿折线B→C→D→A运动,设点P运动的路程为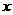 ,△ABP的面积为
,△ABP的面积为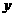 ,如果关于x的函数y的图像如图2所示,则△ABC的面积为( )
,如果关于x的函数y的图像如图2所示,则△ABC的面积为( )
 A.10 B.16 C.18 D.32
A.10 B.16 C.18 D.32

答:B
20.(2010年山东宁阳一模)用恰当的方法解方程:
答案:解:
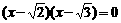

21 .(2010
.(2010 年山东宁阳一模)已知x1、x2是方程
年山东宁阳一模)已知x1、x2是方程 的两根,且
的两根,且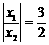 ,求m的值.
,求m的值.
答案:∵a=4,c=-6m2 ∴△≥0
则:x1x2≤0,又∵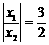 ,∴
,∴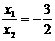
又∵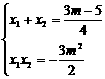 ,
,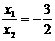 ,∴
,∴
∴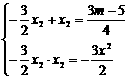 ,解得:m1=2,m2=5
,解得:m1=2,m2=5
19.( 2010年山东菏泽全真模拟1)用恰当的方法解方程 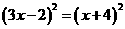
答案:解:解: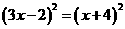
移项得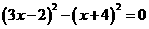
(3x-2+x+4)(3x-2-x-4)=0
(4x+2)(2x-6)=0
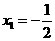 ,
,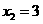
18.(2010年河南中考模拟题4)在四川省发生地震后,成都运往汶川灾区的物资须从西线或南线运输,西线的路程约800千米,南线的路程约80千米,走南线的车队在西线车队出发18小时后立刻启程,结果两车队同时到达.已知两车队的行驶速度相同,求车队走 南线所用的时间.
南线所用的时间.
答案:解:设车队走南线所用的时间为x小时,依题意得:
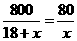
解这个方程得:x=2
经检验得x=2是方程的解。
答:车队走南线所用的时间为2小时。
17.(2010年江苏省泰州市济川实验初中中考模拟题) 已知:关于 的方程
的方程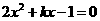
(1)求证:方程有两个不相等的实数根;(2)若方程的一个根是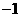 ,求
,求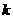 值及另一个根.
值及另一个根.
答案:(1) 证△=k2+8>0,
(2)k=1,x= .
.
16.(2010年吉林中考模拟题)孙明与李丽共同帮助校图书馆清点图书,李丽平均每分钟比孙明多清点10本.已知孙明清点完200本图书所用的时间与李丽清点完300本所用的时间相同,求孙明平均每分钟清点图书多少本.
答案:解:设孙明平均每分钟清点图书x本.
根据题意,得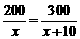 .
.
解这个方程,得 .
.
经检验,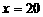 是原方程的解.
是原方程的解.
答:孙明平均每分钟清点图书20本.
15.(2010年福建模拟)某地为四川省汶川大地震灾区进行募捐,共收到粮食200吨,副食品120吨.现计划租用甲、乙两种货车共8辆将这批物资全部运往灾区,已知一辆甲种货车同时最多可装粮食40吨和副食品10吨,一辆乙种货车同时最多可装粮食和副食品各20吨.
(1) 将这些物资一次性运到目的地,有几种租用货车的方案?请你帮助设计出来.
(2) 若甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元,要使运输总费用最少?应选择哪种方案?
解:(1)设甲种货车有x辆 ,根据题意有:

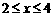 解之得:
解之得:
∴x的值是:2或3或4,有三种租用货车的方案。设计方案为:
① 租用甲种货车2辆,乙种货车6辆;
② 租用甲种货车3辆,乙种货车5辆;
③ 租用甲种货车4辆,乙种货车4辆.
(2)由(1)知:
方案① 的运输费用是:2×4000+6×3600=29600(元)
方案② 的运输费用是:3×4000+5×3600=30000(元)
方案③ 的运输费用是:4×4000+4×3600=30400(元)
∴应选用方案①:租用甲种货车2辆,乙种货车6辆,运输费用最少为29600元.
14.(2010年福建模拟)甲、乙两人从学校出发,前往距学校12千米的新华书店.甲每小时比乙多走2千米,乙比甲提前1小时出发,结果两人同时到达.求甲、乙两人每小时各走多少千米?
解:设甲每小时走x千米
,根据题意列方程得: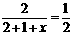
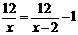
整理货单得:x2-2x-24=0
解这个方程方程得:x1=6 x2=-4
经检验x1
x2是原方程的解,但x2<0不符 合题意舍去,取x=6
合题意舍去,取x=6
∴x-2=4
答:甲每小时走6千米 ,乙每小时走4千米.
13.(2010年天水模拟)已知:关于x的两个方程x2+(m+1)x+m-5=0……①与mx2+(n-1)x+m-4=0……②方程①有两个不相等的负实数根,方程②有两个实数根。
(1)求证方程②的两根符号相同;
(2)设方程②的两根分别为α、β,若α:β=1:3,且n为整数,求m的最小整数值。
解:(1)x2+(m+1)x+m-5=0
△>0; △=(m+2)2-4(m-5)=m2+2m+1-4m+20>0
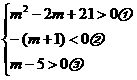
由②得m>-1 由③得 m>5
∴m>5
∴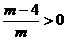 ∴方程②有两个同号实数根
∴方程②有两个同号实数根
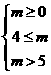 ∴m=6
∴m=6
∴m2-4m≥0 m(m-4)≥0
(2)α:β=1:3
4α=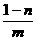 α=
α=
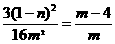
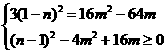
(n-1)2=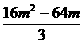 4m2-16m≥0
4m2-16m≥0
△2=(n-1)2-4m(m-4)
≥0 3α2=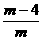
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com