2.不等式5x-4<6x的解集是________________.

答案：x＞-4

提示：解法与一元一次方程的解法类似.

1.若x<y<0,用“<”或“>”填空:

(1)-x________-y;(2)________;(3)|x|________|y|;

(4)x²________y²;(5)5x-1________5y-1;

(6)-3x________-3y.

答案：＞　 ＞　 ＞　 ＞　 ＜　 ＞

提示：利用不等式的性质.

11.如图7-24,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点.

图7-24

(1)当点P移动到AB、CD之间时,如图7-24(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论.

(2)当点P移动到AB的外侧时,如图7-24(2),是否仍有(1)的结论?如果不是________________,请写出你的猜想(不要求证明).

(3)当点P移动到如图7-24(3)的位置时,∠P与∠A、∠C又有怎样的关系?能否利用(1)的结论来证明?还有其他的方法吗?请写出一种.

证明：(1)∠P=∠A+∠C,

延长AP交CD与点E.

∵AB∥CD,∴∠A=∠AEC.

又∵∠APC是△PCE的外角,

∴∠APC=∠C+∠AEC.

∴∠APC=∠A+∠C.

(2)否；∠P=∠A-∠C.

(3)∠P=360°-(∠A+∠C).

①延长BA到E，延长DC到F,

由(1)得∠P=∠PAE+∠PCF.

∵∠PAE=180°-∠PAB，∠PCF=180°-∠PCD,

∴∠P=360°-(∠PAB+∠PCD).

②连结AC.

∵AB∥CD,∴∠CAB+∠ACD=180°.

∵∠PAC+∠PCA=180°-∠P,

∵∠CAB+∠ACD+∠PAC+∠PCA=360°-∠P,

即∠P=360°-(∠PAB+∠PCD).

(本题答案不唯一)

10.如图7-23,玻璃厂工人为了测试一块玻璃的两个面是否平行,采用了这样一个小办法:一束光线从空气射入玻璃中会发生折射现象,光线从玻璃射入空气也会发生折射现象,如图所示,如果l∥m,∠1=∠2,那么工人就会判定玻璃的两个面平行.你明白这个办法的道理吗?请给出证明.

图7-23

提示：反向延长l、m,利用“对顶角相等”和“两直线平行，内错角相等”来说明.

9.如图7-22,已知PA平分∠CAB,PC平分∠ACD,AB∥CD.求证:AP⊥PC.

图7-22

证明：∵PA平分∠CAB，PC平分∠ACD,

∴∠PAC=∠CAB，∠PCA=∠ACD,

∴∠PAC+∠PCA=∠CAB+∠ACD=(∠CAB+∠ACD).

∵AB∥CD,

∴∠CAB+∠ACD=180°.

∴∠PAC+∠PCA=90°.

∵△ACP中，∠PAC+∠PCA+∠P=180°,

∴∠P=90°,∴AP⊥PC.

8.如图7-21,已知∠1+∠2=180°,求证:∠3=∠4.

图7-21

证明：把∠2的对顶角注为∠5.

∵∠2=∠5(对顶角相等),∠1+∠2=180°(已知),

∴∠5+∠1=180°(等量代换).

∴a∥b(同旁内角互补，两直线平行).

∴∠3=∠4(两直线平行，同位角相等).

7.小明、小亮、小刚、小颖一起研究一道数学题.如图7-20,已知EF⊥AB,CD⊥AB,

小明说:“如果还知道∠CDG=∠BFE,则能得到∠AGD=∠ACB.”

小亮说:“把小明的已知和结论倒过来,即由∠AGD=∠ACB,

可得到∠CDG=∠BFE.”

小刚说:“∠AGD一定大于∠BFE.”

小颖说:“如果连结GF,则GF一定平行于AB.”

他们四人中,有_________________个人的说法是正确的.

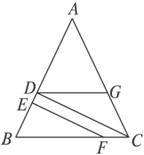
图7-20

A.1　　　　　　　　 B.2　　　　　　　　 C.3　　　　　　　　　 D.4

答案：C

提示：平行线的性质与判定.

6.如图7-19,下列条件中,不能判断AD∥BC的是

图7-19

A.∠1=∠3　　　　　　　　　　　　　　　 B.∠2=∠4

C.∠EAD=∠B　　　　　　　　　　　　　　 D.∠D=∠DCF

答案：B

提示：平行线的判定.

5.(2010山东烟台中考)如图7-18,已知AB∥CD,∠1=30°,∠2=90°,则∠3等于

A.60°　　　　　　　 B.50°　　　　　　　 C.40°　　　　　　　 D.30°

图7-18

答案：A

提示：过∠2顶点作AB的平行线,由两直线平行内错角相等.

4.如图7-17,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.

对于本题小丽是这样证明的,请你将她的证明过程补充完整.

图7-17

证明:∵∠BAP与∠APD互补,(已知)

∴AB∥CD.(　　　　　　　 )

∴∠BAP=∠APC.(　　　　　　　 )

∵∠BAE=∠CPF,(已知)

∴∠BAP-∠BAE=∠APC-∠CPF,

( 　　　　　　)

即_________________=__________________.

∴AE∥FP.

∴∠E=∠F.

答案：同旁内角互补，两直线平行　 两直线平行，内错角相等(平行线的性质)　 等式性质　 ∠EAP　 ∠APF　 (等角减去等角得等角)