1. 五张标有1、2、3、4、5的卡片，除数字外，其他没有任何区别.现将它们背面朝上，从中任取一张，得到卡片的数字为偶数的概率是________________.

答案：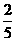

提示：摸到5种卡片的可能结果是5种，摸到偶数的可能性是2种.

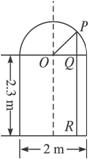
17.一辆装满货物的卡车,高2.5米,宽1.6米,要开进厂门形状如图8-46所示的某工厂,问这辆卡车能否通过厂门(厂门上方为半圆形拱门)?说明你的理由.

图8-46

提示：如图，作厂门的对称轴，求出PR的长，只要PR＞车高2.5，就说明卡车能通过厂门.

在Rt△OPQ中，由勾股定理得PQ==0.6米,

∴PR=0.6+2.3=2.9＞2.5.

∴这辆卡车能通过厂门.

16.已知:a、b、c为△ABC的三边,且满足a²c²-b²c²=a⁴-b⁴,试判断△ABC的形状.

解:∵a²c²-b²c²=a⁴-b⁴,①

∴c²(a²-b²)=(a²+b²)(a²-b²).②

∴c²=a²+b².③

∴△ABC是直角三角形.

问:

(1)在上述解题过程中,从哪一步开始出现错误?请写出该步的代号: ______________;

(2)错误的原因为_________________________________________________________________;

(3)本题正确的解题过程:

答案：(1)③　 (2)除式可能为零

(3)∵a²c²-b²c²=a⁴-b⁴,

∴c²(a²-b²)=(a²+b²)(a²-b²).

∴a²-b²=0或c²=a²+b².

当a²-b²=0时，a=b；

当c²=a²+b²时，∠C=90度,

∴△ABC是等腰三角形或直角三角形.

提示：(1)(2)两边都除以a²-b²,而a²-b²的值可能为零，由等式的基本性质，等式两边都乘以或除以同一个不为0的整式，等式仍然成立.

(3)根据等式的基本性质和勾股定理，分情况加以讨论.

15.甲、乙两船上午11时同时从港口A出发,甲船以每小时20海里的速度向东北方向航行,乙船以每小时15海里的速度向东南方向航行,求下午1时两船之间的距离.

图8-45

答案：50海里.

提示：东北方向航行，东南方向航行，则夹角为90度，根据勾股定理，相距= =50.

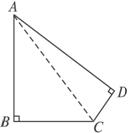
14.有一块土地形状如图8-44所示,∠B=∠D=90°,AB=20米,BC=15米,CD=7米,请计算这块地的面积.

图8-44

答案：234米².

提示：连结AC，将四边形分割成两个三角形，其面积为两个三角形的面积之和，根据勾股定理求出AC，进而求出AD.AC==25,AD=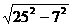=24，面积为AB×BC+AD×CD=234米².

13.如图8-43，在四边形ABCD中,AB=12 cm,BC=3 cm,CD=4 cm,∠C=90°.

图8-43

(1)求BD的长;

(2)当AD为多少时,∠ABD=90°?

(1)答案：5.

提示：在△BDC中，∠C=90°，BC=3 cm，CD=4 cm，根据勾股定理，BD²=BC²+CD²，求得BD=5 cm.

(2)答案：13.

提示：根据勾股定理的逆定理，三角形两边的平方和等于斜边的平方，则三角形是直角三角形，所以AD=13时，可满足AD²=BD²+AB²，可说明∠ABD=90°，AD==13.

12.一职工下班后以50米/分的速度骑自行车沿着东西马路向东走了5.6分,又沿南北马路向南走了19.2分到家,则他的家离公司距离为______________米.

A.100　　　　　　　 B.500　　　　　　　 C.1 240　　　　　　　 D.1 000

答案：D

提示：由于东西方向与南北方向互相垂直，两段路程与家离公司距离形成直角三角形，根据勾股定理求得家离公司距离==1 000米.

11.一个圆桶底面直径为24 cm,高32 cm,则桶内所能容下的最长木棒为

A.20 cm　　　　　　 B.50 cm　　　　　　 C.40 cm　　　　　　　 D.45 cm

答案：C

提示：根据勾股定理，最长木棒长的平方=24²+32²，解得40 cm.

10.下列说法不正确的是

A.三个角的度数之比为1∶3∶4的三角形是直角三角形

B.三个角的度数之比为3∶4∶5的三角形是直角三角形

C.三边长度之比为3∶4∶5的三角形是直角三角形

D.三边长度之比为5∶12∶13的三角形是直角三角形

答案：B

提示：三个角的度数之比中有两个之和等于另一个，可以判定是直角三角形，另外两边的平方和=第三边的平方，也可以判定是直角三角形，三个角的度数之比为3∶4∶5的三角形，三个角分别是45度、60度和75度，不是直角三角形.

9.下列是勾股数的一组是

A.4,5,6　　　　　　　 B.5,7,12　　　　　　 C.12,13,15　　　　　　 D.21,28,35

答案：D

提示：满足a²+b²=c²的正整数是勾股数，只有21²+28²=35²，所以选D.