
题目列表(包括答案和解析)
1.反比例函数y=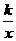 过点(2,3),则k=_____________________;反比例函数y=
过点(2,3),则k=_____________________;反比例函数y= 过点(-2,3),则k=_________________.
过点(-2,3),则k=_________________.
答案:6 -5
提示:点在函数图象上,则点的坐标满足函数关系式,把点的坐标值代入解析式求k的值.3= ,k=6;
,k=6; =3,k-1=-6,k=-5.
=3,k-1=-6,k=-5.
16.(1)甲、乙两人同时从A地出发去B地,甲的速度是乙的1.5倍.已知A、B两地相距27千米,甲到达乙地3小时后,乙才到达,求甲、乙两人的速度.
(2)甲、乙两人同时从相距9千米的A、B两地同时出发,若相向而行,则1小时相遇,若同向而行,乙在甲前面,则甲走了18千米后追上乙,求甲、乙两人的速度.
(1)答案:甲为4.5千米/时,乙为3千米/时.
提示:根据甲比乙少用3小时为等量关系列出方程.设乙的速度为x千米/时,列方程得 -
- =3,甲为4.5千米/时,乙为3千米/时.
=3,甲为4.5千米/时,乙为3千米/时.
(2)答案:甲为6千米/时,乙为3千米/时.
提示:设甲的速度为x千米/时,相向而行,1小时相遇,则(甲速+乙速)×1=9,所以乙速=9-x.又若同向而行,乙在甲前面,则甲走了18千米后追上乙,即甲走18千米所用时间=乙走9千米所用的时间相等,由此可列出方程,得 =
= ,甲为6千米/时,乙为3千米/时.
,甲为6千米/时,乙为3千米/时.
15.设轮船在静水中的速度为v,该船在流水(水流速度为u)中从A顺流到B,再从B逆流返回到A所用的时间为T;假设当河流为静水时,该船从A到B再返回A,所用时间为t,A、B两地之间的距离为s.
(1)用代数式表示时间T.
(2)用代数式表示时间t.
(3)你能确定T与t之间的大小关系吗?说明理由.
(1)答案:T=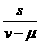 +
+ .
.
提示:由航行时间= ,顺水速度是v+μ,顺水时间为
,顺水速度是v+μ,顺水时间为 ,逆水速度是v-μ,逆水时间为
,逆水速度是v-μ,逆水时间为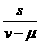 ,总时间为T=
,总时间为T=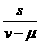 +
+ .
.
(2)答案:t= .
.
提示:由航行时间= ,路程为2s,速度为v,时间为t=
,路程为2s,速度为v,时间为t= .
.
(3)答案:T>t.
提示:T=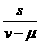 +
+ =
= =
= ,t=
,t= =
= ,分子相同,只要比较分母即可,分母越小,分式的值越大,v2-μ2<v2,所以T>t.
,分子相同,只要比较分母即可,分母越小,分式的值越大,v2-μ2<v2,所以T>t.
14.当A、B、C取何值时,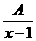 +
+ +
+ =
= .
.
答案:A=3,B=-2,C=-1.
提示:由恒等式的性质知,通分加减后,左右两边分母相同,则分子也相同,所以分子的各项系数也相同.
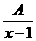 +
+ +
+ =
=
=
= ,
,
则A+B+C=0,-A-3B=3,-2A+2B-C=-9,解得A=3,B=-2,C=-1.
13.解下列分式方程:
(1) +
+ =0;
=0;
(2) -
- =
= .
.
(1)答案:a=-2.5.
提示:解分式方程的一般步骤是:去分母,化成整式方程,解整式方程;检验是否是增根;得到原方程的解.去分母乘以(a+1)(2-a),得到2-a+3(a+1)=0,解得a=-2.5,检验,将a=-2.5代入(a+1)(2-a)≠0,所以原方程的解是a=-2.5.
(2)答案:x=-2.
提示:先求各分母的最小公倍数,去分母乘以x2-4,得(x-2)2-16=(x+2)2,所以x2-4x+4-16=x2+4x+4,解得x=-2,检验,将x=-2代入x2-4=0,所以x=-2是增根,原方程无解.
12.计算与化简:
(1)(xy-x2)÷ ;
;
(2) -a-1.
-a-1.
(3)先化简,后求值:( +
+ )÷
)÷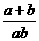 ,其中a=25,b=
,其中a=25,b=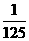 .
.
(1)答案:-x2y.
提示:根据分式的除法法则,把分式的分子和分母颠倒位置后与被除式相乘,-x(x-y)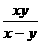 =-x2y.
=-x2y.
(2)答案: .
.
提示:把-a-1看成一个整体,分母是1,然后再通分化成同分母分式相加减. -
- =
=  =
= .
.
(3)答案: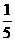 .
.
提示:变成乘法后可利用乘法分配律,运用运算律可以使计算简便,也可以先算括号内的,再进行分式的除法.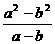 ×
× =ab.
=ab.
11.小明通常上学时走上坡路,途中平均速度为m千米/时,放学回家时沿原路返回,通常平均速度为n千米/时,则小明上学和放学路上的平均速度为______________千米/时.
A.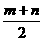 B.
B. C.
C. D.
D.
答案:C
提示:由平均速度=总路程/总时间,可设路程为s,上坡时间为 ,返回时间为
,返回时间为 ,总时间为
,总时间为 +
+ =
= ,平均速度为2s÷
,平均速度为2s÷ =
= .
.
10.全民健身活动中,组委会组织了长跑队和自行车队进行宣传,全程共10千米,自行车队的速度是长跑队速度的2.5倍,自行车队出发半小时后,长跑队才出发,结果长跑队比自行车队晚到了2小时,如果设长跑队跑步的速度为x千米/时,那么根据题意可列方程为
A. +2=
+2= +
+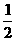 B.
B. -
- =2-0.5
=2-0.5
C. -
- =2-0.5
D.
=2-0.5
D. -
- =2+0.5
=2+0.5
答案:C
提示:自行车队的速度是长跑队的速度的2.5倍,可得自行车队的速度为2.5x,整个过程长跑队一共比自行车队多用了2-0.5小时,据此可列方程 -
- =2-0.5.
=2-0.5.
9.沿河的上游和下游各有一个港口A、B,货船在静水中的速度为a千米/时,水流的速度为b千米/时,那么一艘货船从A港口出发,在两港之间不停顿地往返一次所需的时间是
A.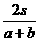 小时
B.
小时
B. 小时
小时
C.( +
+ )小时
D.(
)小时
D.(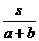 +
+ )小时
)小时
答案:D
提示:依据顺水速度=静水速度+水流速度,逆水速度=静水速度-水流速度,则顺水速度为a+b,时间为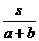 ,逆水速度为a-b,时间为
,逆水速度为a-b,时间为 ,所以往返时间为
,所以往返时间为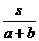 +
+ .
.
8.下列分式中,不论x取何值,都有意义的是
A. B.
B.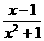
C. D.
D.
答案:B
提示:不论x取何值,都有意义,就是说不论x取何值,分式的分母都不等于0,而x2+1永远不等于0,选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com