4.若a、b互为倒数,c、d互为相反数,则+c+d=__________________.

答案：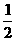

提示：ab=1，c+d=0.

3.早春二月的某一天,A市的平均气温为-5℃,B市的平均气温为3℃,则当天B比A市的平均气温高____________℃.

答案：8

提示：3-(-5)=8.

2.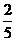的倒数与它的相反数的商是___________________.

答案：-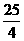

提示：÷(-)=-.

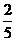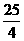1.-5的相反数是___________________.-3的绝对值是__________________,的算术平方根是__________________.

答案：5　 3　 0.5

提示：由相反数、绝对值、平方根的定义可得.

17.实践探究

如图9-18，某工地工人为了用起重机吊起两根半径为10厘米和30厘米的钢管，需要先用钢丝绳把两根钢管扎紧，问扎紧这两根钢管的钢丝绳至少要多长？(打节部分不计，精确到0.1厘米)

图9-18

提示：由题意知圆外的两条钢丝与两圆外切,由切点与圆心构造一个直角梯形,再化为直角三角形.

利用勾股定理、三角函数及弧长公式求得,

即2×++

=40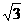+40π+π

≈247.2.

16.(2010江苏盐城中考)已知AB为⊙O的直径，P为AB弧的中点.

(1)若⊙O′与⊙O外切于点P(见图9-17甲)，AP，BP的延长线分别交⊙O′于点C、D，连结CD，则△PCD是_____________三角形；

(2)⊙O′与⊙O相交于点P，Q(见图9-17乙)，连结AQ、BQ并延长分别交⊙O′于点E、F，请选择下列两个问题中的一个作答：

　 问题一：判断△PEF的形状，并证明你的结论；

　 问题二：判断线段AE与BF的关系，并证明你的结论.

　 我选择问题_____________________________，结论：_______________________________.

　 证明：

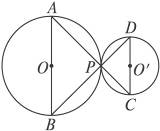
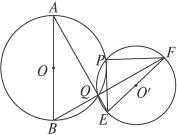
甲　　　　　　　　　　　　　 乙

图9-17

解：(1)等腰直角.

甲

(2)问题一：△PEF是等腰直角三角形.

证明：连结PA、PB.

∵AB是直径,

∴∠AQB=∠EQF=90°.

∴EF是⊙O′的直径.∴∠EPF=90°.

在△APE和△BPF中,

∵PA=PB,∠PBF=∠PAE,

∠APE=∠BPF=90°+∠EPB,

∴△APE≌△BPF.

∴PE=PF.∴△PEF是等腰直角三角形.

问题二：连结PA、PB.

由(1)可证△APE≌△BPF,∴AE=BF.

乙

提示：直径所对的圆周角是直角,并通过对顶角将两个圆中的相关量联系起来.

答案：247.2厘米

15.如图9-16，已知两同心圆，大圆的弦AB切小圆于M，若环形的面积为9π，求AB的长.

图9-16

提示：大圆的半径为R,小圆的半径为r,连结OA,OM,

由题意得πR²-πr²=9π,即R²-r²=9,因为AB切小圆于M,所以OM⊥AB.

由垂径定理得AM=BM,AM²=OA²-OM²=R²-r²=9,

所以AM=3.所以AB=6.

14.在半径为5厘米的圆中有一个内接等腰三角形，等腰三角形的底边长为8厘米，求等腰三角形的周长.

答案：8+8(或8+4)厘米.

提示：由圆心向底边作垂线,由勾股定理可得弦心距为3,有两解,从而等腰三角形底边上的高分别为2和8,再由勾股定理可得腰长为2和4,所以周长为(8+4)和(8+8)厘米.

13.如图9-15，一个残破的圆轮，为了再制作一个同样大小的圆轮，请用圆规、直尺作出它的圆心和半径.

图9-15

提示：在圆弧上任意取3个点A,B,C,分别作AB,AC的垂直平分线,交点就是圆心.

12.粮仓的顶部是一个圆锥形，其底面周长为32米，母线长为7米，为防雨需在粮仓顶部铺上油毡，需用________________平方米的油毡.(不计接头)

答案：112

提示：由周长可计算出半径,然后再利用圆锥侧面积公式计算出结果.