
题目列表(包括答案和解析)
下面每小题给出的四个选项中,只有一个是正确的。注意可以用多种不同的方法来选取正确答案。
1.[原创]按100分制60分及格来算,满分是150分的及格分是( )
A、60分 B、72分 C、90分 D、105分
24.(本小题满分12分)
已知:在平面直角坐标系中,抛物线 (
( )交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
⑴求该抛物线的解析式及顶点D的坐标;
⑵若点P(0,t)是y轴上的一个动点,请进行如下探究:
探究一:如图1,设△PAD的面积为S,令W=t·S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.
(参考资料:抛物线 对称轴是直线x=
对称轴是直线x= )
)


图1 图2
23.(本小题满分10分)
甲喜欢喝西湖龙井茶,乙喜欢喝咖啡。1包西湖龙井茶叶,甲、乙两人一起喝10天喝完,甲单独喝则比乙单独喝快48天喝完; 1罐咖啡,甲、乙两人一起喝12天喝完,乙单独喝则需20天喝完.
(1)甲、乙单独喝完1包茶叶各需多少天?
(2)假如现在让甲单独先喝咖啡,而让乙单独先喝茶,甲在有咖啡的情况下决不能喝自己喜欢的茶,而乙在有茶叶的情况下决不能喝自己喜欢的咖啡,问两人一起喝完1包茶叶和1罐咖啡需要多少天?
22.(本小题满分10分)
已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE、BD.
(1)求证:△AGE≌△DAB
(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.

21.(本小题满分8分)
为了了解某校初三年级1000名学生的视力情况,随机抽查了部分初三学生的视力情况,经过统计绘制了频率分布表和频率分布直方图.
频率分布表 频率分布直方图
|
分组 |
频数 |
频率 |
|
3.95-4.25 |
6 |
0.12 |
|
4.25-4.55 |
 |
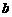 |
|
4.55-4.85 |
17 |
0.34 |
|
4.85-5.15 |
15 |
0.3 |
|
5.15-5.45 |
4 |
0.08 |
|
合计 |
50 |
1 |
 根据图表中的信息回答下列问题:
根据图表中的信息回答下列问题:
(1)写出频率分布表中的 ,
, ,补全频率分布直方图;
,补全频率分布直方图;
(2)判断这组数据的中位数落在哪个小组内?
(3)若视力在4.85-5.15范围内均属于正常,不需要矫正.试估计该校初三学生视力正常的人数约为多少人?
20.(本小题满分8分)
如图,已知线段 .
.
 (1)只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC,使AB=
(1)只用直尺(没有刻度的尺)和圆规,求作一个直角三角形ABC,使AB= ,BC=
,BC= ,∠ABC=Rt∠(要求保留作图痕迹,不必写出作法);
,∠ABC=Rt∠(要求保留作图痕迹,不必写出作法);
(2)若在(1)作出的RtΔABC中,AB=4cm,求AC边上的中线长 .
19.(本小题满分6分)
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角 处沿着木柜表面爬到柜角
处沿着木柜表面爬到柜角 处.
处.
(1)请你在备用图中画出蚂蚁能够最快到达目的地的可能路径;
 (2)当
(2)当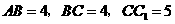 时,求蚂蚁爬过的最短路径的长.
时,求蚂蚁爬过的最短路径的长.
18.(本小题满分6分)
 如图,从一个直径是2的圆形铁皮中剪下一个圆心角为
如图,从一个直径是2的圆形铁皮中剪下一个圆心角为 的扇形.
的扇形.
(1)求这个扇形的面积(结果保留 );
);
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆
作为底面与此扇形围成一个圆锥?请说明理由.
解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.
17.(本小题满分6分)
 如图,在3×3的方阵图中,填写了一些数和代数式(其中每个代数式都表示一个数),使得每行的3个数、每列的3个数、斜对角的3个数之和均相等.
如图,在3×3的方阵图中,填写了一些数和代数式(其中每个代数式都表示一个数),使得每行的3个数、每列的3个数、斜对角的3个数之和均相等.
(1)求x,y的值;
(2)在备用图中完成此方阵图.
16. 如图,图1是一块边长为1,面积记为S1的正三角形纸板,沿图1的底边剪去一块边长
为 的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的
的正三角形纸板后得到图2,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的 )后,得图3,4,…,记第n(n≥3) 块纸板的面积为Sn,则Sn-1-Sn =
.
)后,得图3,4,…,记第n(n≥3) 块纸板的面积为Sn,则Sn-1-Sn =
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com