1、在比例尺为1:5000的地图上，量得甲、乙两地的距离为25cm，则甲、乙两点的实际距离是(　 )

A .1250km　　 B .125km　　　 C. 12.5km　　　 D .1.25km

(1)、　　　　　　　　　　　　　 的两个三角形相似；

(2)　　　　　　　　　　　　 的两个三角形相似；

(3) 　　　　　　　　　　　　　　的两个三角形相似。

(4) 平行于三角形一边的直线和其他两边相交，所构成的三角形和原三角形　　　　　　 。

[例题解析]

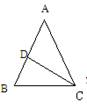
例1、如图，在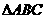中D是AB边上一点，连接CD，要使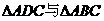相似，应添加的条件是　　　　　　 。

解析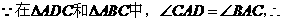：根据三角形相似的判定定理，只要，满足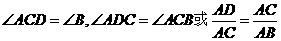三个条件中的一个即可。

反思：此题是一道条件开放题，答案不唯一，需同学们找出一个即可，此题为近年中考热点。

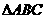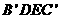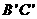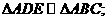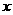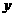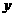例2、如图，已知，中，=，AB=6，AC=8，D是AB上一动点，DEBC,交AC于点E，将四边形BDEC沿DE向上翻折，得四边形,与AB、AC分别交于点M、N。(1)证明：(2)设AD为，梯形MDEN的面积为，试求与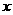的函数关系式。当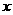为何值时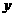有最大值？　　　

　 　解析：第(1)问，由DE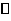BC得.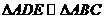

第(2)问，先用三角形面积之比等于相似比的平方，算出

再利用。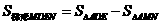

　　 反思：由相似图形的相似比建立函数模型是中考偏难题型常用思路，同学们需抓住相似比与边长比、面积比、中线比等之间的关系列出相应的函数关系式，建立数学模型来解题。

(1)、对应角　　　　　 ，对应边　　　　 。

(2)、周长之比等于　　　　　　 ，面积之比等于　　　　　 。

(3)、相似三角形对比高的比、对应角平分线的比和对应中线的比等于　　　　 。相似三角形的定义：如果两个三角形的对应角　　　　　 ，对应边　　　　 ，那么这两个三角形叫做相似三角形。

(1)、定理：三条平行线截两条直线，所得的对应线段　　　　　 。

(2)、推论：平行于三角形一边的直线截其他两边(或两边的延长线)，所得的对应线段　　　　　　 。

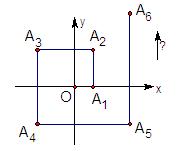
21、如图，一个机器人从O点出发，向正东方向走3m,到达A₁点，再向正北走6m到达A₂点，再向正西走9m到达点，再向正南走12m，到达点，再向正东方向走15m到达A₅点，按如此规律走下去，当机器人走到A₆点时，A₆点的坐标是 ________，你能找出其中的规律吗？并试求出A₁₀₀的坐标是多少？

20、如图，我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长为1)，根据象棋中“马”走“日”的规定，若“马”的位置在图中的点P．

(1)写出下一步“马”可能到达的点的坐标_________；

(2)顺次连接(1)中的所有点，得到的图形是_________图形(填“中心对称”，“旋转对称”，“轴对称”)；

(3)指出(1)中关于点P成中心对称的点_________．

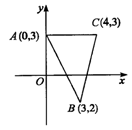
19、试判断以A(-1，-1)，B(5，-1)，C(2，2)为顶点的三角形的形状，并求出它的面积。

18、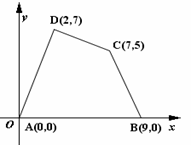 在如图所示的直角坐标系中，四边形ABCD各顶点的坐标分别为A(0,0)、B(9，0)、C(7，5)、D(2，7)，试求四边形ABCD的面积。

17、如图，利用关于原点对称的点的坐标的特点，作出△ABC关于原点对称的图形．

16、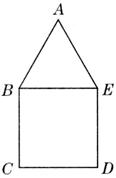如图，四边形BCDE是一个边长为2的正方形，△ABC是等边三角形。建立适当的坐标系，写出A，B，C，D，E各点的坐标。