
题目列表(包括答案和解析)
24.(本题12分)如图所示,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且满足6a-3b=2.
(1)求抛物线的解析式.
(2)如果点P由点A出发沿AB边以2cm/s的速度向点B运动,同时点Q由点B出发沿BC边以1cm/s的速度向点C运动,当其中一点到达终点时,另一点也随之停止运动. 设S=PQ2(cm2)
 ①试求出S与运动时间t之间的函数关系式,并写出t的取值范围
①试求出S与运动时间t之间的函数关系式,并写出t的取值范围
②当S= 时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形? 如果存在,求出R点的坐标;如果不存在,请说明理由.
时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形? 如果存在,求出R点的坐标;如果不存在,请说明理由.
23.(本题10分)某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价
为8元/千克,下面是他们在活动结束后的对话。
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可获取利润750元.
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系.
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)当销售单价为何值时,该超市销售这种水果每天获取的利润达到600元?[利润=销售量×(销售单价-进价)]
(3)一段时间后,发现这种水果每天的销售量均不低于225千克.则此时该超市销售这种水果每天获取的最大利润是多少?

22. (本题10分)如图,已知Rt△
(本题10分)如图,已知Rt△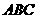 ,
, ,
, 的平分线
的平分线 交
交 于点
于点 ,
, 的垂直平分线分别交
的垂直平分线分别交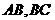 于点
于点 ,
,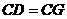 .
.
(1)请以图中的点为顶点(不增加其他的点)分别构造两个菱形和两个等腰梯形.那么,构成菱形的四个顶点是 ▲ 或 ▲ ;构成等腰梯形的四个顶点是 ▲ 或 ▲ ;
 (2)请你各选择其中一个图形加以证明。
(2)请你各选择其中一个图形加以证明。
(2)请把频数分布直方图补充完整;
(3)如果一分钟跳绳次数不低于120次的同学视为达标,八年级同学一分钟跳绳的达标率不低于90%,那么八年级同学至少有多少人?

21. (本题8分)如图,已知AB是⊙O的直径,直线CD与
(本题8分)如图,已知AB是⊙O的直径,直线CD与
⊙O相切于点C,过A作AD⊥CD,D为垂足。
(1)求证:AC平分∠DAB。
(2)若AD=3,AC= ,求AB的长。
,求AB的长。
(第21题图)
20.(本题8分)我市某校积极开展阳光体育活动,师生每天锻炼1小时,老师对本校八年级段学生进行一分钟跳绳测试,并对跳绳次数进行统计,绘制了八(1)班一分钟跳绳次数的频数分布直方图和八年级其余班级一分钟跳绳次数的扇形统计图。已知在图1中,组中值为150次一组的频率为0.2。(说明:组中值为190次的组别为180≤次数<200) 请结合统计图完成下列问题:
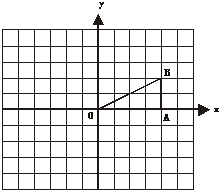
19.(本题6分)如右图,在Rt△OAB中,
∠OAB=90°,且点 的坐标为(4,2),将△OAB
的坐标为(4,2),将△OAB
绕点O逆时针旋转90°后得△OA1B1。
(1)在图中作出△OA1B1并直接写出A1,B1的坐标;
(2)求点B旋转到点B1所经过的路线长(结果保留π).
|
18. (本题6分)解不等式组
(本题6分)解不等式组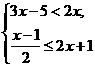 并将其解集在数轴上表示出来.
并将其解集在数轴上表示出来.
17.(本题6分)先化简,再求值: ,其中
,其中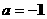
16. 如图,Rt△ABC中,∠C= Rt∠,AC=10,BC=20,
如图,Rt△ABC中,∠C= Rt∠,AC=10,BC=20,
正方形DEFG顶点G、F分别在AC、BC边上,D、
E在边AB上,且JE//GH//BC,IF//DK//AC,则四边
形HIJK 的面积= 。
|
14.圆锥的底面半径为1,侧面积为4π,则圆锥的高线长
为 ▲ 。
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com