
题目列表(包括答案和解析)
3.已知 ,则
,则 等于
等于
A.-6 B.6 C.-1 D.1
2.全球可被人类利用的淡水总量仅占地球上总水量的0.00003,因此珍惜水、保护水,是我们每一位公民义不容辞的责任.其中数字0 .00003用科学记数法表示为
.00003用科学记数法表示为
A. B.
B.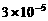 C.
C. D.
D.
1.6的倒数是
A. -6 B.±
-6 B.± C.
C.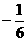 D.
D.
26.(12分)如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)求证:△ODM∽△MCN;
(2)设DM = x,OA=R,求R关于x 的函数关系式;
 (3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.
25.(10分)坐落在伊丽莎白港的曼德拉海湾球场是2010年南非世界杯的比赛场地之一,这座球场就是以南非黑人领袖纳尔逊-曼德拉来命名的。某公司承担该球场草坪的铺设和养护任务,计划用A 、B两种草皮共5000块,其中比赛期间的养护费用按一次性计算,赛事组委会要求A 、B两种草皮的铺设块数必须是100的倍数,该公司所筹铺设资金不少于23500美元,但不超过24000美元,此两种类型草皮的成本和养护费如下表:
|
类 型 |
A |
B |
|
成本(美元/块) |
5 |
4 |
|
养护费(美元/块) |
0.2 |
0.15 |
(1)请你为该公司设计铺设的可行性方案?
(2)你认为该公司如何进行铺设所花费用最少?
(3)根据市场调查,B型草皮的成本不会改变,A型草皮的成本将会下降m元(m>0),该公司应该如何进行铺设所花费用最少?(注:费用=成本+养护费)
24.(7分)已知二次函数 的图象过点A(-3,0)和点B(1,0),且与
的图象过点A(-3,0)和点B(1,0),且与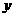 轴交于点C,D点在抛物线上且横坐标是 -2.
轴交于点C,D点在抛物线上且横坐标是 -2.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值.

23.(8分)已知:在△ABC中,AD为中线,如图1,将△ADC沿直线AD翻折后点C落
在点E处,连结BE和CE.
(1)求证:BE⊥CE;(3分)
(2)若AC=DC(如图2),请在图2中画出符合题意的示意图,并判断四边形ADBE是
什么四边形?请证明你的结论。(5分)


21.(9分)已知,如图是一个等腰直角三角形和一个正三角形.请你设计两种不同的分法,将它们分别分割成3个三角形,使得等腰直角三角形中的3个小三角形和正三角形中的3个小三角形分别相似.请画出三角形的分割线段,标出所得小三角形的各个内角的度数.(画图工具不限,不要求写画法,不要求说明理由).

 分法一:
分法二:
分法一:
分法二:
20.(6分)由于保管不慎,小明把一道数学题染上了污渍,变成了“如图,在△ABC中
∠A=30°,tanB= ▲ ,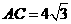 ,求AB的长”。这时小明去翻看了标准答案,显示AB=10.你能否帮助小明通过计算说明污渍部分的内容是什么?
,求AB的长”。这时小明去翻看了标准答案,显示AB=10.你能否帮助小明通过计算说明污渍部分的内容是什么?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com