7、 由一次函数，和轴围成的三角形与圆心在(0，1)、

　 半径为1的圆构成的图形覆盖的面积等于　　　 　．

6、 已知：○+○+○=100，(◎+◎)×○=100， □+○×◎×◎=79 .

　　 那么□=　　　 　.

5. 2010年上海世博会的园区规划用地面积约为5280000m²．将5280000用科学记数法表示为　　　　　　 ．

4.根据如图所示的计算程序，若输入的值x =－1，

　 则输出的值y = 　 ．

3.函数，．当时，x的范围是　(　)

A.．x＜－1　　　　 　B．－1＜x＜2　　

　C．x＜－1或x＞2　　　 D．x＞2

2. 如图，已知ABCD，∠A=45°，AD=4，以AD为直径的半圆O与

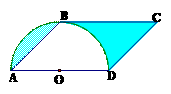BC相切于点B，则图中阴影部分的面积为

A．4　　　 B．π+2　　　 C．4　　　　 D．2

1.如果是有理数，式子的最小值是(　　　 )

A．2　　　　　 　B．3　　　　　 　C．4　　　　　 　D．5

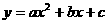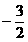23. (11分)已知：抛物线(a≠0)的顶点M的坐标为(1,－2)与y轴交于点C(0，)，与x轴交于A、B两点(A在B的左边).

(1)求此抛物线的表达式；

(2)点P是线段OB上一动点(不与点B重合)，点Q在线段BM上移动且∠MPQ＝45°，设线段OP＝x，MQ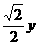＝₁，求y₁与x的函数关系式，并写出自变量x的取值范围；

(3)①在(2)的条件下是否存在点P，使△PQB是PB为底的等腰三角形，若存在试求点Q的坐标，若不存在说明理由；

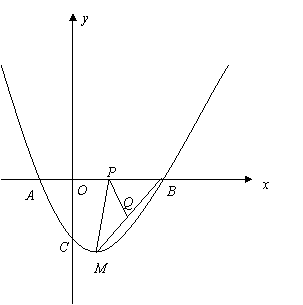②在(1)中抛物线的对称轴上是否存在点F，使△BMF是等腰三角形，若存在直接写出所有满足条件的点F的坐标.

22.(10分)如图，在梯形ABCD中，AB∥DC，∠ABC＝90°，AB＝2，BC＝4，tan∠ADC＝2.

(1)求证：DC＝BC；

(2)E是梯形内一点，连接DE、CE，将△DCE绕点C顺时针旋转90°，得△BCF，连接EF.判断EF与CE的数量关系，并证明你的结论；

(3)在(2)的条件下，当CE＝2BE，∠BEC＝135°时，求cos∠BFE的值.

21.(10分)如图，双曲线与直线x＝k相交于点P，过点P作PA⊥y轴于A，y轴上的点A₁、A₂、A₃……An的坐标是连续整数，分别过A₁、A₂……An作x轴的平行线于双曲线(x＞0)及直线x＝k分别交于点B₁、B₂，……Bn，C₁、C₂，……Cn.

(1)求A的坐标；

(2)求及的值；

(3)猜想的值(直接写答案).