5.　 若菱形两条对角线的长分别为6和8，则这个菱形的边长为( ▲ )

A．5　　　 　 B．10 　　　　 C．20　　　 　　　 D． 14

4.　已知三角形的两边长分别为3cm和8cm，则该三角形的第三边的长可能是( ▲ )

　 A．4cm　　　　　　 B．5cm　　　　　　 C．6cm　　　　　　 D．11cm

3.　若在实数范围内有意义，则x的取值范围是( ▲ )

A．x≥－2　　 B．x≠－2　　　　　 C．x≥2 　 D．x≠2

2.　下列运算正确的是( ▲ )

A．2x+3y＝5xy　　　　 　　　B．a³－a²＝a　

C．a－(a－b)＝－b　　　　　 D．(a－1)(a+2)＝a²+a－2

1.　计算－2+6的结果是( ▲ )

A．－8　　　 B．8　　　 C．－4　　　 D．4

26.(14分)如图，在平面直角坐标系中，O为坐标原点，⊙C的圆心坐标为，

半径为．函数y＝－x+2的图象与x轴交于点A，与y轴交于点B，点P为AB上一

动点

(1)连接CO，求证：CO⊥AB；

(2)若△POA是等腰三角形，求点P的坐标；

(3)当直线PO与⊙C相切时，

①求∠POA的度数；

②当直线PO与⊙C相交时，设交点为E、F，点M为线段EF的中点，令PO＝t，MO＝s，求s与t之间的函数关系，并写出t的取值范围．

2011年福建省泉州市毕业、升学考试数学模拟试题

25.(13分)如图，已知抛物线y＝－x²+x+4交x轴的正半轴于点A，交y轴于

点B．

(1)求A、B两点的坐标，并求直线AB的解析式；

(2)设P(x，y)(x＞0)是直线y＝x上的一点，Q是OP的中点(O是原点)，以PQ为对角线作正方形PEQF，若正方形PEQF与直线AB有公共点，求x的取值范围；

(3)在(2)的条件下，记正方形PEQF与△OAB公共部分的面积为S，求S关于x的函数解析式，并探究S的最大值．

24.(9分)某企业在生产甲、乙两种节能产品时需用A、B两种原料，生产每吨节

能产品所需原料的数量如下表所示：

本试卷由无锡市天一实验学校金杨建录制 QQ：623300747．转载请注明！

销售甲、乙两种产品的利润(万元)与销售量(吨)之间的函数关系如图所示．已知该企业生产了甲种产品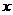吨和乙种产品吨，共用去A原料200吨．

(1)写出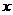与满足的关系式；

(2)为保证生产的这批甲种、乙种产品售后的总利润不少于220万元，那么至少要用B原料多少吨？

23.(9分) 如图，M为线段AB的中点，AE与BD交于点C，∠DME＝∠A＝∠B＝α，

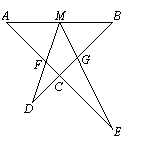且DM交AC于F，ME交BC于G．

(1)写出图中两对相似三角形；

(2)连结FG，如果α＝45°，AB＝，AF＝3，求FG的长．

22. ( 9分)在一个不透明的盒子里，装有三个分别写有数字6，2，7的小球，它们的形状、大小、质地等完全相同，先从盒子里随机取出一个小球，记下数字后放回盒子，摇匀后再随机取出一个小球，记下数字．求下列事件的概率：

(1)两次取出小球上的数字相同；

(2)两次取出小球上的数字之和大于10．