
题目列表(包括答案和解析)
(2)如果初三全年级同学的体育达标率不低于90%,则全年级同学人数不超过多少人?
19.(9分)小明在探究问题“正方形ABCD内一点E到A、B、C三点的距离之和的最小值”时, 由于EA、EB、EC比较分散,不便解决.于是将 绕点B逆时针旋转
绕点B逆时针旋转 得
得 ,联结EE′.
,联结EE′.
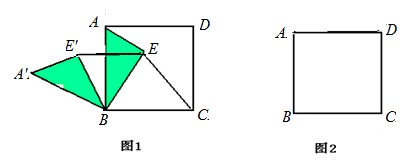
(1)小明得到的 是什么三角形?(直接写出结果,不必说出理由)
是什么三角形?(直接写出结果,不必说出理由)
(2)图1中联结A′C,试比较AE+BE+CE与A′C的大小.
(3)当点E在正方形ABCD内移动时,猜测AE+BE+CE有无最小值?如有利用图2画出符合题意的图示并说出理由;如果不存在最小值,简述理由.
18.(9分)初三(1)班课题小组对本校初三年级全体同学的1000米体育达标(体育成绩60分以上,含60分)情况进行调查.他们对本班50名同学的体育达标情况和其余班级同学的体育达标情况分别进行调查,数据统计如下:

说明:每组成绩的取值范围中,含最低值,不含最高值.
根据以上统计图,请解答下面问题:
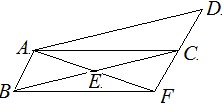
17.(9分)如图,在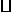
 中,
中, 为
为 的中点,连接
的中点,连接 并延长交
并延长交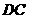 的延长线于点
的延长线于点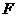 .
.
(1)求证: ;
;
(2)当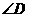 与
与 满足什么数量关系时,四边形
满足什么数量关系时,四边形 是矩形,并说明理由.
是矩形,并说明理由.
16.(8分)先化简,再求值: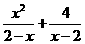 ,其中
,其中 .
.
15.如图,AB为半圆O的直径,C是半圆上一点,且∠COA=60°,设扇形AOC、△COB、弓形BmC的面积为S1、S2、S3,则它们之间面积最大的是__________.
14.两圆有多种位置关系,图中不存在的位置关系是 .


|
13.小明的作业本上有以下四题:①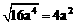 ;②
;②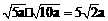 ;③
;③ ;④
;④ .做错的题是_______.
.做错的题是_______.
12.已知抛物线 经过点(1,2)与(
经过点(1,2)与(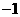 ,4),
,4),
则a+c的值是 .
11.如图,圆锥的主视图是等边三角形,圆锥的底面半径为2cm,
 假若点B有一蚂蚁只能沿圆锥的表面爬行,它要想吃到母线AC
假若点B有一蚂蚁只能沿圆锥的表面爬行,它要想吃到母线AC
的中点P处的食物,那么它爬行的最短路程是________cm.
10.平面直角坐标系中,点 、
、 、
、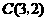 、
、 在
在 上,在图中点
上,在图中点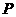 的坐标是 .
的坐标是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com