
题目列表(包括答案和解析)
2.分解因式:xy2-x=__________.
1.3的平方根是_________.
24.(14分)如图,已知抛物线 经过点
经过点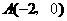 ,抛物线的顶点为
,抛物线的顶点为 ,过
,过 作射线OM∥AD.过顶点
作射线OM∥AD.过顶点 平行于
平行于 轴的直线交射线
轴的直线交射线 于点
于点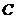 ,
, 在
在 轴正半轴上,连结
轴正半轴上,连结 .
.
(1)求该抛物线的解析式;(3分)
 (2)若动点
(2)若动点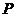 从点
从点 出发,以每秒1个长度单位的速度沿射线
出发,以每秒1个长度单位的速度沿射线 运动,设点
运动,设点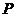 运动的时间为
运动的时间为 .问当
.问当 为何值时,四边形
为何值时,四边形 分别为平行四边形?直角梯形?等腰梯形?(6分)
分别为平行四边形?直角梯形?等腰梯形?(6分)
图(1)

备用图
(3)若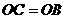 ,动点
,动点 和动点
和动点 分别从点
分别从点 和点
和点 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿
同时出发,分别以每秒1个长度单位和2个长度单位的速度沿 和
和 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
 ,连接
,连接 ,当
,当 为何值时,四边形
为何值时,四边形 的面积最小?并求出最小值及此时
的面积最小?并求出最小值及此时 的长.(5分)
的长.(5分)

23.(12分)如图①,平面直角坐标系中,已知C(0,10),点P、Q同时从点O出发,在线段OC上做往返匀速运动,设运动时间为t(s),点P、Q离开点O的距离为S,图②中线段OA、OB(A、B都在格点上)分别表示当0≤t≤6时P、Q两点离开点O的距离S与运动时间t(s)的函数图像.
⑴请在图②中分别画出当6≤t≤10时P、Q两点离开点O的距离S与运动时间t(s)的函数图像.(3分)
⑵求出P、Q两点第一次相遇的时刻.(3分)

 ⑶如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围) .(6分)
⑶如图①,在运动过程中,以OP为一边画正方形OPMD,点D在x轴正半轴上,作QE∥PD交x轴于E,设△PMD与△OQE重合部分的面积为y,试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围) .(6分)
22.(8分)如图,在一次课外数学实践活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,
已知DF=14m,EF=15m,求旗杆CD高.(结果精确到0.1m,参考数据: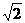 ≈1.41,
≈1.41, ≈1.73)
≈1.73)

21.(8分)如图,在△ABC中,AB=AC,D是BC中点,AE平分∠BAD交BC于点E,点O是AB上一点,⊙O过A、E两点, 交AD于点G,交AB于点F.
 (1)求证:BC与⊙O相切;
(1)求证:BC与⊙O相切;
(2)当∠BAC=120°时,求证: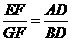 .
.
20. (8分)黄冈市为了更好地治理遗爱湖水质,保护环境,市治污公司决定购买10台,污水处理设备,现有A,B两种型号的设备,其中每台的价格,同处理污水量如下表:
|
|
A型 |
B型 |
|
价格(万元/台) |
a |
b |
|
处理污水量(吨/月) |
240 |
200 |
经调查:购买一台A型号设备比购买一台B型号设备多2万元,购买2台A型设备比购买3台B型号设备少6万元.
(1)求a ,b的值.
(2)经预算:使治污公司购买污水处理设备的资金不超过105万元,若每月要求处理遗爱湖的污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
19.(7分)双休日,甲、乙、丙三人去A、B两超市购物,如果三人去A、B两超市的机会均等.
(1)用画树状图或列表的方法表示出三人去超市的所有等可能结果;
(2)求出一人去A超市两人去B超市的概率.
18.(7分)如图,四边形ABCD中,∠A=90°,AD∥BC,BE⊥CD于E交AD的延长线于F,DC=2AD,AB=BE.
⑴求证:AD=DE.
⑵求证:四边形BCFD是菱形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com