
题目列表(包括答案和解析)
1、-8的立方根是
A、7
B、 -2 C、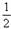 D、
D、
28.(本题满分12分)如图,在Rt△ABC中,∠B=90°,AB=1,BC= ,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
(1)求AE的长度;
 (2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.
解:(1)在Rt△ABC中,由AB=1,BC= 得 AC=
得 AC=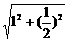 =
=
∵BC=CD,AE=AD
∴AE=AC-AD= .
.
(2)∠EAG=36°,理由如下:
∵FA=FE=AB=1,AE=
∴ =
=
∴△FAE是黄金三角形
∴∠F=36°,∠AEF=72°
∵AE=AG,FA=FE
∴∠FAE=∠FEA=∠AGE
∴△AEG∽△FEA
∴∠EAG=∠F=36°.
江苏省宿迁市2011年初中暨升学考试数学试题
27. (本题满分12分)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(本题满分12分)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
解:(1)∵四边形ABCD是正方形
∴∠A=∠B=∠D=90°,AD=AB
∵QE⊥AB,MF⊥BC
∴∠AEQ=∠MFB=90°
∴四边形ABFM、AEQD都是矩形
∴MF=AB,QE=AD,MF⊥QE
又∵PQ⊥MN
∴∠EQP=∠FMN
又∵∠QEP=∠MFN=90°
∴△PEQ≌△NFM.
(2)∵点P是边AB的中点,AB=2,DQ=AE=t
∴PA=1,PE=1-t,QE=2
由勾股定理,得PQ= =
=
∵△PEQ≌△NFM
∴MN=PQ=
又∵PQ⊥MN
∴S=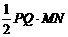 =
= =
= t2-t+
t2-t+
∵0≤t≤2
∴当t=1时,S最小值=2.
综上:S= t2-t+
t2-t+ ,S的最小值为2.
,S的最小值为2.
26.(本题满分10分)如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y= (x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(1)判断P是否在线段AB上,并说明理由;
(2)求△AOB的面积;
(3)Q是反比例函数y= (x>0)图象上异于点P的另一点,请以Q为圆心,QO
(x>0)图象上异于点P的另一点,请以Q为圆心,QO
半径画圆与x、y轴分别交于点M、N,连接AN、MB.求证:AN∥MB.
解:(1)点P在线段AB上,理由如下:
 ∵点O在⊙P上,且∠AOB=90°
∵点O在⊙P上,且∠AOB=90°
∴AB是⊙P的直径
∴点P在线段AB上.
(2)过点P作PP1⊥x轴,PP2⊥y轴,由题意可知PP1、PP2
是△AOB的中位线,故S△AOB= OA×OB=
OA×OB= ×2 PP1×PP2
×2 PP1×PP2
∵P是反比例函数y= (x>0)图象上的任意一点
(x>0)图象上的任意一点
∴S△AOB= OA×OB=
OA×OB= ×2 PP1×2PP2=2 PP1×PP2=12.
×2 PP1×2PP2=2 PP1×PP2=12.
 (3)如图,连接MN,则MN过点Q,且S△MON=S△AOB=12.
(3)如图,连接MN,则MN过点Q,且S△MON=S△AOB=12.
∴OA·OB=OM·ON
∴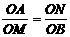
∵∠AON=∠MOB
∴△AON∽△MOB
∴∠OAN=∠OMB
∴AN∥MB.
25.(本题满分10分)某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
(1)有月租费的收费方式是 ▲ (填①或②),月租费是 ▲ 元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
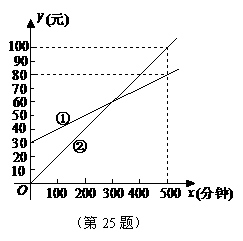 (3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
解:(1)①;30;
(2)设y有=k1x+30,y无=k2x,由题意得
 ,解得
,解得
故所求的解析式为y有=0.1x+30; y无=0.2x.
(3)由y有=y无,得0.2x=0.1x+30,解得x=300;
当x=300时,y=60.
故由图可知当通话时间在300分钟内,选择通话方式②实惠;当通话时间超过300分钟时,选择通话方式①实惠;当通话时间在300分钟时,选择通话方式①、②一样实惠.
24.(本题满分10分)在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
解:(1)∵
|
|
1 |
2 |
3 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
|
3 |
(3,1) |
(3,2) |
(3,3) |
∴点M坐标的所有可能的结果有九个:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)、(3,3).
(2)P(点M在直线y=x上)=P(点M的横、纵坐标相等)=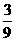 =
=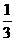 .
.
(3)∵
|
|
1 |
2 |
3 |
|
1 |
2 |
3 |
4 |
|
2 |
3 |
4 |
5 |
|
3 |
4 |
5 |
6 |
∴P(点M的横坐标与纵坐标之和是偶数)= .
.
23.(本题满分10分)如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取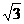 =1.732,结果精确到1m)
=1.732,结果精确到1m)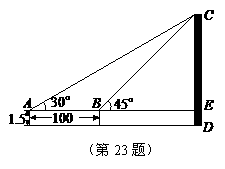
解:设CE=xm,则由题意可知BE=xm,AE=(x+100)m.
在Rt△AEC中,tan∠CAE= ,即tan30°=
,即tan30°=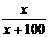
∴ ,3x=
,3x= (x+100)
(x+100)
解得x=50+50 =136.6
=136.6
∴CD=CE+ED=(136.6+1.5)=138.1≈138(m)
答:该建筑物的高度约为138m.
22.(本题满分8分)省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
|
|
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
|
甲 |
10 |
8 |
9 |
8 |
10 |
9 |
|
乙 |
10 |
7 |
10 |
10 |
9 |
8 |
(1)根据表格中的数据,计算出甲的平均成绩是 ▲ 环,乙的平均成绩是 ▲ 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2= [
[ ])
])
解:(1)9;9.
(2)s2甲=
=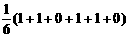 =
= ;
;
s2乙=
= =
=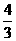 .
.
(3)推荐甲参加全国比赛更合适,理由如下:两人的平均成绩相等,说明实力相当;但甲的六次测试成绩的方差比乙小,说明甲发挥较为稳定,故推荐甲参加比赛更合适.
21.(本题满分8分)已知实数a、b满足ab=1,a+b=2,求代数式a2b+ab2的值.
解:当ab=1,a+b=2时,原式=ab(a+b)=1×2=2.
20.(本题满分8分)解不等式组
解:不等式①的解集为x>-1;
不等式②的解集为x+1<4
x<3
故原不等式组的解集为-1<x<3.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com