3．分解因式2x²-4x+2的最终结果是　　　　　　　　　　　　　　　　 (　 ▲　 )

　 A．2x(x－2)　　 B．2(x²－2x+1)　　 C．2(x－1)² 　D．(2x－2)²

[答案]C．

[考点]因式分解。

[分析]利用提公因式法和运用公式法，直接得出结果

2．若a>b，则　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 ▲　 )

　 A．a>－b　　 B．a<－b　　 C．－2a>－2b　　 D．－2a<－2b

[答案]D．

[考点]不等式。

[分析]利用不等式的性质，直接得出结果

1．︳－3︳的值等于　　　　　　　　　　　　　　　　　　　　　　　 (　 ▲　 )

　 A．3　　 8．－3　　 C．±3　　 D．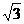

[答案]A．

[考点]绝对值。

[分析]利用绝对值的定义，直接得出结果

28.(2010江苏泰州，28，12分)在平面直角坐标系中，直线(k为常数且k≠0)分别交x轴、y轴于点A、B，⊙O半径为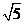个单位长度．

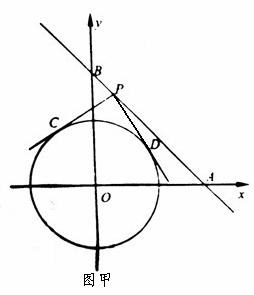
⑴如图甲，若点A在x轴正半轴上，点B在y轴正半轴上，且OA=OB．

①求k的值；

②若b=4，点P为直线上的动点，过点P作⊙O的切线PC、PD，切点分别为C、D，当PC⊥PD时，求点P的坐标．

⑵若，直线将圆周分成两段弧长之比为1∶2，求b的值．(图乙供选用)

[分析]⑴①由OA=OB=b ，不难求得k的值；②过P作x轴的垂线，设法求出点P到x轴与y轴的距离；⑵直线将圆周分成两段弧长之比为1∶2，可知其所对圆心角为120°，直线中∴直线与x轴交角的正切值为，充分理解这两层意思，再结合直角三角形将直线所经过的某一点的坐标求出，即得其解析式．

[答案]⑴①根据题意得：B的坐标为(0，b)，∴OA=OB=b，∴A的坐标为(b，0)，代入y＝kx+b得k＝－1.

②过P作x轴的垂线，垂足为F，连结OD.

∵PC、PD是⊙O的两条切线，∠CPD=90°，

∴∠OPD=∠OPC=∠CPD=45°，

∵∠PDO=90°，，∠POD=∠OPD＝45°，

∴OD＝PD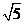＝，OP=.

∵P在直线y＝－x+4上，设P(m，－m+4)，则OF=m，PF=－m+4，

∵∠PFO=90°， OF²+PF²＝PO²，

∴ m²+ (－m+4)²＝()²，

解得m=1或3，

∴P的坐标为(1，3)或(3，1)

⑵分两种情形，y＝－x+，或y＝－x－。

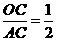直线将圆周分成两段弧长之比为1∶2，可知其所对圆心角为120°，如图，画出弦心距OC，可得弦心距OC=，又∵直线中∴直线与x轴交角的正切值为，即，∴AC=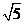，进而可得AO=，即直线与与x轴交于点(，0)．所以直线与y轴交于点(，0)，所以b的值为．

当直线与x轴、y轴的负半轴相交，同理可求得b的值为．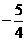

综合以上得：b的值为或．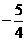

[涉及知识点]一次函数、勾股定理、圆的切线等知识的综合运用

[点评]中考题的最后一两道题俗称压轴题，主要考查学生的综合运用能力，包括知识综合、方法综合以及数学思想的综合运用，能较好地区分出不同数学水平的学生，保证区分结果的稳定性，从而确保试题具有良好的区分度，进而有利于高一级学校选拔新生．对我们学生而言要注意从简单的地方入手，将一些数学语言用自己熟悉的便于理解的即换一种语言表达出来，这些方法对解答综合题有一定的作用．

[推荐指数]★★★★

27．(2010江苏泰州，27，12分)如图，二次函数的图象经过点D，与x轴交于A、B两点．

⑴求的值；

⑵如图①，设点C为该二次函数的图象在x轴上方的一点，直线AC将四边形ABCD的面积二等分，试证明线段BD被直线AC平分，并求此时直线AC的函数解析式；

⑶设点P、Q为该二次函数的图象在x轴上方的两个动点，试猜想：是否存在这样的点P、Q，使△AQP≌△ABP？如果存在，请举例验证你的猜想；如果不存在，请说明理由．(图②供选用)

[分析]⑴将D点坐标代入二次函数解析式即可求出c的值；⑵要证明线段BD被直线AC平分，从“直线AC将四边形ABCD的面积二等分”来录求解题思路，不难发现S_△ABC=S_△ADC．通过面积法可得AC公共边上的两条高相等，再通过全等可得线段BD被直线AC平分；⑶通过逆向思考，假设存在这样的点P、Q，使△AQP≌△ABP，则可得AP平分∠QAB，通过画图可进一步确认其存在的可能性．

[答案]⑴ ∵抛物线经过点D()

∴

∴c=6.

⑵过点D、B点分别作AC的垂线，垂足分别为E、F，设AC与BD交点为M，

　∵AC 将四边形ABCD的面积二等分，即：S_△ABC=S_△ADC　 ∴DE=BF　

又∵∠DME=∠BMF， ∠DEM=∠BFE

∴△DEM≌△BFM

∴DM=BM　　 即AC平分BD

∵c=6.　 ∵抛物线为

∴A()、B()

∵M是BD的中点　 ∴M()

设AC的解析式为y=kx+b，经过A、M点

解得

直线AC的解析式为.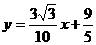

⑶存在．设抛物线顶点为N(0，6)，在Rt△AQN中，易得AN=，于是以A点为圆心，AB=为半径作圆与抛物线在x上方一定有交点Q，连接AQ，再作∠QAB平分线AP交抛物线于P，连接BP、PQ，此时由“边角边”易得△AQP≌△ABP．

[涉及知识点]二次函数、一次函数、解直角三角形及其知识的综合运用

[点评]一道题能涉及众多重点知识，既有代数的，又有几何的，又能考查到重要的数学思想、方法，这正是代数几何综合题的“本色”，综合性强，能力要求高，区分度大，决定了代数几何综合题历来被命题者所看重．从近几年的中考来看，不少试卷把其作为压轴题把关．在复习中要对这类问题引起足够重视，掌握这类问题的几种典型类型，加强这类问题的训练．

[推荐指数]★★★★

26.(2010江苏泰州，26，10分)保护生态环境，建设绿色社会已经从理念变为人们的行动．某化工厂2009年1 月的利润为200万元．设2009年1 月为第1个月，第x个月的利润为y万元．由于排污超标，该厂决定从2009年1 月底起适当限产，并投入资金进行治污改造，导致月利润明显下降，从1月到5月，y与x成反比例．到5月底，治污改造工程顺利完工，从这时起，该厂每月的利润比前一个月增加20万元(如图)．

⑴分别求该化工厂治污期间及治污改造工程完工后y与x之间对应的函数关系式．

⑵治污改造工程完工后经过几个月，该厂月利润才能达到2009年1月的水平？

⑶当月利润少于100万元时为该厂资金紧张期，问该厂资金紧张期共有几个月？

[分析]当1≤≤5时，图象是反比例函数的图象，设解析式将(1，200)代入即可求其解析式；当＞5时，是一次函数的图象，根据从这时起，该厂每月的利润比前一个月增加20万元，可得一次函数解析式．利润少于100万元要分别从反比例函数和一次函数中求对应的月份．

[答案]⑴①当1≤≤5时，设，把(1，200)代入，得，即；②当时，，所以当＞5时，；

⑵当y=200时，20x-60=200，x=13，所以治污改造工程顺利完工后经过13-5=8个月后，该厂利润达到200万元；

⑶对于，当y=100时，x=2；对于y=20x-60，当y=100时，x=8，所以资金紧张的时间为8-2=6个月．

[涉及知识点]反比例函数、一次函数的性质及应用

[点评]本题是一道反比例函数及一次函数有关的图象信息题，巧妙地这两个函数结合在一起，考查了同学们对数学知识的实际应用能力．图象信息题的主要特点是已知条件陷臧在给出的图象中，解决此类问题的关键是读懂图象，从图象中找出解题所需要的相关条件，然后正确求解．

[推荐指数]★★★★

25.(2010江苏泰州，25，10分)庞亮和李强相约周六去登山，庞亮从北坡山脚C处出发，以24米/分钟的速度攀登，同时，李强从南坡山脚B处出发．如图，已知小山北坡的坡度，山坡长为240米，南坡的坡角是45°．问李强以什么速度攀登才能和庞亮同时到达山顶A？(将山路AB、AC看成线段，结果保留根号)

[分析]由题意通过作辅助线构造两个共边的直角三角形，再由解直角三角形的知识可求得山坡AB的长，要使得李强和庞亮同时到达山项，只要将庞亮登到山项的时间算出即可得李强的速度．

[答案]过点A作AD⊥BC于点D，

在Rt△ADC中，由得tanC=∴∠C=30°∴AD=AC=×240=120(米)

在Rt△ABD中，∠B=45°∴AB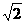＝AD＝120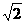(米)

120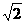÷(240÷24)＝120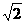÷10＝12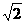(米/分钟)

答：李强以12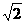米/分钟的速度攀登才能和庞亮同时到达山顶A．

[涉及知识点]解直角三角形

[点评]转化是解直角三解形的关键，解斜三角形一般要通过辅助线把斜三角形转化为几个直角三角形，再解直角三角形．

[推荐指数]★★★★★

24.(2010江苏泰州，24，10分)玉树地震后，全国人民慷慨解囊，积极支援玉树人民抗震救灾，他们有的直接捐款，有的捐物．国家民政部、中国红十字会、中华慈善总会及其他基金会分别接收了捐赠，青海省也直接接收了部分捐赠．截至5月14日12时，他们分别接收捐赠(含直接捐款数和捐赠物折款数)的比例见扇形统计图(图①)，其中，中华慈善总会和中国红十字会共接收捐赠约合人民币15.6亿元．请你根据相关信息解决下列问题：

(1)其他基金会接收捐赠约占捐赠总数的百分比是　　　　 ；

(2)全国接收直接捐款数和捐物折款数共计约　　　　 亿元；

(3)请你补全图②中的条形统计图；

(4)据统计，直接捐款数比捐赠物折款数的6倍还多3亿元，那么直接捐款数和捐赠物折款数各多少亿元？

[分析]⑴1-33%-33%-13%-17%＝4%，故应填4%；⑵因为中华慈善总会和中国红十字会共接收捐赠约合人民币15.6亿元，而这两家机构点捐赠的百分比为(13%+17%)＝30%，所以全国接收的捐款数和捐物折款数为：15.6÷30%＝52亿，应填52亿．⑶由13%×52=6.76亿，可知中华慈善总会所受赠款物的条形高度．⑷小题是一道简单的一元一次方程的应用题，只要抓住总接收的捐款数和和捐物折款数为52亿即可列出方程．

[答案]⑴4%；⑵52亿；⑶补全图如下：

⑷设直接捐款数为x，则捐赠物折款数为：(52－x)

依题意得：x＝6(52－x)+3

解得x＝45(亿)

(52－x)＝52－45＝7(亿)

答：直接捐款数和捐赠物折款数分别为45亿，7亿元．．

[涉及知识点]扇形统计图　 条形统计图

[点评]对数据进行整理和分析，要能从统计图中获取信息和数据，并作出合理的判断和预测，有些题目还要求对由数据得到的结论进行合理的质疑．这类题型充分展现了数学的实效性．解决这类题要以生活经验寻求基本的数量关系，要有针对性，要克服光靠图象，不加数学分析的主观臆断．

[推荐指数]★★★★★

23.(2010江苏泰州，23，10分)近期以来，大蒜和绿豆的市场价格离奇攀升，网民戏称为“蒜你狠”、“豆你玩”．以绿豆为例，5月上旬某市绿豆的市场价已达16元/千克．市政府决定采取价格临时干预措施，调进绿豆以平抑市场价格．经市场调研预测，该市每调进100吨绿豆，市场价格就下降1元/千克．为了即能平抑绿豆的市场价格，又要保护豆农的生产积极性，绿豆的市场价格控制在8元/千克到10元/千克之间(含8元/千克和10元/千克)．问调进绿豆的吨数应在什么范围内为宜？

[分析]理解了“每调进100吨绿豆，市场价格就下降1元/千克”，即“每调进1吨绿豆，市场价格就下降元/千克”，并比较容易列不等式组了．

[答案]设调进绿豆x吨，根据题意，得

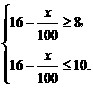　解得 600≤x≤800.

答：调进绿豆的吨数应不少于600吨，并且不超过800吨．

[涉及知识点]一元一次不等式组的应用

[点评]本例是不等式组在实际生活中的综合运用，侧重考查如何把生活问题转化为数学问题的能力，建立不等式模型，即“数学建模”． 从近两年的中考题来看，一元一次不等式(组)的实际应用题比以前要有所增加，其呈现的方式通常是与方程、一次函数等知识结合来求解．另外还常常辅以图表来说明有关信息，我们要抓住相等或不等的数量关系，结合图表观察、分析、猜想、归纳从而找到解题的最佳途径．

[推荐指数]★★★★

22.(2010江苏泰州，22，8分)如图，四边形ABCD是矩形，∠EDC=∠CAB，∠DEC=90°．

(1)求证：AC∥DE；

(2)过点B作BF⊥AC于点F，连结EF，试判断四边形BCEF的形状，并说明理由．

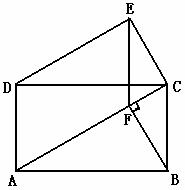
[分析](1)要证AC∥DE，设法证两个内错角相等，由已知∠EDC=∠CAB，再由矩形利用两边平行将∠ACD作为中间量进行转化；(2)可先猜想四边形BCEF是平行四边形，设法证EF、BC与AD的关系运用EF、BC平行且相等可得证．

[答案]⑴在矩形ABCD中，AC∥DE，∴∠DCA=∠CAB，∵∠EDC=∠CAB，

∴∠DCA=∠EDC，∴AC∥DE；

⑵四边形BCEF是平行四边形．

理由：由∠DEC=90°，BF⊥AC，可得∠AFB=∠DEC=90°，

又∠EDC=∠CAB，AB=CD，

∴△DEC≌△AFB，∴DE=AF，由⑴得AC∥DE，

∴四边形AFED是平行四边形，∴AD∥EF且AD=EF，

∵在矩形ABCD中，AD∥BC且AD=BC，

∴EF∥BC且EF=BC，

∴四边形BCEF是平行四边形．

[涉及知识点]矩形的性质 平行四边形的判定 全等三角形的判定

[点评]从中考试卷来看，平行四边形这一节不会有很复杂的证明题，主要考查平行四边形的性质特征及判别方法综合运用. 掌握这部分内容，首先搞清平行四边形与矩形、菱形、 正方形之间的包含关系．注重把握特殊平行四边形与一般平行四边形的异、同点，才能准确地、灵活地运用．

[推荐指数]★★★★★