17、(2011•滨州)将矩形ABCD沿AE折叠，得到如图所示图形．若∠CED′=56°，则∠AED的大小是　62　°．

考点：翻折变换(折叠问题)。

专题：操作型；数形结合。

分析：易得∠DED′的度数，除以2即为所求角的度数．

解答：解：∵∠CED′=56°，

∴∠DED′=180°﹣∠56°=124°，

∵∠AED=∠AED′，

∴∠AED=∠DED′=62°．

故答案为：62．

点评：考查翻折变换问题；用到的知识点为：翻折前后得到的角相等．

16、(2011•滨州)在等腰△ABC中，∠C=90°，则tanA=　1　．

考点：特殊角的三角函数值；等腰直角三角形。

分析：根据△ABC是等腰三角形，∠C=90°，求出∠A=∠B=45°，从而求出角A的正切值．

解答：解：∵△ABC是等腰三角形，∠C=90°，

∴∠A=∠B=45°，

∴tanA=tan45°=1，

故答案为1．

点评：本题涉及到的知识点有：等腰直角三角形、特殊角的三角函数值，解题时牢记特殊角的三角函数值．

15、(2011•滨州)边长为6cm的等边三角形中，其一边上高的长度为　3cm　．

考点：等边三角形的性质；勾股定理。

专题：应用题。

分析：根据等边三角形三角都是60°利用三角函数可求得其高．

解答：解：∵△ABC是等边三角形，

∴∠B=60°，

∵AB=6cm，

∴AD=3cm．

故答案为：3cm．

点评：本题主要考查学生对等边三角形的性质的理解及运用能力，比较简单．

14、(2011•滨州)若x=2是关于x的方程x²﹣x﹣a²+5=0的一个根，则a的值为　±．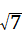

考点：一元二次方程的解。

分析：方程的解就是能使方程左右两边相等的未知数的值，把x=2代入方程，即可得到一个关于a的方程，即可求得a的值．

解答：解：把x=2代入方程x²﹣x﹣a²+5=0得：

4﹣2﹣a²+5=0，

解得：a=±．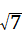

故答案为：±．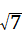

点评：本题主要考查了方程的解得定义，是需要掌握的基本内容．

13、(2008•贵阳)分解因式：x²﹣4=　(x+2)(x﹣2)　．

考点：因式分解-运用公式法。

分析：直接利用平方差公式进行因式分解即可．

解答：解：x²﹣4=(x+2)(x﹣2)．

点评：本题考查了平方差公式因式分解．能用平方差公式进行因式分解的式子的特点是：两项平方项，符号相反．

12、(2011•滨州)如图，在一张△ABC纸片中，∠C=90°，∠B=60°，DE是中位线，现把纸片沿中位线DE剪开，计划拼出以下四个图形：①邻边不等的矩形；②等腰梯形；③有一个角为锐角的菱形；④正方形．那么以上图形一定能被拼成的个数为(　)

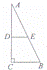
　　 A、1　　　　 B、2

　　 C、3　　　　 D、4

考点：三角形中位线定理。

专题：作图题。

分析：将该三角形剪成两部分，拼图使得△ADE和直角梯形BCDE不同的边重合，即可解题．

解答：解：①使得CE与AE重合，即可构成邻边不等的矩形，如图：

∵∠C=60°，

∴AB=BC，

∴BD≠BC．

②使得BD与AD重合，即可构成等腰梯形，如图：

③使得BD与DE重合，即可构成有一个角为锐角的菱形，如图：

故计划可拼出①②③．

故选C．

点评：本题考查了三角形中位线定理的运用，考查了三角形中位线定理的性质，本题中求证BD≠BC是解题的关键．

11、(2011•滨州)如图．在△ABC中，∠B=90°，∠A=30°，AC=4cm，将△ABC绕顶点C顺时针方向旋转至△A'B'C的位置，且A、C、B'三点在同一条直线上，则点A所经过的最短路线的长为(　)

　　 A、　　　　 B、8cm

　　 C、　　 D、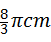

考点：旋转的性质；弧长的计算。

分析：点A所经过的最短路线是以C为圆心、CA为半径的一段弧线，运用弧长公式计算求解．

解答：解：∵∠B=90°，∠A=30°，A、C、B'三点在同一条直线上，

∴∠ACA′=120°．

又AC=4，

∴L=(cm)．

故选D．

点评：此题考查了性质的性质和弧长的计算，搞清楚点A的运动轨迹是关键．难度中等．

9、(2011•滨州)在△ABC中，∠C=90°，∠A=72°，AB=10，则边AC的长约为(精确到0.1)(　)

　　 A、9.1　　　 B、9.5

　　 C、3.1　　　 D、3.5

考点：解直角三角形。

专题：计算题。

分析：在Rt△ABC中，根据三角函数的定义，易得AB、AC及∠A的关系，进而计算可得答案．

解答：解：根据题意

，

在Rt△ABC中，有cosA=，sinA=；

则AC=AB•cosA=10×cos72°≈3.1；

故选C．

点评：本题考查了解直角三角形的应用，要熟练掌握好边角之间的关系及三角函数的定义．

8、(2011•滨州)如图，在平面直角坐标系中，正方形ABCO的顶点A、C分别在y轴、x轴上，以AB为弦的⊙M与x轴相切．若点A的坐标为(0，8)，则圆心M的坐标为(　)

　　 A、(﹣4，5)　　　　 B、(﹣5，4)

　　 C、(5，﹣4)　　　　 D、(4，﹣5)

考点：垂径定理；坐标与图形性质；勾股定理；正方形的性质。

专题：证明题。

分析：过点M作MD⊥AB于D，连接AM．设⊙M的半径为R，因为四边形OABC为正方形，顶点A，C在坐标轴上，以边AB为弦的⊙M与x轴相切，若点A的坐标为(0，8)，所以DA=AB=4，DM=8﹣R，AM=R，又因△ADM是直角三角形，利用勾股定理即可得到关于R的方程，解之即可．

解答：解：过点M作MD⊥AB于D，交OC于点E．连接AM，设⊙M的半径为R．

∵以边AB为弦的⊙M与x轴相切，AB∥OC，

∴DE⊥CO，

∴DE是⊙M直径的一部分；

∵四边形OABC为正方形，顶点A，C在坐标轴上，点A的坐标为(0，8)，

∴OA=AB=CB=OC=8，DM=8﹣R；

∴AD=BD=4(垂径定理)；

在Rt△ADM中，

根据勾股定理可得AM²=DM²+AD²，

∴R²=(8﹣R)²+4²，∴R=5．

∴M(﹣4，5)．

故选D．

点评：本题考查了垂径定理、坐标与图形性质、勾股定理及正方形的性质．解题时，需仔细分析题意及图形，利用勾股定理来解决问题．