
题目列表(包括答案和解析)
22、(2011•泰安)化简: 的结果为 x﹣6 .
的结果为 x﹣6 .
考点:分式的混合运算。
专题:计算题。
分析:先将括号里面的通分合并同类项,然后将除法转换成乘法,约分化简得到最简代数式.
解答:解:原式=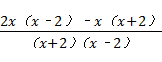 ×
×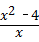
= ×
×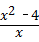
=x﹣6
故答案为:x﹣6
点评:本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.
21、(2011•泰安)方程2x2+5x﹣3=0的解是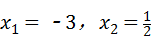 .
.
考点:解一元二次方程-因式分解法。
专题:因式分解。
分析:先把方程化为(x+3)(x﹣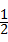 )=0的形式,再求出x的值即可.
)=0的形式,再求出x的值即可.
解答:解:原方程可化为:(x+3)(x﹣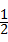 )=0,
)=0,
故x1=﹣3,x2=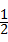 .
.
故答案为:x1=﹣3,x2=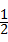 .
.
点评:本题考查的是解一元二次方程的因式分解法,能把原方程化为两个因式积的形式是解答此题的关键.
20、(2011•泰安)若二次函数y=ax2+bx+c的x与y的部分对应值如下表:
|
x |
﹣7 |
﹣6 |
﹣5 |
﹣4 |
﹣3 |
﹣2 |
|
y |
﹣27 |
﹣13 |
﹣3 |
3 |
5 |
3 |
则当x=1时,y的值为( )
A、5 B、﹣3
C、﹣13 D、﹣27
考点:待定系数法求二次函数解析式。
专题:计算题。
分析:由表可知,抛物线的对称轴为x=﹣3,顶点为(﹣3,5),再用待定系数法求得二次函数的解析式,再把x=1代入即可求得y的值.
解答:解:设二次函数的解析式为y=a(x﹣h)2+k,
∵h=﹣3,k=5,
∴y=a(x+3)2+5,
把(﹣2,3)代入得,a=﹣2,
∴二次函数的解析式为y=﹣2(x+3)2+5,
当x=1时,y=﹣27.
故选D.
点评:本题看出来用待定系数法求二次函数的解析式,抛物线是轴对称图形,对称轴为x=﹣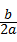 .
.
19、(2011•泰安)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )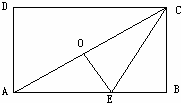
A、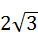 B、
B、
C、 D、6
D、6
考点:翻折变换(折叠问题);勾股定理。
专题:探究型。
分析:先根据图形翻折变换的性质求出AC的长,再由勾股定理及等腰三角形的判定定理即可得出结论.
解答:解:∵△CED是△CEB翻折而成,
∴BC=CD,BE=DE,
∵O是矩形ABCD的中心,
∴OE是AC的垂直平分线,AC=2BC=2×3=6,
∴AE=CE,
在Rt△ABC中,AC2=AB2+BC2,即62=AB2+32,解得AB=3 ,
,
在Rt△AOE中,设OE=x,则AE=3 ﹣x,
﹣x,
AE2=AO2+OE2,即(3 ﹣x)2=(3
﹣x)2=(3 )2+32,解得x=
)2+32,解得x= ,
,
∴AE=EC=3 ﹣
﹣ =2
=2 .
.
故选A.
点评:本题考查的是翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等的知识是解答此题的关键.
18、(2011•泰安)不等式组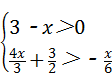 的最小整数解为( )
的最小整数解为( )
A、0 B、1
C、2 D、﹣1
考点:一元一次不等式组的整数解。
专题:计算题。
分析:首先解不等式组求得不等式的解集,然后确定解集中的最小整数值即可.
解答:解:解第一个不等式得:x<3;
解第二个不等式得:x>﹣1
故不等式组的解集是:﹣1<x<3.
故最小整数解是:0
故选:A.
点评:本题主要考查了不等式组的解法,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.
17、(2011•泰安)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
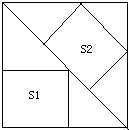
A、16 B、17
C、18 D、19
考点:相似三角形的判定与性质;正方形的性质。
专题:计算题。
分析:由图可得,S1的边长为3,由AC= BC,BC=CE=
BC,BC=CE= CD,可得AC=2CD,CD=2,EC=
CD,可得AC=2CD,CD=2,EC=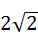 ;然后,分别算出S1、S2的面积,即可解答;
;然后,分别算出S1、S2的面积,即可解答;
解答:解:如图,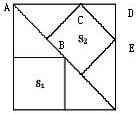 设正方形S2的边长为x,
设正方形S2的边长为x,
根据等腰直角三角形的性质知,AC= BC,BC=CE=
BC,BC=CE= CD,
CD,
∴AC=2CD,CD= =2,
=2,
∴EC2=22+22,即EC=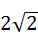 ;
;
∴S2的面积为 =8;
=8;
∵S1的边长为3,S1的面积为3×3=9,
∴S1+S2=8+9=17.
故选B.
点评:本题考查了正方形的性质和等腰直角三角形的性质,考查了学生的读图能力.
16、(2011•泰安)袋中装有编号为1,2,3的三个质地均匀、大小相同的球,从中随机取出一球记下编号后,放入袋中搅匀,再从袋中随机取出一球,两次所取球的的编号相同的概率为( )
A、 B、
B、
C、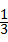 D、
D、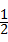
考点:列表法与树状图法。
分析:依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式即可求出该事件的概率.
解答:解:画树状图得:
∴一共有9种等可能的结果,
两次所取球的的编号相同的有3种,
∴两次所取球的的编号相同的概率为 =
=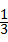 .
.
故选C.
点评:本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
15、(2011•泰安)如图,点F是▱ABCD的边CD上一点,直线BF交AD的延长线与点E,则下列结论错误的是( )

A、 B、
B、
C、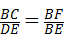 D、
D、
考点:平行线分线段成比例;平行四边形的性质。
分析:由四边形ABCD是平行四边形,可得CD∥AB,AD∥BC,CD=AB,AD=BC,然后平行线分线段成比例定理,对各项进行分析即可求得答案.
解答:解:∵四边形ABCD是平行四边形,
∴CD∥AB,AD∥BC,CD=AB,AD=BC,
∴ ,故A正确;
,故A正确;
∴ ,
,
∴ ,故B正确;
,故B正确;
∴ ,故C错误;
,故C错误;
∴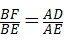 ,
,
∴ ,故D正确.
,故D正确.
故选C.
点评:本题考查平行线分线段成比例定理,找准对应关系,避免错选其他答案.
14、(2011•泰安)一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是( )
A、5π B、4π
C、3π D、2π
考点:圆锥的计算。
分析:半圆的面积就是圆锥的侧面积,根据半圆的弧长等于圆锥底面圆的周长,即可求得圆锥底面圆的半径,进而求得面积,从而求解.
解答:解:侧面积是: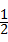 ×π×22=2π.
×π×22=2π.
底面的周长是2π.
则底面圆半径是1,面积是π.
则该圆锥的全面积是:2π+π=3π.
故选C.
点评:本题主要考查了圆锥的计算,正确理解圆锥的底面的周长等于展开图中扇形的弧长是解题的关键.
13、(2011•泰安)已知一次函数y=mx+n﹣2的图象如图所示,则m、n的取值范围是( )
A、m>0,n<2 B、m>0,n>2
C、m<0,n<2 D、m<0,n>2
考点:一次函数图象与系数的关系。
专题:探究型。
分析:先根据一次函数的图象经过二、四象限可知m<0,再根据函数图象与y轴交与正半轴可知n﹣2>0,进而可得出结论.
解答:解:∵一次函数y=mx+n﹣2的图象过二、四象限,
∴m<0,
∵函数图象与y轴交与正半轴,
∴n﹣2>0,
∴n>2.
故选D.
点评:本题考查的是一次函数的图象,即直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com