
题目列表(包括答案和解析)
2.如图,直线AB∥CD,∠A=70°,∠C=40°,
则∠E等于
A.30° B.40°
C.60° D.70°
请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一
个均记零分.
1.下列计算正确的是
A.a6÷a2=a3 B.a2+a3=a5
 C.(a2)3=a6
D.(a+b)2=a2+b2
C.(a2)3=a6
D.(a+b)2=a2+b2
29、(2011•泰安)已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.

考点:全等三角形的判定与性质;等腰直角三角形。
专题:证明题。
分析:(1)首先根据点D是AB中点,∠ACB=90°,可得出∠ACD=∠BCD=45°,判断出△AEC≌△CGB,即可得出AE=CG,
(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC,∠ACM=∠CBE=45°,得出△BCE≌△CAM,进而证明出BE=CM.
解答:解:(1)证明:∵点D是AB中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,又BF⊥CE,
∴∠CBG+∠BCF=90°,又∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
∴△AEC≌△CGB,
∴AE=CG,
(2)BE=CM,
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵AC=BC,∠ACM=∠CBE=45°,
∴△BCE≌△CAM,
∴BE=CM.
点评:本题主要考查了全等三角形的判定方法以及全等三角形对应边相等的性质,难度适中.
28、(2011•泰安)某商店经营一种小商品,进价为每件20元,据市场分析,在一个月内,售价定为25元时,可卖出105件,而售价每上涨1元,就少卖5件.
(1)当售价定为30元时,一个月可获利多少元?
(2)当售价定为每件多少元时,一个月的获利最大?最大利润是多少元?
考点:二次函数的应用。
专题:销售问题。
分析:(1)当售价定为30元时,可知每一件赚10元钱,再有售价定为25元时,可卖出105件,而售价每上涨1元,就少卖5件.可计算出一个月可获利多少元;
(2)设售价为每件x元时,一个月的获利为y元,得到y与x的二次函数关系式求出函数的最大值即可.
解答:解:(1)获利:(30﹣20)[105﹣5(30﹣25)]=800;
(2)设售价为每件x元时,一个月的获利为y元,
由题意,得y=(x﹣20)[105﹣5(x﹣25)]=﹣5x2+330x﹣4600=﹣5(x﹣33)2+845,
当x=33时,y的最大值为845,
故当售价定为33元时,一个月的利润最大,最大利润是845元.
点评:本题主要考查了二次函数的应用,能正确表示出月销售量是解题的关键.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.
27、(2011•泰安)已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.
(1)点F是DC上一点,连接EF,交AC于点O(如图1),求证:△AOE∽△COF;
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.

考点:相似三角形的判定;菱形的判定。
专题:证明题;数形结合。
分析:(1)由点E是BC的中点,BC=2AD,可证得四边形AECD为平行四边形,即可得△AOE∽△COF;
(2)连接DE,易得四边形ABED是平行四边形,又由∠ABE=90°,可证得四边形ABED是矩形,根据矩形的性质,易证得EF=GD=GE=DF,则可得四边形EFDG是菱形.
解答:(1)证明:∵点E是BC的中点,BC=2AD,
∴EC=BE=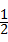 BC=AD,
BC=AD,
又∵AD∥DC,
∴四边形AECD为平行四边形,
∴AE∥DC,
∴∠AEO=∠CFO,∠EAO=∠FCO,
∴△AOE∽△COF;
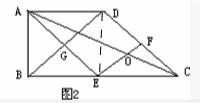 (2)证明:连接DE,
(2)证明:连接DE,
∵DE平行且等于BE,
∴四边形ABED是平行四边形,
又∠ABE=90°,
∴□ABED是矩形,
∴GE=GA=GB=GD=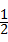 BD=
BD=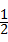 AE,
AE,
∴E、F分别是BC、CD的中点,
∴EF、GE是△CBD的两条中线,
∴EF=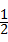 BD=GD,GE=
BD=GD,GE=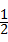 CD=DF,
CD=DF,
又GE=GD,
∴EF=GD=GE=DF,
∴四边形EFDG是菱形.
点评:此题考查了相似三角形的判定与性质,平行四边形的判定与性质,矩形与菱形的判定与性质等知识.此题综合性较强,难度适中,解题的关键是要注意数形结合思想的应用.
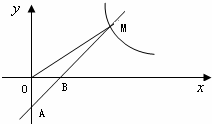
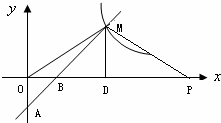
26、(2011•泰安)如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数 的图象在第一象限内的交点为M,若△OBM的面积为2.
的图象在第一象限内的交点为M,若△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.
考点:反比例函数与一次函数的交点问题。
专题:探究型。
分析:(1)根据一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)可得到关于b、k1的方程组,进而可得到一次函数的解析式,设M(m,n)作MD⊥x轴于点D,由△OBM的面积为2可求出n的值,将M(m,4)代入y=2x﹣2求出m的值,由M(3,4)在双曲线 上即可求出k2的值,进而求出其反比例函数的解析式;
上即可求出k2的值,进而求出其反比例函数的解析式;
(2)过点M(3,4)作MP⊥AM交x轴于点P,由MD⊥BP可求出∠PMD=∠MBD=∠ABO,再由锐角三角函数的定义可得出OP的值,进而可得出结论.
解答:(1)∵直线y=k1x+b过A(0,﹣2),B(1,0)两点
∴ ,
,
∴
∴已知函数的表达式为y=2x﹣2.(3分)
∴设M(m,n)作MD⊥x轴于点D
∵S△OBM=2,
∴ ,
,
∴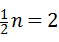
∴n=4(5分)
∴将M(m,4)代入y=2x﹣2得4=2m﹣2,
∴m=3
∵M(3,4)在双曲线 上,
上,
∴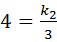 ,
,
∴k2=12
∴反比例函数的表达式为
(2)过点M(3,4)作MP⊥AM交x轴于点P,
∵MD⊥BP,
∴∠PMD=∠MBD=∠ABO
∴tan∠PMD=tan∠MBD=tan∠ABO=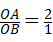 =2(8分)
=2(8分)
∴在Rt△PDM中,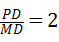 ,
,
∴PD=2MD=8,
∴OP=OD+PD=11
∴在x轴上存在点P,使PM⊥AM,此时点P的坐标为(11,0)(10分)
点评:本题考查的是反比例函数与一次函数的交点问题,涉及到的知识点为用待定系数法求一次函数与反比例函数的解析式、锐角三角函数的定义,熟知以上知识是解答此题的关键.
1.5x=90.
答:甲乙两车间每天加工零件分别为60个、90个.
点评:本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.本题需注意应设较小的量为未知数.
25、(2011•泰安)某工厂承担了加工2100个机器零件的任务,甲车间单独加工了900个零件后,由于任务紧急,要求乙车间与甲车间同时加工,结果比原计划提前12天完成任务.已知乙车间的工作效率是甲车间的1.5倍,求甲、乙两车间每天加工零件各多少个?
考点:分式方程的应用。
分析:先设甲车间每天加工零件x个,则乙车间每天加工零件1.5x个,由题意列分式方程即可得问题答案.
解答:解:设甲车间每天加工零件x个,则乙车间每天加工零件1.5x个.
根据题意,得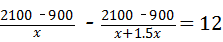 ,
,
解之,得x=60,
经检验,x=60是方程的解,符合题意,
24、(2011•泰安)甲、乙两人在5次体育测试中的成绩(成绩为整数,满分为100分)如下表,其中乙的第5次成绩的个位数被污损.
|
|
第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
|
甲 |
90 |
88 |
87 |
93 |
92 |
|
乙 |
84 |
87 |
85 |
98 |
9■ |
则乙的平均成绩高于甲的平均成绩的概率是 .
.
考点:概率公式;算术平均数。
专题:应用题。
分析:首先计算出甲的平均成绩,再根据乙的成绩在97,98,99的时候,平均成绩大于甲的成绩,随机事件概率的求法即可得出结果.
解答:解:甲的平均成绩为: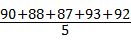 =90,
=90,
乙的被污损的成绩可能是90,91,92,93,94,95,96,97,98,99共10中可能,
乙的成绩为97,98,99的时候,平均成绩大于甲的成绩,
乙的平均成绩高于甲的平均成绩的概率是 .
.
故答案为: .
.
点评:本题考查了平均数的求法,以及随机事件概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)= ,难度适中.
,难度适中.
23、(2011•泰安)如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为 26° .
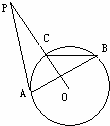
考点:切线的性质;圆周角定理。
分析:连接OA,则△PAO是直角三角形,根据圆周角定理即可求得∠POA的度数,进而根据直角三角形的性质求解.
解答:解: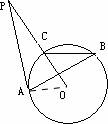 连接OA.
连接OA.
∴∠PAO=90°,
∵∠O=2∠B=64°,
∴∠P=90°﹣64°=26°.
故答案为:26°.
点评:本题主要考查了切线的性质,以及圆周角定理,正确利用定理,作出辅助线求得∠POA的度数是解题的关键.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com