
题目列表(包括答案和解析)
18、(2011•德州)2011年5月9日至14日,德州市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
|
等级 |
成绩(分) |
频数(人数) |
频率 |
|
A |
90-100 |
19 |
0.38 |
|
B |
75-89 |
m |
x |
|
C |
60-74 |
n |
y |
|
D |
60以下 |
3 |
0.06 |
|
合计 |
|
50 |
1.00 |
请你根据以上图表提供的信息,解答下列问题:
(1)m= 20 ,n= 8 ,x= 0.4 ,y= 0.16 ;
(2)在扇形图中,C等级所对应的圆心角是 57.6 度;
(3)如果该校九年级共有500名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?

考点:频数(率)分布表;用样本估计总体;扇形统计图。
专题:图表型。
分析:(1)让总人数50乘以相应的百分比40%可得m的值,x为相应百分比;让总人数50减去其余已知人数可得n的值,除以50即为y的值;
(2)让360乘以相应频率即为C等级所对应的圆心角;
(3)让总人数35000乘以AB两个等级的百分比的和即为所求的人数.
解答:解:(1)50×40%=20,0.4;50﹣19﹣20﹣3=8,8÷50=0.16;
故答案为:20,8,0.4,0.16(4分)
(2)0.16×360=57.6°,
故答案为57.6.(6分)
(3)由上表可知达到优秀和良好的共有19+20=39人,500× =390人.(8分)
=390人.(8分)
点评:考查有关识图问题;读懂图意是解决本题的关键;用到的知识点为:频数=总数×相应频率.
17、(2011•德州)解不等式组,并把解集在数轴上表示出来 .
.
考点:解一元一次不等式组;在数轴上表示不等式的解集。
专题:计算题;数形结合。
分析:分别解两个不等式得到x≥1;x<4.它们的公共部分即为原不等式组的解集,然后把解集表示在数轴上.
解答:解: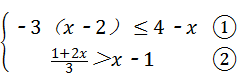
解不等式①,得x≥1;
解不等式②,得x<4.
∴1≤x<4.
在数轴上表示为: .
.
点评:本题考查了解不等式组的方法:分别解各不等式,然后写出它们的公共部分即为不等式组的解集.也考查了利用数轴表示不等式组的解集得方法.
16、(2011•德州)长为1,宽为a的矩形纸片( ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为
),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为 或
或 .
.
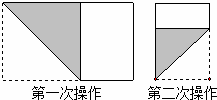
考点:一元一次方程的应用。
专题:几何图形问题;操作型。
分析:根据操作步骤,可知每一次操作时所得正方形的边长都等于原矩形的宽.所以首先需要判断矩形相邻的两边中,哪一条边是矩形的宽.当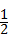 <a<1时,矩形的长为1,宽为a,所以第一次操作时所得正方形的边长为a,剩下的矩形相邻的两边分别为1﹣a,a.由1﹣a<a可知,第二次操作时所得正方形的边长为1﹣a,剩下的矩形相邻的两边分别为1﹣a,a﹣(1﹣a)=2a﹣1.由于(1﹣a)﹣(2a﹣1)=2﹣3a,所以(1﹣a)与(2a﹣1)的大小关系不能确定,需要分情况进行讨论.又因为可以进行三次操作,故分两种情况:①1﹣a>2a﹣1;②1﹣a<2a﹣1.对于每一种情况,分别求出操作后剩下的矩形的两边,根据剩下的矩形为正方形,列出方程,求出a的值.
<a<1时,矩形的长为1,宽为a,所以第一次操作时所得正方形的边长为a,剩下的矩形相邻的两边分别为1﹣a,a.由1﹣a<a可知,第二次操作时所得正方形的边长为1﹣a,剩下的矩形相邻的两边分别为1﹣a,a﹣(1﹣a)=2a﹣1.由于(1﹣a)﹣(2a﹣1)=2﹣3a,所以(1﹣a)与(2a﹣1)的大小关系不能确定,需要分情况进行讨论.又因为可以进行三次操作,故分两种情况:①1﹣a>2a﹣1;②1﹣a<2a﹣1.对于每一种情况,分别求出操作后剩下的矩形的两边,根据剩下的矩形为正方形,列出方程,求出a的值.
解答:解:由题意,可知当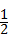 <a<1时,第一次操作后剩下的矩形的长为a,宽为1﹣a,所以第二次操作时正方形的边长为1﹣a,第二次操作以后剩下的矩形的两边分别为1﹣a,2a﹣1.此时,分两种情况:
<a<1时,第一次操作后剩下的矩形的长为a,宽为1﹣a,所以第二次操作时正方形的边长为1﹣a,第二次操作以后剩下的矩形的两边分别为1﹣a,2a﹣1.此时,分两种情况:
①如果1﹣a>2a﹣1,即a< ,那么第三次操作时正方形的边长为2a﹣1.
,那么第三次操作时正方形的边长为2a﹣1.
则2a﹣1=(1﹣a)﹣(2a﹣1),解得a= ;
;
②如果1﹣a<2a﹣1,即a> ,那么第三次操作时正方形的边长为1﹣a.
,那么第三次操作时正方形的边长为1﹣a.
则1﹣a=(2a﹣1)﹣(1﹣a),解得a= .
.
故答案为 或
或 .
.
点评:本题考查了一元一次方程的应用,解题的关键是分两种情况:①1﹣a>2a﹣1;②1﹣a<2a﹣1.分别求出操作后剩下的矩形的两边.
15、(2011•德州)在4张卡片上分别写有1-4的整数,随机抽取一张后放回,再随机地抽取一张,那么第二次取出的数字能够整除第一次取出的数字的概率是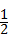 .
.
考点:列表法与树状图法。
专题:计算题。
分析:列举出所有情况,看第二次取出的数字能够整除第一次取出的数字的情况数占总情况数的多少即可.
解答:解: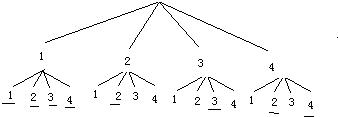
共有16种情况,第二次取出的数字能够整除第一次取出的数字的情况数有8种,
所以概率为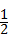 ,
,
故答案为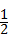 .
.
点评:考查概率的求法;用到的知识点为:概率=所求情况数与总情况数之比.得到第二次取出的数字能够整除第一次取出的数字的情况数是解决本题的关键.
14、(2011•德州)若x1,x2是方程x2+x﹣1=0的两个根,则x12+x22= 3 .
考点:根与系数的关系。
专题:计算题。
分析:先根据根与系数的关系求出x1+x2和x1•x2的值,再利用完全平方公式对所求代数式变形,然后把x1+x2和x1•x2的值整体代入计算即可.
解答:解:∵x1,x2是方程x2+x﹣1=0的两个根,
∴x1+x2=﹣ =﹣
=﹣ =﹣1,x1•x2=
=﹣1,x1•x2= =
= =﹣1,
=﹣1,
∴x12+x22=(x1+x2)2﹣2x1•x2=(﹣1)2﹣2×(﹣1)=1+2=3.
故答案是:3.
点评:本题考查了根与系数的关系、完全平方公式.解题的关键是先求出x1+x2和x1•x2的值.
13、(2011•德州)下列命题中,其逆命题成立的是 ①④ .(只填写序号)
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③如果两个实数相等,那么它们的平方相等;
④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
考点:命题与定理;实数的运算;角的概念;平行线的判定与性质;勾股定理;勾股定理的逆定理。
专题:推理填空题。
分析:把一个命题的条件和结论互换就得到它的逆命题,再分析逆命题是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
解答:解:A、两直线平行,同旁内角互补,正确,
B、如果两个角相等,那么它们是直角,错误,
C、如果两个实数的平方相等,那么这两个实数相等,错误,
D、一个三角形是直角三角形,那么三角形的三边长a,b,c满足a2+b2=c2,正确,
故答案为①④.
点评:本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题,难度适中.
12、(2011•德州)当 时,
时,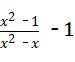 =
=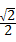 .
.
考点:分式的化简求值;二次根式的化简求值。
专题:计算题。
分析:先将分式的分子和分母分别分解因式,约分化简,然后将x的值代入化简后的代数式即可求值.
解答:解: ﹣1
﹣1
= ﹣1
﹣1
= ﹣
﹣
=
= ,将x=
,将x= 代入上式中得,
代入上式中得,
原式= =
= =
=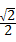 .
.
故答案为: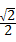 .
.
点评:本题主要考查分式求值方法之一:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.
11、(2011•德州)母线长为2,底面圆的半径为1的圆锥的侧面积为 2π .
考点:圆锥的计算。
专题:计算题。
分析:先计算出底面圆的周长,它等于圆锥侧面展开图扇形的弧长,而母线长为扇形的半径,然后根据扇形的面积公式计算即可.
解答:解:∵圆锥的底面圆的半径为1,
∴圆锥的底面圆的周长=2π×1=2π,
∴圆锥的侧面积=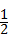 ×2π×2=2π.
×2π×2=2π.
故答案为:2π.
点评:本题考查了圆锥的侧面积公式:S=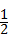 l•R.圆锥侧面展开图为扇形,底面圆的周长等于扇形的弧长,母线长为扇形的半径.
l•R.圆锥侧面展开图为扇形,底面圆的周长等于扇形的弧长,母线长为扇形的半径.
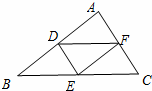
10、(2011•德州)如图,D,E,F分别为△ABC三边的中点,则图中平行四边形的个数为 3 .
考点:平行四边形的判定;三角形中位线定理。
专题:几何图形问题。
分析:根据三角形中位线的性质定理,可以推出DE∥AF,DF∥EC,DF∥BE且DE=AF,DF=EC,DF=BE,根据平行四边形的判定定理,即可推出有三个平行四边形.
解答:证明:∵D,E,F分别为△ABC三边的中点
∴DE∥AF,DF∥EC,DF∥BE且DE=AF,DF=EC,DF=BE
∴四边形ADEF、DECF、DFEB分别为平行四边形
故答案为3.
点评:本题主要考察平行四边的判定定理以及三角形中位线定理,关键在于找出相等而且平行的对边.
9、(2004•无锡)点(1,2)关于原点的对称点的坐标为 (﹣1,﹣2) .
考点:关于原点对称的点的坐标。
分析:由关于原点对称的点,横坐标与纵坐标都互为相反数可知:点(1,2)关于原点的对称点的坐标.
解答:解:因为关于原点对称的点,横坐标与纵坐标都互为相反数,
所以:点(1,2)关于原点的对称点的坐标为(﹣1,﹣2).
点评:解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com