
题目列表(包括答案和解析)
5.“恒盛”超市购进一批大米,大米的标准包装为每袋30kg,售货员任选6袋进行了称重检验,超过标准重量的记作“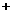 ”,
不足标准重量的记作“
”,
不足标准重量的记作“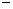 ”,他记
”,他记 录的结果是
录的结果是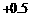 ,
,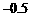 ,
,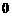 ,
,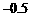 ,
,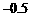 ,
,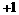 ,那么这6袋大米重量的平均数和极差分别是
,那么这6袋大米重量的平均数和极差分别是
A.0,1.5 B.29.5,1 C. 30,1.5 D.30.5,0
4.下列计算正确的是
A.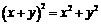 B.
B.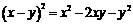 C.
C.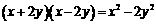 D.
D.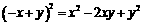
3.
 小华将一张如图1所示矩形纸片沿对角线剪开,他利用所得的两个直角三角形通过图形变换构成了下列四个图形,这四个图形中不是轴对称图形的是
小华将一张如图1所示矩形纸片沿对角线剪开,他利用所得的两个直角三角形通过图形变换构成了下列四个图形,这四个图形中不是轴对称图形的是



|
A B C D
2.二元一次方程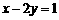 有无数多个解,下列四组值中不是该方程的解的是
有无数多个解,下列四组值中不是该方程的解的是
A.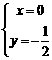 B.
B.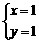 C.
C.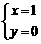 D.
D.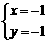
1.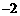 的相反数是
的相反数是
A.
2 B.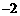 C.
C.
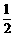 D.
D.
23、(2011•德州)在直角坐标系xoy中,已知点P是反比例函数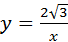 (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
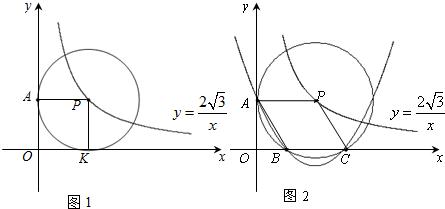
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的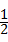 .若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
.若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
考点:二次函数综合题。
分析:(1)四边形OKPA是正方形.当⊙P分别与两坐标轴相切时,PA⊥y轴,PK⊥x轴,x轴⊥y轴,且PA=PK,可判断结论;
(2)①连接PB,设点P(x,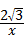 ),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=
),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=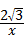 ,利用sin∠PBG=
,利用sin∠PBG=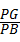 ,列方程求x即可;
,列方程求x即可;
②求直线PB的解析式,利用过A点或C点且平行于PB的直线解析式与抛物线解析式联立,列方程组求满足条件的M点坐标即可.
解答:(1)四边形OKPA是正方形.
证明:∵⊙P分别与两坐标轴相切,
∴PA⊥OA,PK⊥OK.
∴∠PAO=∠OKP=90°.
又∵∠AOK=90°,
∴∠PAO=∠OKP=∠AOK=90°.
∴四边形OKPA是矩形.
又∵OA=OK,
∴四边形OKPA是正方形.(2分)
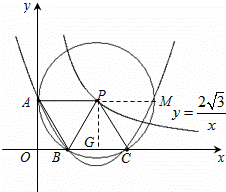 (2)①连接PB,设点P的横坐标为x,则其纵坐标为
(2)①连接PB,设点P的横坐标为x,则其纵坐标为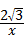 .
.
过点P作PG⊥BC于G.
∵四边形ABCP为菱形,
∴BC=PA=PB=PC.
∴△PBC为等边三角形.
在Rt△PBG中,∠PBG=60°,PB=PA=x,
PG=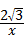 .
.
sin∠PBG=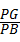 ,即
,即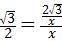 .
.
解之得:x=±2(负值舍去).
∴PG=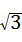 ,PA=BC=2.(4分)
,PA=BC=2.(4分)
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,
∴OB=OG﹣BG=1,OC=OG+GC=3.
∴A(0,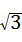 ),B(1,0)C(3,0).(6分)
),B(1,0)C(3,0).(6分)
设二次函数解析式为:y=ax2+bx+c.
据题意得:
解之得:a=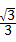 ,b=
,b=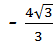 ,c=
,c=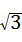 .
.
∴二次函数关系式为: .(9分)
.(9分)
②解法一:设直线BP的解析式为:y=ux+v,据题意得: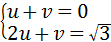
解之得:u=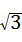 ,v=
,v=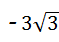 .
.
∴直线BP的解析式为: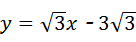 .
.
过点A作直线AM∥PB,则可得直线AM的解析式为: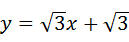 .
.
解方程组: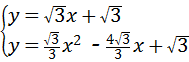
得: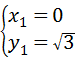 ;
;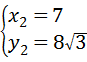 .
.
过点C作直线CM∥PB,则可设直线CM的解析式为: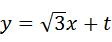 .
.
∴0=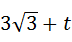 .
.
∴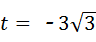 .
.
∴直线CM的解析式为: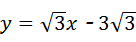 .
.
解方程组: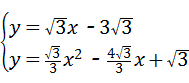
得: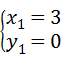 ;
;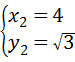 .
.
综上可知,满足条件的M的坐标有四个,
分别为:(0,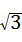 ),(3,0),(4,
),(3,0),(4,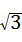 ),(7,
),(7,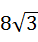 ).(12分)
).(12分)
解法二:∵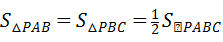 ,
,
∴A(0,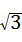 ),C(3,0)显然满足条件.
),C(3,0)显然满足条件.
延长AP交抛物线于点M,由抛物线与圆的轴对称性可知,PM=PA.
又∵AM∥BC,
∴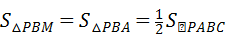 .
.
∴点M的纵坐标为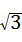 .
.
又点M的横坐标为AM=PA+PM=2+2=4.
∴点M(4,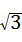 )符合要求.
)符合要求.
点(7,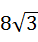 )的求法同解法一.
)的求法同解法一.
综上可知,满足条件的M的坐标有四个,
分别为:(0,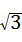 ),(3,0),(4,
),(3,0),(4,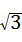 ),(7,
),(7,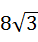 ).(12分)
).(12分)
解法三:延长AP交抛物线于点M,由抛物线与圆的轴对称性可知,PM=PA.
又∵AM∥BC,
∴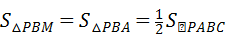 .
.
∴点M的纵坐标为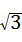 .
.
即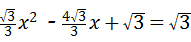 .
.
解得:x1=0(舍),x2=4.
∴点M的坐标为(4,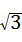 ).
).
点(7,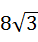 )的求法同解法一.
)的求法同解法一.
综上可知,满足条件的M的坐标有四个,
分别为:(0,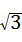 ),(3,0),(4,
),(3,0),(4,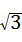 ),(7,
),(7,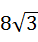 ).(12分)
).(12分)
点评:本题考查了二次函数的综合运用.关键是由菱形、圆的性质,形数结合解题.
22、(2011•德州)●观察计算
当a=5,b=3时,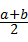 与
与 的大小关系是
的大小关系是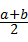 >
> .
.
当a=4,b=4时,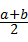 与
与 的大小关系是
的大小关系是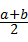 =
= .
.
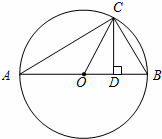 ●探究证明
●探究证明
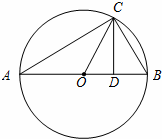
如图所示,△ABC为圆O的内接三角形,AB为直径,过C作CD⊥AB于D,设AD=a,BD=b.
(1)分别用a,b表示线段OC,CD;
(2)探求OC与CD表达式之间存在的关系(用含a,b的式子表示).
●归纳结论
根据上面的观察计算、探究证明,你能得出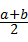 与
与 的大小关系是:
的大小关系是: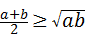 .
.
●实践应用
要制作面积为1平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
考点:相似三角形的判定与性质;几何不等式;圆周角定理。
分析:●观察计算:分别代入计算即可得出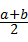 与
与 的大小关系;
的大小关系;
●探究证明:
(1)由于OC是直径AB的一半,则OC易得.通过证明△ACD∽△CBD,可求CD;
(2)分a=b,a≠b讨论可得出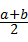 与
与 的大小关系;
的大小关系;
●实践应用:通过前面的结论长方形为正方形时,周长最小.
解答:解:●观察计算: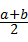 >
> ,
,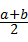 =
= .(2分)
.(2分)
●探究证明:
(1)∵AB=AD+BD=2OC,
∴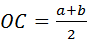 (3分)
(3分)
∵AB为⊙O直径,
∴∠ACB=90°.
∵∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD.
∴△ACD∽△CBD.(4分)
∴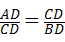 .
.
即CD2=AD•BD=ab,
∴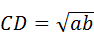 .(5分)
.(5分)
(2)当a=b时,OC=CD,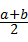 =
= ;
;
a≠b时,OC>CD,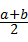 >
> .(6分)
.(6分)
●结论归纳: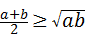 .(7分)
.(7分)
●实践应用
设长方形一边长为x米,则另一边长为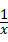 米,设镜框周长为l米,则
米,设镜框周长为l米,则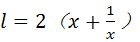 ≥
≥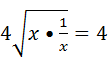 .(9分)
.(9分)
当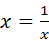 ,即x=1(米)时,镜框周长最小.
,即x=1(米)时,镜框周长最小.
此时四边形为正方形时,周长最小为4米.(10分)
点评:本题综合考查了几何不等式,相似三角形的判定与性质,通过计算和证明得出结论: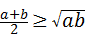 是解题的关键.
是解题的关键.
21、(2011•德州)为创建“国家卫生城市”,进一步优化市中心城区的环境,德州市政府拟对部分路段的人行道地砖、花池、排水管道等公用设施全面更新改造,根据市政建设的需要,须在60天内完成工程.现在甲、乙两个工程队有能力承包这个工程.经调查知道:乙队单独完成此项工程的时间比甲队单独完成多用25天,甲、乙两队合作完成工程需要30天,甲队每天的工程费用2500元,乙队每天的工程费用2000元.
(1)甲、乙两个工程队单独完成各需多少天?
(2)请你设计一种符合要求的施工方案,并求出所需的工程费用.
考点:分式方程的应用。
专题:工程问题。
分析:(1)如果设甲工程队单独完成该工程需x天,那么由“乙队单独完成此项工程的时间比甲队单独完成多用25天”,得出乙工程队单独完成该工程需(x+25)天.再根据“甲、乙两队合作完成工程需要30天”,可知等量关系为:甲工程队30天完成该工程的工作量+乙工程队30天完成该工程的工作量=1.
(2)首先根据(1)中的结果,排除在60天内不能单独完成该工程的乙工程队,从而可知符合要求的施工方案有两种:方案一:由甲工程队单独完成;方案二:由甲乙两队合作完成.针对每一种情况,分别计算出所需的工程费用.
解答:解:(1)设甲工程队单独完成该工程需x天,则乙工程队单独完成该工程需(x+25)天.(1分)
根据题意得: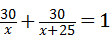 .(3分)
.(3分)
方程两边同乘以x(x+25),得30(x+25)+30x=x(x+25),
即x2﹣35x﹣750=0.
解之,得x1=50,x2=﹣15.(5分)
经检验,x1=50,x2=﹣15都是原方程的解.
但x2=﹣15不符合题意,应舍去.(6分)
∴当x=50时,x+25=75.
答:甲工程队单独完成该工程需50天,则乙工程队单独完成该工程需75天.(7分)
(2)此问题只要设计出符合条件的一种方案即可.
方案一:由甲工程队单独完成.(8分)
所需费用为:2500×50=125000(元).(10分)
方案二:由甲乙两队合作完成.
所需费用为:(2500+2000)×30=135000(元).(10分)
点评:本题考查分式方程在工程问题中的应用.分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.工程问题的基本关系式:工作总量=工作效率×工作时间.
20、(2011•德州)某兴趣小组用高为1.2米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α.测得A,B之间的距离为4米,tanα=1.6,tanβ=1.2,试求建筑物CD的高度.
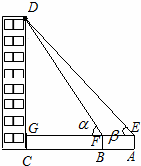
考点:解直角三角形的应用-仰角俯角问题。
专题:几何图形问题。
分析:CD与EF的延长线交于点G,设DG=x米.由三角函数的定义得到,在Rt△DGF中,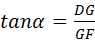 ,在Rt△DGE中,
,在Rt△DGE中,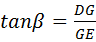 ,根据EF=EG﹣FG,得到关于x的方程,解出x,再加上1.2即为建筑物CD的高度.
,根据EF=EG﹣FG,得到关于x的方程,解出x,再加上1.2即为建筑物CD的高度.
解答:解:CD与EF的延长线交于点G,如图,设DG=x米.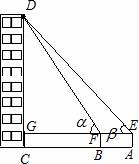
在Rt△DGF中,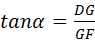 ,即
,即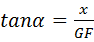 .
.
在Rt△DGE中,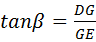 ,即
,即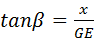 .
.
∴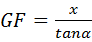 ,
,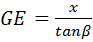 .
.
∴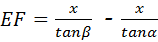 .
.
∴4=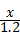 ﹣
﹣ ,
,
解方程得:x=19.2.
∴CD=DG+GC=19.2+1.2=20.4.
答:建筑物高为20.4米.
点评:本题考查了仰角的概念:向上看,视线与水平线的夹角叫仰角.也考查了测量建筑物高度的方法以及三角函数的定义.
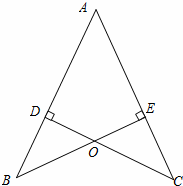
19、(2011•德州)如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
考点:全等三角形的判定与性质。
专题:应用题;证明题。
分析:(1)根据全等三角形的判定方法,证明△ACD≌△ABE,即可得出AD=AE,
(2)根据已知条件得出△ADO≌△AEO,得出∠DAO=∠EAO,即可判断出OA是∠BAC的平分线,即OA⊥BC.
解答:(1)证明:在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC,
∴△ACD≌△ABE,
∴AD=AE.
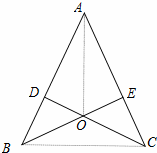 (2)互相垂直,
(2)互相垂直,
在Rt△ADO与△AEO中,
∵OA=OA,AD=AE,
∴△ADO≌△AEO,
∴∠DAO=∠EAO,
即OA是∠BAC的平分线,
又∵AB=AC,
∴OA⊥BC.
点评:本题考查了全等三角形的判定方法,以及全等三角形的对应边相等,对应角相等的性质,难度适中.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com