
题目列表(包括答案和解析)
6.对于反比例函数y = ,下列说法正确的是
A.图象经过点(1,-1) B.图象位于第二、四象限
C.图象是中心对称图形 D.当x<0时,y随x的增大而增大
[答案]C。
[考点]反比例函数。
[分析]根据反比例函数性质,直接得出结果。
5.若⊙O1、⊙O2的半径分别为4和6,圆心距O1O2=8,则⊙O1与⊙O2的位置关系是
A.内切 B.相交 C.外切 D.外离
[答案]B。
[考点]圆心距。
[分析] 。
。
4.已知a - b =1,则代数式2a -2b -3的值是
A.-1 B.1 C.-5 D.5
[答案]A。
[考点]代数式代换。
[分析]
3.下面四个几何体中,俯视图为四边形的是

[答案]D。
[考点]几何体的三视图。
[分析]根据几何体的三视图,直接得出结果。
2.下列运算正确的是
A.x2+ x3 = x5 B.x4·x2 = x6 C.x6÷x2 = x3 D.( x2 )3 = x8
[答案]B。
[考点]同底幂的乘法。
[分析]
1.-2的绝对值是
A.-2 B.- C.2 D.
[答案]C。
[考点]绝对值。
[分析]根据绝对值的定义,直接得出结果。
29、(2011•苏州)巳知二次函数y=a(x2﹣6x+8)(a>0)的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
(1)如图①.连接AC,将△OAC沿直线AC翻折,若点O的对应点0'恰好落在该抛物线的 对称轴上,求实数a的值;
(2)如图②,在正方形EFGH中,点E、F的坐标分别是(4,4)、(4,3),边HG位于边EF的 右侧.小林同学经过探索后发现了一个正确的命题:“若点P是边EH或边HG上的任意一点,则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等 (即这四条线段不能构成平行四边形).“若点P是边EF或边FG上的任意一点,刚才的结论是否也成立?请你积极探索,并写出探索过程;
(3)如图②,当点P在抛物线对称轴上时,设点P的纵坐标l是大于3的常数,试问:是否存在一个正数阿a,使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等 (即这四条线段能构成平行四边形)?请说明理由.

考点:二次函数综合题。
分析:(1)本题需先求出抛物线与x轴交点坐标和对称轴,再根据∠OAC=60°得出AO,从而求出a.
(2)本题需先分两种情况进行讨论,当P是EF上任意一点时,可得PC>PB,从而得出PB≠PA,PB≠PC,PB≠PD,即可求出线段PA、PB、PC、PD不能构成平行四边形.
(3)本题需先得出PA=PB,再由PC=PD,列出关于t与a的方程,从而得出a的值,即可求出答案.
解答:解:(1)令y=0,由a(x2﹣6x+8)=0,
解得x1=2,x2=4;
令x=0,解得y=8a,
∴点 A、B、C的坐标分别是(2,0)、(4,0)、(0,8a),
该抛物线对称轴为直线x=3,
∴OA=2,
如图①,设抛物线对称轴与x轴的交点为M,则AM=1,
由题意得:O′A=OA=2,
∴O′A=2AM,
∴∠O′AM=60°,
∴∠OAC=∠O′AC60°,
∴ ,AO=2
,AO=2 ,
,
即8a=2 ,
,
∴a= ;
;
(2)若点P是边EF或边FG上的任意一点,结论同样成立,
①如图②,设P是边EF上的任意一点(不与点E重合),连接PM,
∵点E(4,4)、F(4,3)与点B(4,0)在一直线上,点C在y轴上,
∴PB<4,PC≥4,
∴PC>PB,
又PD>PM>PB,PA>PM>PB,
∴PB≠PA,PB≠PC,PB≠PD,
∴此时线段PA、PB、PC、PD不能构成平行四边形,
②设P是边FG上的任意一点(不与点G重合),
∵点F的坐标是(4,3),点G的坐标是(5,3),
∴FG=3,GB= ,
,
∴3≤PB ,
,
∵PC≥4,
∴PC>PB,
又PD>PM>PB,PA>PM>PB,
∴PB≠PA,PB≠PC,PB≠PD,
∴此时线段PA、PB、PC、PD也不能构成平行四边形;
(3)存在一个正数a,使得线段PA、PB、PC、PD能构成一个平行四边形,
如图③,∵点A、B是抛物线与x轴交点,点P在抛物线对称轴上,
∴PA=PB,
∴当PC=PD时,线段PA、PB、PC、PD能构成一个平行四边形,
∵点C的坐标是(0,8a),点D的坐标是(3,﹣a),
点P的坐标是(3,t),
∴PC2=32+(t﹣8a)2,PD2=(t+a)2,
由PC=PD得PC2=PD2,
∴32+(t﹣8a)2=(t+a)2,
整理得:7a2﹣2ta+1=0有两个不相等的实数根a= =
= ,
,
显然a= 满足题意
满足题意
当t是一个大于3的常数时,存在一个正数a= ,使得线段PA、旁边、PC、PD能构成一个平行四边形.
,使得线段PA、旁边、PC、PD能构成一个平行四边形.



点评:本题主要考查了二次函数的综合问题,在解题时要注意运用数形结合和分类讨论,把二次函数的图象与性质和平行四边形的判定相结合是本题的关键.
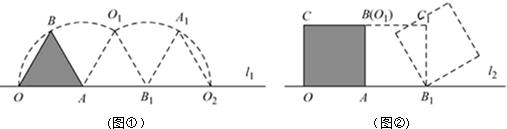
28、(2011•苏州)如图①,小慧同学把一个正三角形纸片(即△OAB)放在直线l1上.OA边与直线l1重合,然后将三角形纸片绕着顶点A按顺吋针方向旋转120°,此时点O运动到了点O1处,点B运动到了点B1处;小慧又将三角形纸片AO1B1,绕点B1按顺吋针方向旋转 120°,此时点A运动到了点A1处,点O1运动到了点O2处(即顶点O经过上述两次旋转到达O2处).
小慧还发现:三角形纸片在上述两次旋转的过程中.顶点O运动所形成的图形是两段圆弧,即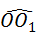 和
和 ,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形A001的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧与直线l1围成的图形面积等于扇形A001的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
小慧进行类比研究:如图②,她把边长为1的正方形纸片0ABC放在直线l2上,0A边与直线l2重合,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B2处,小慧又将正方形纸片 AO1C1B1绕顶点B1按顺时针方向旋转90°,….按上述方法经过若干次旋转后,她提出了如下问题:
问题①:若正方形纸片0ABC按上述方法经过3次旋转,求顶点0经过的路程,并求顶点O在此运动过程中所形成的图形与直线l2围成图形的面积;若正方形纸片OABC按上述方法经过5次旋转.求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点0经过的路程是 ?
?
考点:旋转的性质;等边三角形的性质;正方形的性质;弧长的计算;扇形面积的计算。
专题:几何图形问题。
分析:①根据正方形旋转3次和5次的路径,利用弧长计算公式以及扇形面积公式求出即可,
②再利用正方形纸片OABC经过4次旋转得出旋转路径,进而得出 =20(1+
=20(1+ )π+
)π+ ,即可得出旋转次数.
,即可得出旋转次数.
解答:解:①如图所示,正方形纸片OABC经过3次旋转,顶点O运动所形成的图形是三段圆弧,
∴顶点O在此过程中经过的路程为: 2+
2+ =(1+
=(1+ )π,
)π,
顶点O在此过程中经过的图形与直线l2围成的图形面积为:
 ×2+
×2+ +2×
+2× ×1=1+π.
×1=1+π.
正方形纸片OABC经过5次旋转,顶点O在此过程中经过的路程为:
 3+
3+ =(
=( +
+ )π,
)π,
②正方形纸片OABC经过4次旋转,顶点O在此过程中经过的路程为:
 2+
2+ =(1+
=(1+ )π,
)π,
∴ =20(1+
=20(1+ )π+
)π+ ,
,
∴正方形纸片OABC经过了81次旋转.

点评:此题主要考查了图形的旋转以及扇形面积公式和弧长计算公式,分别得出旋转3,4,5次旋转的路径是解决问题的关键.
27、(2011•苏州)已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.

(1)如图①,当PA的长度等于 2 时,∠PAD=60°;当PA的长度等于 2
时,∠PAD=60°;当PA的长度等于 2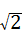 或
或 时,△PAD是等腰三角形;
时,△PAD是等腰三角形;
(2)如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3.设P点坐标为(a,b),试求2S1S3﹣S22的最大值,并求出此时a、b的值.
考点:相似三角形的判定与性质;二次函数的最值;正方形的性质;圆周角定理;解直角三角形。
专题:几何综合题;数形结合;方程思想。
分析:(1)由AB是直径,可得∠APB=90°,然后利用三角函数即可求得PA的长;当PA=PB时,△PAB是等腰三角形,然后由等腰三角形的性质与射影定理即可求得答案.
(2)过点P分别作PE⊥AB,PF⊥AD,垂足分别为E,F延长FP交BC于点G,则PG⊥BC,P点坐标为(a,b),PE=b,PF=a,PG=4﹣a,利用矩形的面积关系与二次函数的知识即可求得答案.
解答:解:(1)若∠PAD=60°,需∠PAB=30°,
∵AB是直径,
∴∠APB=90°,
∴PB=2,
则PA=2 ,
,
∴当PA的长度等于2 时,∠PAD=60°;
时,∠PAD=60°;
 若△PAD是等腰三角形,则只能是PA=PD,
若△PAD是等腰三角形,则只能是PA=PD,
过点P作PE⊥AD于E,作PM⊥AB于M,
则四边形EAMP是矩形,
∴PM=PE= AB=2,
AB=2,
∵PM2=AM•BM=4,
∵AM+BM=4,
∴AM=2,
∴PA=2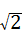 ,
,
同理可得P在P′时,PA=PB,
此时:PA= ;
;
∴当PA的长度等于2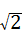 或
或 时,△PAD是等腰三角形;
时,△PAD是等腰三角形;
(2)过点P分别作PE⊥AB,PF⊥AD,垂足分别为E,F延长FP交BC于点G,
则PG⊥BC,
∵P点坐标为(a,b),
∴PE=b,PF=a,PG=4﹣a,
在△PAD,△PAB及△PBC中,
S1=2a,S2=2b,S3=8﹣2a,
∵AB为直径,
∴∠APB=90°,
∴PE2=AE•BE,
即b2=a(4﹣a),
∴2S1S3﹣S22=4a(8﹣2a)﹣4b2=﹣4b2+16a=﹣4(a﹣2)2+16,
∴当a=2时,b=2,2S1S3﹣S22有最大值16.

点评:此题考查了正方形的性质,圆周角的性质以及三角函数的性质等知识.此题综合性很强,解题时要注意数形结合与方程思想的应用.
26、(2011•苏州)如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点 (不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦长等于 2 (结果保留根号);
(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、C、0为顶点的三角形相似?请写出解答过程.

考点:圆周角定理;垂径定理;相似三角形的判定与性质;解直角三角形。
专题:几何综合题;数形结合。
分析:(1)过点O作OE⊥AB于E,由垂径定理即可求得AB的长;
(2)连接OA,由OA=OB,OA=OD,可得∠BAO=∠B,∠DAO=∠D,则可求得∠DAB的度数,又由圆周角等于同弧所对圆心角的一半,即可求得∠DOB的度数;
(3)由∠BCO=∠A+∠D,可得要使△DAC与△BOC相似,只能∠DCA=∠BCO=90°,然后由相似三角形的性质即可求得答案.
解答:解: 过点O作OE⊥AB于E,
过点O作OE⊥AB于E,
则AE=BE= AB,∠OEB=90°,
AB,∠OEB=90°,
∵OB=2,∠B=30°,
∴BE=OB•cos∠B=2× =
= ,
,
∴AB=2 ;
;
故答案为:2 ;
;
(2) 连接OA,
连接OA,
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D,
∴∠DAB=∠BAO+∠DAO=∠B+∠D,
又∵∠B=30°,∠D=20°,
∴∠DAB=50°,
∴∠BOD=2∠DAB=100°;
(3)∵∠BCO=∠A+∠D,
∴∠BCO>∠A,∠BCO>∠D,
∴要使△DAC与△BOC相似,只能∠DCA=∠BCO=90°,
此时∠BOC=60°,∠BOD=120°,
∴∠DAC=60°,
∴△DAC∽△BOC,
∵∠BCO=90°,
即OC⊥AB,
∴AC= AB=
AB= .
.
点评:此题考查了垂径定理,圆周角的性质以及相似三角形的判定与性质等知识.题目综合性较强,解题时要注意数形结合思想的应用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com