
题目列表(包括答案和解析)
18. (2011山东潍坊,20,9分)甲、乙两个盒子中装有质地、大小相同的小球,甲盒中有2个白球,1个黄球和1个蓝球;乙盒中有1个白球,2个黄球和若干个蓝球.从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍.
(1)求乙盒中蓝球的个数;
(2)从甲、乙两盒中分别任意摸取一球,求这两球均为蓝球的概率.
[解](1)设乙盒中有 个蓝球,则从乙盒中任意摸取一球,摸到蓝球的概率
个蓝球,则从乙盒中任意摸取一球,摸到蓝球的概率 ;
;
从甲盒中任意摸取一球,摸到蓝球的概率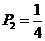 ;
;
根据题意,得 ,
,
解得 ,所以乙盒中有3个蓝球.
,所以乙盒中有3个蓝球.
(2)方法一:列表如下

由表格可以看出,可能的结果有24种,其中均为蓝球的有3种,因此从甲、乙两盒中各摸取一球,两球均为蓝球的概率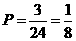 .
.
∴从甲、乙两盒中各摸取一球,两球均为蓝球的概率为 .
.
(也可以用画树状图法或枚举法)
方法二:从甲盒中任意摸取一球,摸到蓝球的概率为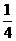 ,从乙盒中任意摸取一球,摸到蓝球的概率为
,从乙盒中任意摸取一球,摸到蓝球的概率为 .
.
则从甲、乙两盒中各摸取一球,两球均为蓝球的概率为 .
.
17. (2011江苏泰州,21,8分)一只不透明的袋子中装有2个白球和一个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,请用树状图或列表的方法列出所有可能的结果,写出两次摸出的球颜色相同的概率.
[答案]解:(1)树状图: 列表法:
|
2次 1次 |
红 |
白 |
白 |
|
红 |
(红,红) |
(红,白) |
(红,白) |
|
白 |
(白,红) |
(白,白) |
(白,白) |
|
白 |
(白,红) |
(白,白) |
(白,白) |


所有可能的结果如图所示,两次摸出的球颜色相同的概率为 .
.
16. (2011江苏宿迁,24,10分)在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
[答案]
解:(1)∵
|
|
1 |
2 |
3 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
|
3 |
(3,1) |
(3,2) |
(3,3) |
∴点M坐标的所有可能的结果有九个:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)、(3,3).
(2)P(点M在直线y=x上)=P(点M的横、纵坐标相等)= =
=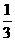 .
.
(3)∵
|
|
1 |
2 |
3 |
|
1 |
2 |
3 |
4 |
|
2 |
3 |
4 |
5 |
|
3 |
4 |
5 |
6 |
∴P(点M的横坐标与纵坐标之和是偶数)= .
.
15. (2011江苏苏州,24,6分)如图所示的方格地面上,标有编号1、2、3的3个小方格地面是空地,另外6个方格地面是草坪,除此以外小方格地面完全相同.
(1)一只自由飞行的小鸟,将随意落在图中所示的方格地面上,求小鸟落在草坪上的概率;
(2)现准备从图中所示的3个小方格空地中任选2个种植草坪,则编号为1、2的2个小方格空地种植草坪的概率是多少(用树状图或列表法求解)?

[答案]解:(1)P(小鸟落在草坪上)= =
= .
.
(2)用树状图或利用表格列出所有可能的结果:


所以编号为1、2的2个小方格空地种植草坪的概率为 =
=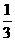 .
.
14. (2011江苏连云港,23,8分)一枚棋子放在边长为1个单位长度的正六边形ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位长度.棋子走到哪一点的可能性最大?求出棋子走到该点的概率.(用列表或画树状图的方法求解)

[答案]用列表法表示为

由上面的表格可知,两数和为4出现的次数最多,棋子走到E点的可能性最大,P(走到E点)= .
.
13. (2011湖南常德,20,6分)在一个不透明的口袋里,装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.若从中任意摸出一个球,这个球是白球的概率为0.5 .
(1)求口袋中红球的个数.
(2)若摸到红球记0分,摸到白球记1分,摸到黄球记2分,甲从口袋中摸出一个球不放回,再摸出一个.请用画树状图的方法求甲摸得到两个球且得2分的概率.
[答案](1)设袋中有红球x个,则有
 ,解得x=1.
,解得x=1.
所以,袋中的红球有1个.
(2)画树状图如下:


由上述树状图可知:所有可能出现的结果共有12种.其中摸出两个得2分的有4种.
所以 (从中摸出两个得2分)=
(从中摸出两个得2分)= .
.
12. (2011甘肃兰州,22,7分)如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字。现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y)。记S=x+y。
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)李刚为甲、乙两人设计了一个游戏:当S<6时甲获胜,否则乙获胜。你认为这个游戏公平吗?对谁有利?


[答案](1)1 (1,2) (1,4) (1,6)
2 (2,2) (2,4) (2,6)
3 (3,2) (3,4) (3,6)
4 (4,2) (4,4) (4,6)
 2
4
6
2
4
6
(2)甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 ,所以这个游戏不公平,对乙有利。
,所以这个游戏不公平,对乙有利。
11. (2011福建泉州,22,9分)在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在反比例函数 的图象上的概率;
的图象上的概率;
(3)求小明、小华各取一次小球所确定的数x、y满足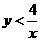 的概率.
的概率.
[答案]解:(1)
 x xy |
1 |
2 |
3 |
4 |
|
1 |
(1,1) |
(2,1) |
(3,1) |
(4,1) |
|
2 |
(1,2) |
(2,2) |
(3,2) |
(4,2) |
|
3 |
(1,3) |
(2,3) |
(3,3) |
(4,3) |
|
4 |
(1,4) |
(2,4) |
(3,4) |
(4,4) |
······························································································································································ 3分
(2)可能出现的结果共有16个,它们出现的可能性相等.·········································· 4分
满足点(x,y)落在反比例函数 的图象上(记为事件A)的结果有3个,即(1,4),(2,2),
的图象上(记为事件A)的结果有3个,即(1,4),(2,2),
(4,1),
所以P(A)= .·································································································································· 7分
.·································································································································· 7分
(3)能使x,y满足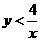 (记为事件B)的结果有5个,即(1,1),(1,2),(1,3),(2,1),(3,1),所以P(B)=
(记为事件B)的结果有5个,即(1,1),(1,2),(1,3),(2,1),(3,1),所以P(B)= 9分
9分
10.(2011江西,18,6分)甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛,
⑴请用树状图法或列表法,求恰好选中甲、乙两位同学的概率;
⑵若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率。
[答案](1)列表法如下:
|
|
甲 |
乙 |
丙 |
丁 |
|
甲 |
|
乙甲 |
丙甲 |
丁甲 |
|
乙 |
甲乙 |
|
丙乙 |
丁乙 |
|
丙 |
甲丙 |
乙丙 |
|
乙丙 |
|
丁 |
甲丙 |
乙丁 |
丙丁 |
|
所有可能出现的情况有12种,其中甲乙两位同学组合的情况有两种,
所以P(甲乙)= =
= .
.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,共有3种情况选中乙的情况有一种,所以P(恰好选中乙同学)= .
.
9. (2011四川重庆,23,10分)为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图:


(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
[答案](1)4÷20﹪=20(个);20-2-3-4-5-4=2(个),
(1×2+2×2+3×3+4×4+5×5+6×4)÷20=4(名).

答:该校平均每班有4名留守儿童.
(2)因为只有2名留守儿童的班级只有甲班和乙班两个,设甲班的2名留守儿童为a1,a2,乙班的2名留守儿童为b1,b2,列表如下:
|
|
a1 |
a2 |
b1 |
b2 |
|
a1 |
|
a1a2 |
a1b1 |
a1b2 |
|
a2 |
a1 a2 |
|
a2b1 |
a2b2 |
|
b1 |
a1 b1 |
a2 b1 |
|
b1b2 |
|
b2 |
a1 b2 |
a2 b2 |
b1 b2 |
|
由表格可知:共有12种情况,符合条件的有a1 a2、a1a2、b1 b2、b1b2四种,4÷12=.
答:所选两名留守儿童来自同一个班级的概率为.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com