
题目列表(包括答案和解析)
48.
47. (2011湖北宜昌,20,8分)如图,某商标是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
(1)求这个镶嵌图案中一个正三角形的面积;
(2)如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案申的正方形区域的概率为多少?(结果保留二位小数)

(第20题图)
[答案]解:(1)∵图案中正三角形的边长为2,∴高为 .(1分)∴正三角形的面积为
.(1分)∴正三角形的面积为 ×2×
×2× =
=  .(2分)(2)∵图中共有11个正方形, ∴图中正方形的面积和为11×(2×2)=44. (3分) ∵图中共有2个正六边形,∴图中正六边形的面积和为2×(6×
.(2分)(2)∵图中共有11个正方形, ∴图中正方形的面积和为11×(2×2)=44. (3分) ∵图中共有2个正六边形,∴图中正六边形的面积和为2×(6× ×2×
×2× )=12
)=12 .(4分)∵图中共有10个正三角形,∴图中正三角形的面积和为10
.(4分)∵图中共有10个正三角形,∴图中正三角形的面积和为10 .∵镶嵌图形的总面积为44+10
.∵镶嵌图形的总面积为44+10 +12
+12 =44+22
=44+22 (5分)≈81.4,∴点O落在镶嵌图案中正方形区域的概率为
(5分)≈81.4,∴点O落在镶嵌图案中正方形区域的概率为
 (7分)≈0.54.(8分)
(7分)≈0.54.(8分)
答:点O落在镶嵌图案中正方形区域的概率为0.54.(“≈”写为“=”不扣分)
46. (2011湖南湘潭市,22,6分)(本题满分6分)
九年级某班组织班团活动,班委会准备买一些奖品.班长王倩拿15元钱去商店全部用来购买钢笔和笔记本两种奖品,已知钢笔2元/支,笔记本1元/本,且每样东西至少买一件.
⑴ 有多少种购买方案?请列举所有可能的结果;
⑵ 从上述方案中任选一种方案购买,求买到的钢笔与笔记本数量相等的概率.
[答案]解:(1)设买钢笔x支,笔记本y本,则2x+y=15,所以y=15-2x。当x=1时,y=13;x=2时,y=11;x=3时,y=9;x=4时,y=7;x=5时,y=5;x=6时,y=3;x=7时,y=1;所以共有7种购买方案.
(2)在这7种方案中,买到的钢笔与笔记本数量相等的只有一种,所以P(买到的钢笔与笔记本数量相等)= .
.
45. (2011河北,21,8分)如图11,一转盘被等分成三个扇形,上面分别标有-1,1,2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形).
(1)若小静转动转盘一次,求得到负数的概率;
(2)小宇和小静分别转动转盘一次,若两人得到的数相同,则称两人“不谋而合”.用列表法(或画树状图)求两人“不谋而合”的概率.

[答案](1)P(得到负数)=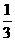
(2)列表:
|
|
-1 |
1 |
2 |
|
-1 |
(-1,-1) |
(-1,1) |
(-1,2) |
|
1 |
(1,-1) |
(1,1) |
(1,2) |
|
2 |
(2,-1) |
(2,1) |
(2,2) |
P(两人“不谋而合”)=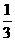
44. (2011贵州安顺,22,10分)有A、B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字-l,-2和-3.小强从A布袋中随机取出一个小球,记录其标有的数字为a,再从B布袋中随机取出一个小球,记录其标有的数字为b,这样就确定点Q的一个坐标为(a,b).
⑴用列表或画树状图的方法写出点Q的所有可能坐标;
⑵求点Q落在直线y=x-3上的概率.
[答案](1)列表或画树状图略,点Q的坐标有
(1,-1),(1,-2),(1,-3),(2,-1),(2,-2),(2,-3);
(2)“点Q落在直线y = x-3上”记为事件 ,所以
,所以 ,
,
即点Q落在直线y = x-3上的概率为 .
.
43. (2011广东湛江23,10分)一个口袋中有4个小球,这4个小球分别标记为1,2,3,4.
(1)随机模取一个小球,求恰好模到标号为2的小球的概率;
(2)随机模取一个小球然后放回,再随机模取一个小球,求两次模取的小球的标号的和为3的概率.
[答案](1)显然,随机模取一个小球,恰好模到标号为2的小球的概率为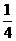 ;
;
(2)所以有可能的情况为:

而两次模取的小球的标号的和为3的情况有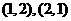 ,所以其概率为
,所以其概率为 .
.
42. (2011湖北鄂州,19,7分)有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
⑴先后两次抽得的数字分别记为s和t,则︱s-t︱≥1的概率.
⑵甲、乙两人做游戏,现有两种方案.A方案:若两次抽得相同花色则甲胜,否则乙胜.B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.
请问甲选择哪种方案胜率更高?
[答案]⑴ ⑵A方案P(甲胜)=
⑵A方案P(甲胜)= ,B方案P(甲胜)=
,B方案P(甲胜)= 故选择A方案甲的胜率更高.
故选择A方案甲的胜率更高.
41. (2011重庆市潼南,22,10分)端午节吃粽子是中华民族的传统习俗,一超市为了吸引消费者,增加销售量,
特此设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一
次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上则重转),当两
个转盘的指针所指字母都相同时,消费者就可以获得一次八折优惠价购买粽子的机会.
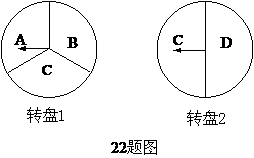
(1)用树状图或列表的方法(只选其中一种)表示出游戏可能出现的所有结果;
(2)若一名消费者只能参加一次游戏,则他能获得八折优惠价购买粽子的概率是多少?
[答案]解: (1)解法一:
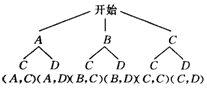
--------------4分
--------------6分
解法二:
 转盘2 转盘2转盘1 |
C |
D |
|
A |
(A,C) |
(A,D) |
|
B |
(B,C) |
(B,D) |
|
C |
(C,C) |
(C,D) |
(2)∵ 当两个转盘的指针所指字母都相同时的结果有一个,
∴P= -----------------------------10分
-----------------------------10分
40. (20011江苏镇江,21,8分)甲、乙、丙三个布袋都不透明,甲布袋中装有1个红球和1个白球;乙布袋中装有1个红球和2个白球;丙布袋中装有2个白球,这些球除颜色外都相同,从这匹个布袋中各随机地取出1个小球.
(1)取出的说个小球恰好是2个红球和1个白球概率是多少?
(2)取出的说个小球恰好全是白球的概率是多少?
[答案]
(1)从树状图可以看出,所有可能出现的结果共有12个,恰好是2个红球和1个白球的结果有2种,所以这个事件的概率是 ;
;
(2)3个球恰好全是白球的概率是 。
。
39. (2011江苏盐城,21,8分)小明有3支水笔,分别为红色、蓝色、黑色;有2块橡皮,分别为白色、灰色.小明从中任意取出1支水笔和1块橡皮配套使用.试用树状图或表格列出所有可能的结果,并求取出红色水笔和白色橡皮配套的概率.
[答案]解法一:画树状图:


P(红色水笔和白色橡皮配套)= .
解法二:用列表法:
|
白 |
灰 |
||||||
|
红 |
(红,白) |
(红,灰) |
||||||
|
蓝 |
(蓝,白) |
(蓝,灰) |
||||||
|
黑 |
(黑,白) |
(黑,灰) |
P(红色水笔和白色橡皮配套)= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com