
题目列表(包括答案和解析)
1. (2011山东滨州,7,3分)抛物线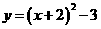 可以由抛物线
可以由抛物线 平移得到,则下列平移过程正确的是( )
平移得到,则下列平移过程正确的是( )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
[答案]B
[答案]D
28.解:(1)
理由如下:
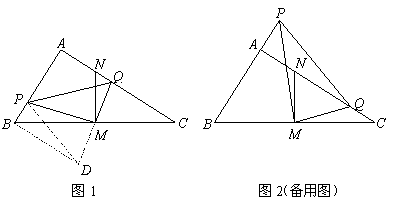
如图1,




 .
.






(2)
 cm.
cm.
又
 垂直平分
垂直平分 ,
, cm.
cm.

 =4cm.
=4cm.
①设 点的运动速度为
点的运动速度为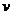 cm/s.
cm/s.
如图1,当 时,由(1)知
时,由(1)知
 即
即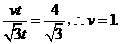
如图2,易知当 时,
时, .
.
综上所述, 点运动速度为1 cm/s.
点运动速度为1 cm/s.
②

 如图1,当
如图1,当 时,
时,


 .
.
如图2,当 时,
时, ,
, ,
,


 .
.
 综上所述,
综上所述,
(3) .
.
理由如下:
如图1,延长 至
至 ,使
,使 ,连结
,连结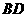 、
、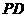 .
.

 、
、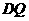 互相平分,
互相平分, 四边形
四边形 是平行四边形,
是平行四边形,
 .
.

 ,
,
 ,
,
 .
.

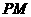 垂直平分
垂直平分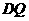 ,
,
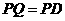 .
.
 .
.
27.解:(1)乙,甲,铁块的高度为14cm(或乙槽中水的深度达到14cm时刚好淹没铁块,说出大意即可)
(2)设线段 的函数关系式为
的函数关系式为 则
则


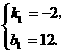
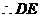 的函数关系式为
的函数关系式为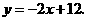
设线段 的函数关系式为
的函数关系式为 则
则
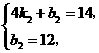



 的函数关系式为
的函数关系式为 .
.
由题意得 ,解得
,解得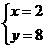 .
.
 注水2分钟时,甲、乙两水槽中水的深度相同.
注水2分钟时,甲、乙两水槽中水的深度相同.
(3) 水由甲槽匀速注入乙槽,
水由甲槽匀速注入乙槽, 乙槽前4分钟注入水的体积是后2分钟的2倍.
乙槽前4分钟注入水的体积是后2分钟的2倍.
设乙槽底面积与铁块底面积之差为S,则
 解得
解得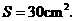
 铁块底面积为
铁块底面积为 .
.
 铁块的体积为
铁块的体积为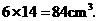
(4)甲槽底面积为
 铁块的体积为
铁块的体积为 ,
, 铁块底面积为
铁块底面积为 .
.
设甲槽底面积为 ,则注水的速度为
,则注水的速度为
由题意得 ,解得
,解得
 甲槽底面积为
甲槽底面积为
28.(本题满分12分)在 中,
中, 是
是 边的中点,
边的中点,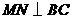 交
交 于点
于点 .动点
.动点 从点
从点 出发沿射线
出发沿射线 以每秒
以每秒 厘米的速度运动.同时,动点
厘米的速度运动.同时,动点 从点
从点 出发沿射线
出发沿射线 运动,且始终保持
运动,且始终保持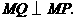 设运动时间为
设运动时间为 秒(
秒(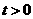 ).
).
(1)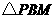 与
与 相似吗?以图1为例说明理由;
相似吗?以图1为例说明理由;
(2)若 厘米.
厘米.
①求动点 的运动速度;
的运动速度;
②设 的面积为
的面积为 (平方厘米),求
(平方厘米),求 与
与 的函数关系式;
的函数关系式;
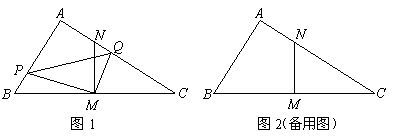
(3)探求 三者之间的数量关系,以图1为例说明理由.
三者之间的数量关系,以图1为例说明理由.
28.⑴假设第一次相切时,△ABC移至△A’B’C’处,A’C’与⊙O切于点E,连OE并延长,
交B’C’于F.设⊙O与直线l切于点D,连OD,则OE⊥A’C’,OD⊥直线l.
由切线长定理可知C’E= C’D,设C’D=x,则C’E= x,易知C’F=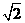 x
x
∴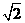 x+x=1 ∴x=
x+x=1 ∴x=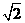 -1 ∴CC’=5-1-(
-1 ∴CC’=5-1-(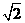 -1)=5-
-1)=5-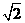 ………3分
………3分
∴点C运动的时间为 ………4分
………4分
∴点B运动的的距离为 ………5分
………5分
⑵∵△ABC与⊙O从开始运动到最后一次相切时,路程差为6,速度差为1
∴从开始运动到最后一次相切的时间为6秒…………7分
⑶∵△ABC与⊙O从开始运动到第二次相切时,路程差为4,速度差为1
∴从开始运动到第二次相切的时间为4秒, 此时△ABC移至△A”B”C”处,
A”B”=1+4× =3………10分
=3………10分
连接B”O并延长交A”C”于点P,易证B”P⊥A”C”,且OP=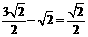 <1………9分
<1………9分
∴此时⊙O与A”C”相交

 ∴不存在.………12分
∴不存在.………12分
(扬州市2011年) 27.(本题满分12分)如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度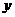 (厘米)与注水时间
(厘米)与注水时间 (分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(1)图2中折线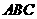 表示________槽中水的深度与注水时间的关系,线段
表示________槽中水的深度与注水时间的关系,线段 表示_______槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点
表示_______槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点 的纵坐标表示的实际意义是________________________________;
的纵坐标表示的实际意义是________________________________;
(2)注水多长时间时,甲、乙两个水槽中水的深度相同?
(3)若乙槽底面积为36平方厘米(壁厚不计),求乙槽中铁块的体积;
(4)若乙槽中铁块的体积为112立方厘米,求甲槽底面积(壁厚不计).(直接写出结果)

27.(1)y=2x-----1分;y=x2-----2分
(2)设解析式为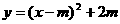 -----3分,
-----3分,
①则可得 -----5分,解得
-----5分,解得 (
( 舍去),
舍去),
所以 -----7分
-----7分
②S=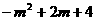 -----10分
-----10分
=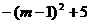
而
所以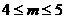 -----12分
-----12分
28.(本题满分12分)等腰直角△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.现△ABC以每秒2个单位的速度向右移动,同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大.
⑴ 当△ABC的边(BC边除外)与圆第一次相切时,点B移动了多少距离?
⑵ 若在△ABC移动的同时,⊙O也以每秒1个单位的速度向右移动,则△ABC从开始移动,到它的边与圆最后一次相切,一共经过了多少时间?
⑶ 在⑵的条件下,是否存在某一时刻,△ABC与⊙O的公共部分等于⊙O的面积?若存在,求出恰好符合条件时两个图形移动了多少时间?若不存在,请说明理由.

27.(本题满分12分)如图,Rt△AOB中,∠A=90°,以O为坐标原点建立直角坐标系,使点A在x轴正半轴上,OA=2,AB=8,点C为AB边的中点,抛物线的顶点是原点O,且经过C点.
(1)填空:直线OC的解析式为 ▲ ;
抛物线的解析式为 ▲ ;
(2) 现将该抛物线沿着线段OC移动,使其顶点M始终在线段OC上(包括端点O、C),抛物线与y轴的交点为D,与AB边的交点为E;
①是否存在这样的点D,使四边形BDOC为平行四边形?如存在,求出此时抛物线的解析式;如不存在,说明理由;
 ②设△BOE的面积为S,求S的取值范围.
②设△BOE的面积为S,求S的取值范围.
 |
|||
|
|||
25. 解析(by iC):第(1)问没什么好说的,送分。
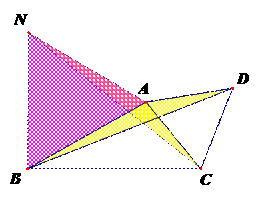 第(2)问,这个如果
第(2)问,这个如果 有这个条件的化,可以转化为共圆来做,可是此题并非如此。同样的如果按常规方法,如作高,求BD,题中条件基本用不上。
有这个条件的化,可以转化为共圆来做,可是此题并非如此。同样的如果按常规方法,如作高,求BD,题中条件基本用不上。
考虑题中的 ,在“外”的正
,在“外”的正 ,由(数学)图形的对称性,容易想到同里以AB,(BC边)向外也等边三角形,如图:正
,由(数学)图形的对称性,容易想到同里以AB,(BC边)向外也等边三角形,如图:正 ,
,
此时已经转化成极其常见的“经典基本图形”,连CN,
立即有:
对于第(2)问,反思一下条件,其实直接将 绕点A顺时针旋转
绕点A顺时针旋转 即可,想到旋转,就基本搞定了,你懂的。
即可,想到旋转,就基本搞定了,你懂的。

第(3)问:知道第(2)的思路与解法后,直接构造出2AH线段即可,如图:
 ,
,
显然有: ,
,
由三边对应相等,有两阴影三角形面积相等,
再倒倒角,知 成立。
成立。
2011年盐城市中考数学模拟试卷2011。6
25. 已知 ,以AC为边在
,以AC为边在 外作等腰
外作等腰 ,其中
,其中 。
。
(1)如图1,若 ,
,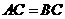 ,四边形ABCD是平行四边形,则
,四边形ABCD是平行四边形,则 ______;
______;
(2)如图2,若 ,
, 是等边三角形,
是等边三角形, ,
, 。求BD的长;
。求BD的长;
(3)如图3,若 为锐角,作
为锐角,作 于H。当
于H。当 时,
时, 是否成立?若不成立,请说明你的理由;若成立,证明你的结论。
是否成立?若不成立,请说明你的理由;若成立,证明你的结论。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com