
题目列表(包括答案和解析)
14. (2011江苏盐城,23,10分)已知二次函数y = - x2 - x + .
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y < 0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.

[答案](1)画图(如图);

(2)当y < 0时,x的取值范围是x<-3或x>1;
(3)平移后图象所对应的函数关系式为y=- (x-2)2+2(或写成y=- x2+2x).
13. (2011广东肇庆,25,10分)已知抛物线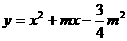 (
( >0)与
>0)与 轴交于
轴交于 、
、 两点.
两点.
(1)求证:抛物线的对称轴在 轴的左侧;
轴的左侧;
(2)若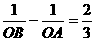 (
( 是坐标原点),求抛物线的解析式;
是坐标原点),求抛物线的解析式;
(3)设抛物线与 轴交于点
轴交于点 ,若D
,若D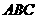 是直角三角形,求D
是直角三角形,求D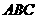 的面积.
的面积.
[答案](1)证明:∵ >0 ∴
>0 ∴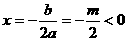
∴抛物线的对称轴在 轴的左侧
轴的左侧
(2)解:设抛物线与 轴交点坐标为A(
轴交点坐标为A( ,0),B(
,0),B( ,0),
,0),
则 ,
, , ∴
, ∴ 与
与 异号
异号
又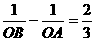
 ∴
∴ 由(1)知:抛物线的对称轴在
由(1)知:抛物线的对称轴在 轴的左侧
轴的左侧
∴ ,
, ∴
∴ ,
,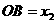
代入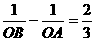 得:
得:
即 ,从而
,从而 ,解得:
,解得:
∴抛物线的解析式是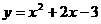
(3)[解法一]:当 时,
时, ∴抛物线与
∴抛物线与 轴交点坐标为
轴交点坐标为 (0,
(0, )
)
∵D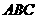 是直角三角形,且只能有AC⊥BC,又OC⊥AB,
是直角三角形,且只能有AC⊥BC,又OC⊥AB,
∴∠CAB= 90°- ∠ABC,∠BCO= 90°- ∠ABC,∴∠CAB =∠BCO
∴Rt△AOC∽Rt△COB,
∴ ,即
,即 ∴
∴
即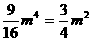 解得:
解得:
此时 =
= ,∴点
,∴点 的坐标为(0,-1)∴OC=1
的坐标为(0,-1)∴OC=1
又
∵ >0,∴
>0,∴ 即AB=
即AB= ∴D
∴D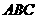 的面积=
的面积= ×AB×OC=
×AB×OC= ´
´ ´1=
´1=
[解法二]:略解: 当 时,
时, ∴点
∴点 (0,
(0, )
)
∵D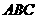 是直角三角形 ∴
是直角三角形 ∴
∴

∴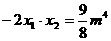 ∴
∴ 
解得: 
∴
12. (2011广东省,15,6分)已知抛物线 与x轴有交点.
与x轴有交点.
(1)求c的取值范围;
(2)试确定直线y=cx+l经过的象限,并说明理由.
[答案](1)∵抛物线与x轴没有交点
∴⊿<0,即1-2c<0
解得c>
(2)∵c>
∴直线y= x+1随x的增大而增大,
x+1随x的增大而增大,
∵b=1
∴直线y= x+1经过第一、二、三象限
x+1经过第一、二、三象限
11. (2011贵州贵阳,21,10分)
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;(3分)
(2)求点B的坐标;(3分)
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0),使S△ABD=S△ABC,求点D的坐标.(4分)

(第21题图)
[答案]解:(1)将(3,0)代入二次函数解析式,得
-32+2×3+m=0.
解得,m=3.
(2)二次函数解析式为y=-x2+2x+3,令y=0,得
-x2+2x+3=0.
解得x=3或x=-1.
∴点B的坐标为(-1,0).
(3)∵S△ABD=S△ABC,点D在第一象限,
∴点C、D关于二次函数对称轴对称.
∵由二次函数解析式可得其对称轴为x=1,点C的坐标为(0,3),
∴点D的坐标为(2,3).
10.(2011四川绵阳24,12)已知抛物线:y=x²-2x+m-1 与x轴只有一个交点,且与y轴交于A点,
如图,设它的顶点为B
(1)求m的值;
(2)过A作x轴的平行线,交抛物线于点C,求证是△ABC是等腰直角三角形;
(3)将此抛物线向下平移4个单位后,得到抛物线C',且与x 轴的左半轴交于E点,与y轴交于F点,如图.请在抛物线C'上求点P,使得△EFP是以EF为直角边的直角三角形.

[答案](1)抛物线与x轴只有一个交点,说明△=0,∴m=2
(2)∵抛物线的解析式是y=x²-2x+1,∴A(0,1),B(1,0)∴△AOB是等腰直角三角形,又AC∥OB,∴∠BAC=∠OAB=45°A,C是对称点,∴AB=BC,∴△ABC是等腰直角三角形。
(3)平移后解析式为y=x²-2x-3,可知E(-1,0),F(0,-3)∴EF的解析式为:y=-3x-3,平面内互相垂直的两条直线的k值相乘=-1,所以过E点或F点的直线为y=x+b把E点和F点分别代入可得b=或-3,∴y=x+或y=x-3列方程得解方程x1=-1,x2=, x1 是E点坐标舍去,把x2=代入得y=,∴P1(,)同理易得x1 = 0舍去,x2= 代入y=-,∴P2(,-)
6. (2011江苏南京,24,7分)(7分)已知函数y=mx2-6x+1(m是常数).
⑴求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
⑵若该函数的图象与x轴只有一个交点,求m的值.
[答案]解:⑴当x=0时, .
.
所以不论 为何值,函数
为何值,函数 的图象经过
的图象经过 轴上的一个定点(0,1).
轴上的一个定点(0,1).
⑵①当 时,函数
时,函数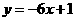 的图象与
的图象与 轴只有一个交点;
轴只有一个交点;
②当 时,若函数
时,若函数 的图象与
的图象与 轴只有一个交点,则方程
轴只有一个交点,则方程 有两个相等的实数根,所以
有两个相等的实数根,所以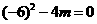 ,
,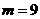 .
.
综上,若函数 的图象与
的图象与 轴只有一个交点,则
轴只有一个交点,则 的值为0或9.
的值为0或9.
5. (2011湖南怀化,22,10分)已知:关于x的方程
(1)
当a取何值时,二次函数 的对称轴是x=-2;
的对称轴是x=-2;
(2)
求证:a取任何实数时,方程 总有实数根.
总有实数根.
[答案]
(1)解:∵二次函数 的对称轴是x=-2
的对称轴是x=-2
∴
解得a=-1
经检验a=-1是原分式方程的解.
所以a=-1时,二次函数 的对称轴是x=-2;
的对称轴是x=-2;
(2)1)当a=0时,原方程变为-x-1=0,方程的解为x= -1;
2)当a≠0时,原方程为一元二次方程, ,
,
当 方程总有实数根,
方程总有实数根,
∴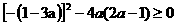
整理得,

∵a≠0时
 总成立
总成立
所以a取任何实数时,方程 总有实数根.
总有实数根.
4. (2011广东汕头,15,6分)已知抛物线 与x轴有交点.
与x轴有交点.
(1)求c的取值范围;
(2)试确定直线y=cx+l经过的象限,并说明理由.
[答案](1)∵抛物线与x轴没有交点
∴⊿<0,即1-2c<0
解得c>
(2)∵c>
∴直线y= x+1随x的增大而增大,
x+1随x的增大而增大,
∵b=1
∴直线y= x+1经过第一、二、三象限
x+1经过第一、二、三象限
3. (2011江苏泰州,27,12分)已知:二次函数y=x2+bx-3的图像经过点P(-2,5).
(1)求b的值,并写出当1<x≤3时y的取值范围;
(2)设点P1(m,y1)、P2(m+1,y2)、P3(m+2,y3)在这个二次函数的图像上.
①当m=4时,y1、y2、y3能否作为同一个三角形的三边的长?请说明理由;
②当m取不小于5的任意实数时,y1、y2、y3一定能作为同一个三角形三边的长,请说明理由.
[答案]解:(1)把点P代入二次函数解析式得5= (-2)2-2b-3,解得b=-2.
当1<x≤3时y的取值范围为-4<y≤0.
(2)①m=4时,y1、y2、y3的值分别为5、12、21,由于5+12<21,不能成为三角形的三边长.
②当m取不小于5的任意实数时,y1、y2、y3的值分别为m2-2m-3、m2-4、m2+2m-3,由于, m2-2m-3+m2-4>m2+2m-3,(m-2)2-8>0,
当m不小于5时成立,即y1+y2>y3成立.
所以当m取不小于5的任意实数时,y1、y2、y3一定能作为同一个三角形三边的长,
2. ( 2011重庆江津, 25,10分)已知双曲线 与抛物线y=zx2+bx+c交于A(2,3)、B(m,2)、c(-3,n)三点.
与抛物线y=zx2+bx+c交于A(2,3)、B(m,2)、c(-3,n)三点.
(1)求双曲线与抛物线的解析式;
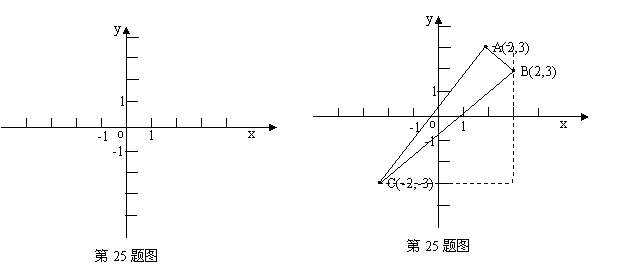
(2)在平面直角坐标系中描出点A、点B、点C,并求出△ABC的面积,
[答案](1)把点A(2,3)代入 得 :k=6·
得 :k=6·
∴反比例函数的解析式为: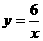 ·
·
把点B(m,2)、C(-3,n)分别代入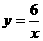 得: m=3,n=-2·
得: m=3,n=-2·
把A(2,3)、B(3,2)、C(-3,-2)分别代入y=ax2+bx+c得:
 解之得
解之得 
∴抛物线的解析式为:y=- ·
·
(2)描点画图
S△ABC= (1+6)×5-
(1+6)×5- ×1×1-
×1×1- ×6×4=
×6×4=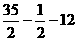 =5·
=5·
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com