
题目列表(包括答案和解析)
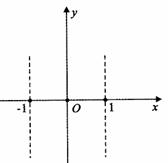
3. (2011江苏连云港,4,3分)关于反比例函数 的图象,下列说法正确的是( )
的图象,下列说法正确的是( )
A.必经过点(1,1) B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称 D.两个分支关于原点成中心对称
[答案]D
2.(2011湖南邵阳,5,3分)已知点(1,1)在反比例函数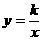 (k为常数,k≠0)的图像上,则这个反比例函数的大致图像是( )
(k为常数,k≠0)的图像上,则这个反比例函数的大致图像是( )




[答案]C提示:反比例函数过第一象限(也可由点(1,1)求得k=1),故选C。
1. (2011广东汕头,6,4分)已知反比例函数 的图象经过(1,-2).则
的图象经过(1,-2).则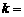 .
.
[答案]-2
21. (2011湖北宜昌,24,11分)已如抛物线y = ax2+bx+c 与直线y=m +n 相交于两点,这两点的坐标分别是(0,
+n 相交于两点,这两点的坐标分别是(0, )和(m-b,m2
– mb + n,其中a,b,c,m,n为实数,且a,m不为0.
)和(m-b,m2
– mb + n,其中a,b,c,m,n为实数,且a,m不为0.
(1)求c的值;
(2)设抛物线y
= ax2+bx+c与 轴的两个交点是(
轴的两个交点是( ,0)和(
,0)和( ,0),求
,0),求 的值;
的值;
(3)当 时,设抛物线y = ax2+bx+c与
时,设抛物线y = ax2+bx+c与 轴距离最大的点为P(
轴距离最大的点为P( ,
, ),求这时
),求这时 的最小值.
的最小值.
[答案]解:(1)∵(0, )在y=ax2+bx+c上,∴
)在y=ax2+bx+c上,∴  =a×02+b×0+c,∴ c=
=a×02+b×0+c,∴ c= .(1分)
(2)又可得 n=
.(1分)
(2)又可得 n= 。∵ 点(m-b,m2-mb+n)在y=ax2+bx+c上,∴ m2-mb
。∵ 点(m-b,m2-mb+n)在y=ax2+bx+c上,∴ m2-mb =a(m-b)2+b(m-b)
=a(m-b)2+b(m-b) ,∴(a-1)(m-b)2=0, (2分)若(m-b)=0,则(m-b, m2-mb+n)与(0,
,∴(a-1)(m-b)2=0, (2分)若(m-b)=0,则(m-b, m2-mb+n)与(0, )重合,与题意不合.∴ a=1.(3分,只要求出a=1,即评3分)
)重合,与题意不合.∴ a=1.(3分,只要求出a=1,即评3分)
∴抛物线y=ax2+bx+c,就是y=x2+bx .△=b2-4ac=b2-4×(
.△=b2-4ac=b2-4×( )>0,(没写出不扣分)∴抛物线y=ax2+bx+c与x轴的两个交点的横坐标就是关于x的二次方程0=ax2+bx+c的两个实数根,∴由根与系数的关系,得x1x2=
)>0,(没写出不扣分)∴抛物线y=ax2+bx+c与x轴的两个交点的横坐标就是关于x的二次方程0=ax2+bx+c的两个实数根,∴由根与系数的关系,得x1x2= .(4分)
(3)抛物线y=x2+bx
.(4分)
(3)抛物线y=x2+bx 的对称轴为x=
的对称轴为x= ,最小值为
,最小值为 .(没写出不扣分)设抛物线y=x2+bx
.(没写出不扣分)设抛物线y=x2+bx 在x轴上方与x轴距离最大的点的纵坐标为H,在x轴下方与x轴距离最大的点的纵坐标为h.
在x轴上方与x轴距离最大的点的纵坐标为H,在x轴下方与x轴距离最大的点的纵坐标为h.
① 当 <-1,即b>2时,在x轴上方与x轴距离最大的点是(1,yo),∴|H|=yo=
<-1,即b>2时,在x轴上方与x轴距离最大的点是(1,yo),∴|H|=yo= +b>
+b> , (5分),在x轴下方与x轴距离最大的点是(-1,yo),∴|h|=|yo|=|
, (5分),在x轴下方与x轴距离最大的点是(-1,yo),∴|h|=|yo|=| -b|=b-
-b|=b- >
> , (6分),∴|H|>|h|.∴这时|yo|的最小值大于
, (6分),∴|H|>|h|.∴这时|yo|的最小值大于 (7分)
(7分)
② 当-1≤ ≤0,即0≤b≤2时,在x轴上方与x轴距离最大的点是(1,yo),∴|H|=yo=
≤0,即0≤b≤2时,在x轴上方与x轴距离最大的点是(1,yo),∴|H|=yo= +b≥
+b≥ ,当b=0时等号成立.在x轴下方与x轴距离最大点的是 (
,当b=0时等号成立.在x轴下方与x轴距离最大点的是 ( ,
, ),∴|h|=|
),∴|h|=| |=
|=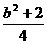 ≥
≥ ,当b=0时等号成立.∴这时|yo|的最小值等于
,当b=0时等号成立.∴这时|yo|的最小值等于 .(8分)
③ 当0<
.(8分)
③ 当0< ≤1,即-2≤b<0时,在x轴上方与x轴距离最大的点是(-1,yo),∴|H|=yo=1+(-1)b-
≤1,即-2≤b<0时,在x轴上方与x轴距离最大的点是(-1,yo),∴|H|=yo=1+(-1)b- =
= -b>
-b> ,在x轴下方与x轴距离最大的点是 (
,在x轴下方与x轴距离最大的点是 ( ,
, ),∴|h|=|yo|=|
),∴|h|=|yo|=| |=
|=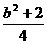 >12.
∴ 这 时 |yo|的 最 小 值 大 于
>12.
∴ 这 时 |yo|的 最 小 值 大 于 .(9分)
.(9分)
④ 当1< ,即b<-2时,在x轴上方与x轴距离最大的点是(-1,yo),
∴|H|=
,即b<-2时,在x轴上方与x轴距离最大的点是(-1,yo),
∴|H|= -b>
-b> ,在x轴下方与x轴距离最大的点是(1,yo),∴|h|=|
,在x轴下方与x轴距离最大的点是(1,yo),∴|h|=| +b|=-(b+
+b|=-(b+ )>
)> ,∴|H|>|h|,∴这时|yo|的最小值大于
,∴|H|>|h|,∴这时|yo|的最小值大于 (10分)
综上所述,当b=0,x0=0时,这时|yo|取最小值,为|yo|=
(10分)
综上所述,当b=0,x0=0时,这时|yo|取最小值,为|yo|= . (11分)
. (11分)
20.(2011湖北荆州,22,9分)(本题满分9分)如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴是,B(4,2),一次函数 的图象平分它的面积,关于x的函数
的图象平分它的面积,关于x的函数 的图象与坐标轴只有两个交点,求m的值.
的图象与坐标轴只有两个交点,求m的值.

第22题图
[答案] 解:过B作BE⊥AD于E,连结OB、CE交于 点P,
∵P为矩形OCBE的对称中心,则过P点的直线平分矩形OCBE的面积.
∵P为OB的中点,而B(4,2) ∴P点坐标为(2,1)
在Rt△ODC与Rt△EAB中,OC=BE,AB=CD
∴Rt△ODC≌Rt△EAB(HL),
∴S△ODC?=S△EBA?
∴过点(0,-1)与P(2,1)的直线即可平分等腰梯形面积,这条直线为y=kx-1
∴2k-1=1,∴k=1
又∵ 的图象与坐标轴只有两个交点,故
的图象与坐标轴只有两个交点,故
①当m=0时,y=-x+1,其图象与坐标轴有两个交点(0,1),(1,0)
②当m≠0时,函数 的图象为抛物线,且与y轴总有一个交点(0,2m+1)
的图象为抛物线,且与y轴总有一个交点(0,2m+1)
若抛物线过原点时,2m+1=0,即m= ,此时△=(3m+1)2-4m(2m+1)=
,此时△=(3m+1)2-4m(2m+1)=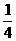 >0
>0
∴抛物线与x轴有两个交点且过原点,符合题意. 若抛物线不过原点,且与x轴只有一个交点,也合题意, 此时△′=(3m+1)2-4m(2m+1)=0
解之得:m1=m2=-1
综上所述,m的值为m=0或 或-1.
或-1.
19. (2011湖南湘潭市,25,10分)(本题满分10分)
如图,直线 交
交 轴于A点,交
轴于A点,交 轴于B点,过A、B两点的抛物线交
轴于B点,过A、B两点的抛物线交 轴于另一点C(3,0).
轴于另一点C(3,0).


⑴ 求抛物线的解析式;
⑵ 在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
[答案]解:(1)设抛物线的解析式为:y=ax2+bx+c。
∵直线 交
交 轴于A点,交
轴于A点,交 轴于B点,
轴于B点,
∴A点坐标为(-1,0)、B点坐标为(0,3).
又∵抛物线经过A、B、C三点,
∴ ,解得:
,解得: ,
,
∴抛物线的解析式为:y=-x2+2x+3.
(2)∵y=-x2+2x+3= 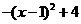 ,∴该抛物线的对称轴为x=1.
,∴该抛物线的对称轴为x=1.
设Q点坐标为(1,m),则 ,又
,又 .
.
当AB=AQ时,  ,解得:
,解得: ,
,
∴Q点坐标为(1, )或(1,
)或(1,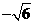 );
);
当AB=BQ时, ,解得:
,解得: ,
,
∴Q点坐标为(1,0)或(1,6);
当AQ=BQ时, ,解得:
,解得: ,
,
∴Q点坐标为(1,1).
∴抛物线的对称轴上是存在着点Q(1, )、(1,
)、(1,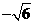 )、(1,0)、(1,6)、(1,1),使△ABQ是等腰三角形.
)、(1,0)、(1,6)、(1,1),使△ABQ是等腰三角形.
18. (2010湖北孝感,25,2分)如图(1),矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0.

(1)求点E、F的坐标(用含m的式子表示);(5分)
(2)连接OA,若△OAF是等腰三角形,求m的值;(4分)
(3)如图(2),设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值. (5分)
[答案]解:(1)∵四边形ABCD是矩形,
∴AD=BC=10,AB=CD=8,∠D=∠DCB=∠ABC=90°.
由折叠对称性:AF=AD=10,FE=DE.
在Rt△ABF中,BF=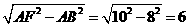 .
.
∴FC=4.
在Rt△ECF中,42+(8-x)2=x2,解得x=5.
∴CE=8-x=3.
∵B(m,0),∴E(m+10,3),F(m+6,0).

(2)分三种情形讨论:
若AO=AF,∵AB⊥OF,∴OB=BF=6.∴m=6.
若OF=AF,则m+6=10,解得m=4.
若AO=OF,在Rt△AOB中,AO2=OB2+AB2=m2+64,
∴(m+6)2= m2+64,解得m= .
.
综合得m=6或4或 .
.
(3)由(1)知A(m,8),E(m+10,3).
依题意,得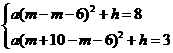 ,
,
解得
∴M(m+6,﹣1).
设对称轴交AD于G.
∴G(m+6,8),∴AG=6,GM=8-(﹣1)=9.
∵∠OAB+∠BAM=90°,∠BAM+∠MAG=90°,
∴∠OAB=∠MAG.
又∵∠ABO=∠MGA=90°,
∴△AOB∽△AMG.
∴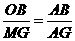 ,即
,即 .
.
∴m=12.
17. (2011贵州安顺,27,12分)如图,抛物线y= x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.


[答案](1)∵点A(-1,0)在抛物线y= x2 + bx-2上,∴
x2 + bx-2上,∴ × (-1 )2 + b× (-1) –2 = 0,解得b =
× (-1 )2 + b× (-1) –2 = 0,解得b =
∴抛物线的解析式为y= x2-
x2- x-2. y=
x-2. y= x2-
x2- x-2 =
x-2 = ( x2 -3x- 4 ) =
( x2 -3x- 4 ) = (x-
(x- )2-
)2-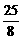 ,
,
∴顶点D的坐标为 ( , -
, -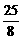 ).
).
(2)当x = 0时y = -2, ∴C(0,-2),OC = 2。
当y = 0时,  x2-
x2- x-2 = 0, ∴x1 = -1,
x2 = 4, ∴B (4,0)
x-2 = 0, ∴x1 = -1,
x2 = 4, ∴B (4,0)
∴OA = 1, OB = 4, AB = 5.
∵AB2 = 25, AC2 = OA2 + OC2 = 5, BC2 = OC2 + OB2 = 20,
∴AC2 +BC2 = AB2. ∴△ABC是直角三角形.
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC + MD的值最小。

解法一:设抛物线的对称轴交x轴于点E.
∵ED∥y轴, ∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴
∴ ,∴m =
,∴m = .
.
解法二:设直线C′D的解析式为y = kx + n ,
则 ,解得n =
2,
,解得n =
2,  .
.
∴ .
.
∴当y = 0时, 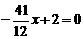 ,
,
 . ∴
. ∴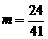 .
.
16. (2011广东中山,15,6分)已知抛物线 与x轴有两个不同的交点.
与x轴有两个不同的交点.
(1)求c的取值范围;
(2)抛物线 与x轴两交点的距离为2,求c的值.
与x轴两交点的距离为2,求c的值.
[解](1)∵抛物线与x轴有两个不同的交点
∴⊿>0,即1-2c>0
解得c<
(2)设抛物线 与x轴的两交点的横坐标为
与x轴的两交点的横坐标为 ,
,
∵两交点间的距离为2,
∴ ,
,
由题意,得
解得
∴c=
即c的值为0.
15. (20011江苏镇江,24,7分)如图,在△ABO中,已知点A( ,3),B(-1,-1),O(0,0),正比例y=-x的图象是直线l,直线AC∥x轴交直线l于点C.
,3),B(-1,-1),O(0,0),正比例y=-x的图象是直线l,直线AC∥x轴交直线l于点C.
(1)C点坐标为_____;
(2)以点O为旋转中心,将△ABO顺时针旋转角a(0°<a<180°),使得点B落在直线l上的对应点为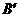 ,点A的对应点为
,点A的对应点为 ,得到△
,得到△ .
.
①∠a=_____;
②画出△ ;
;
(3)写出所有满足△DOC∽△AOB的点D的坐标.

[答案]解:(1)C点坐标为(-3,3);(2)①∠α=90°②略 (3)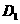 (9,-
(9,- ),
),  (
( ,-9).
,-9).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com