
题目列表(包括答案和解析)
10.(2011四川重庆,22,10分)如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE=.
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE=.
(1)求该反比例函数和一次函数;
(2)求△AOC的面积.

[答案](1)过A点作AD⊥x轴于点D,∵sin∠AOE= ,OA=5,
∴在Rt△ADO中,∵sin∠AOE= == ,
∴AD=4,DO==3,又点A在第二象限∴点A的坐标为(-3,4),
将A的坐标为(-3,4)代入y= ,得4=∴m=-12,∴该反比例函数的解析式为y=-,
∵点B在反比例函数y=-的图象上,∴n=-=-2,点B的坐标为(6,-2),∵一次函数y=kx+b(k≠0)的图象过A、B两点,
∴,∴
∴该一次函数解析式为y=-x+2.
(2)在y=-x+2中,令y=0,即-x+2=0,∴x=3,
∴点C的坐标是(3,0),∴OC=3, 又DA=4,
∴S△AOC=×OC×AD=×3×4=6,所以△AOC的面积为6.
9. (2011浙江义乌,22,10分)如图,在直角坐标系中,O为坐标原点. 已知反比例函数
(2011浙江义乌,22,10分)如图,在直角坐标系中,O为坐标原点. 已知反比例函数
y= (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为 .
 (1)求k和m的值;
(1)求k和m的值;
(2)点C(x,y)在反比例函数y= 的图象上,求当 1≤x≤3时函数值y的取值范围;
1≤x≤3时函数值y的取值范围;
(3)过原点O的直线l与反比例函数y= 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.

[答案](1)∵A(2,m) ∴OB=2 AB=m
∴S△AOB= •OB•AB=
•OB•AB= ×2×m=
×2×m= ∴m=
∴m=
∴点A的坐标为(2, ) 把A(2,
) 把A(2, )代入y=
)代入y= ,得
,得 =
=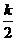
∴k=1
(2)∵当x=1时,y=1;当x=3时,y=
又 ∵反比例函数y= 在x>0时,y随x的增大而减小,
在x>0时,y随x的增大而减小,
∴当1≤x≤3时,y的取值范围为 ≤y≤1。
≤y≤1。
(3) 由图象可得,线段PQ长度的最小值为2 。
。
8. (2011浙江省,18,8分)若反比例函数 与一次函数
与一次函数 的图象都经过点A(a,2)
的图象都经过点A(a,2)
(1)求反比例函数 的解析式;
的解析式;
(2) 当反比例函数 的值大于一次函数
的值大于一次函数 的值时,求自变量x的取值范围.
的值时,求自变量x的取值范围.

[答案](1)∵  的图象过点A(a,2) ∴ a=3
的图象过点A(a,2) ∴ a=3
∵  过点A(3,2)
∴ k=6 ∴
过点A(3,2)
∴ k=6 ∴
(2) 求反比例函数 与一次函数
与一次函数 的图象的交点坐标,得到方程:
的图象的交点坐标,得到方程:
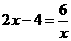 解得:x1= 3 , x2= -1
解得:x1= 3 , x2= -1
∴ 另外一个交点是(-1,-6)
∴ 当x<-1或0<x<3时,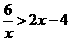
7. (2011山东烟台,22,8分)如图,已知反比例函数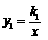 (k1>0)与一次函数
(k1>0)与一次函数 相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2 .
相交于A、B两点,AC⊥x轴于点C.若△OAC的面积为1,且tan∠AOC=2 .
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?

[答案]解(1)在Rt△OAC中,设OC=m.
∵tan∠AOC= =2,
=2,
∴AC=2×OC=2m.
∵S△OAC= ×OC×AC=
×OC×AC= ×m×2m=1,
×m×2m=1,
∴m2=1
∴m=1(负值舍去).
∴A点的坐标为(1,2).
把A点的坐标代入 中,得
中,得
k1=2.
∴反比例函数的表达式为 .
.
把A点的坐标代入 中,得
中,得
k2+1=2,
∴k2=1.
∴一次函数的表达式 .
.
(2)B点的坐标为(-2,-1).
当0<x<1和x<-2时,y1>y2.
6. (2011山东泰安,26 ,10分)如图,一次函数y=k1x+b的图象经过A(0,-2),B(1,0)两点,与反比例函数y=的图象在第一象限内的交点为M,若△OBM的面积为2。
(1)求一次函数和反比全例函数的表达式。
(2)在x轴上存在点P,使AM⊥PM?若存在,求出点P的坐标,若不存在,说明理由。

[答案](1)∵直线y=k1x+b过A(0,-2),B(1,0)
∴ ∴
∴一次函数的表达式为y=2x-2
设M(m,n),作MD⊥x轴于点D
∵S△OBM=2
∴OB·MD=2 ∴n=2
∴n=4
将M(m,4)代入y=2x-2得:4=2m-2 ∴m=3
∵4= ∴k2=12
所以反比例函数的表达式为y=
(2)过点M(3,4)作MP⊥AM交x轴于点P
∵MD⊥BP ∴∠PMD=∠MBD=∠ABO
∴tan∠PMD= tan∠MBD= tan∠ABO===2
∴在Rt△PDM中,=2 ∴PD=2MD=8
∴PO=OD+PD=11
∴在x轴上存在点P,使PM⊥AM,此时点P的坐标为(11,0)
5. (2011山东济宁,20,7分)如图,正比例函数 的图象与反比例函数
的图象与反比例函数
 在第一象限的图象交于
在第一象限的图象交于 点,过
点,过 点作
点作 轴的垂线,垂足为
轴的垂线,垂足为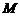 ,已知
,已知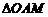 的面积为1.
的面积为1.
(1)求反比例函数的解析式;
(2)如果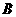 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点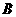 与点
与点 不重合),且
不重合),且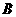 点的横坐标为1,在
点的横坐标为1,在 轴上求一点
轴上求一点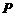 ,使
,使 最小.
最小. 

[答案](1) 设 点的坐标为(
点的坐标为( ,
, ),则
),则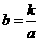 .∴
.∴ .
.
∵ ,∴
,∴ .∴
.∴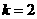 .
.
∴反比例函数的解析式为 .··············· 3分
.··············· 3分
(2) 由 得
得 ∴
∴ 为(
为( ,
,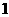 ). ·········· 4分
). ·········· 4分
设 点关于
点关于 轴的对称点为
轴的对称点为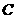 ,则
,则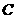 点的坐标为(
点的坐标为( ,
,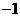 ).
).
令直线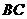 的解析式为
的解析式为 .
.
∵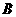 为(
为(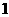 ,
, )∴
)∴ ∴
∴
∴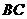 的解析式为
的解析式为 .················· 6分
.················· 6分
当 时,
时, .∴
.∴ 点为(
点为( ,
, ).…………………………7分
).…………………………7分
4. (2011山东菏泽,17(1),7分)已知一次函数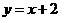 与反比例函数
与反比例函数 ,其中一次函数
,其中一次函数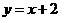 的图象经过点P(
的图象经过点P(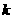 ,5).
,5).
①试确定反比例函数的表达式;
②若点Q是上述一次函数与反比例函数图象在第三象限的交点,求点Q的坐标
[答案]解:因一次函数y=x+2的图象经过点P(k,5),
所以得5=k+2,解得k=3
所以反比例函数的表达式为
(2)联立得方程组
解得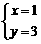 或
或
故第三象限的交点Q的坐标为(-3,-1)
3. (2011广东广州市,23,12分)
已知Rt△ABC的斜边AB在平面直角坐标系的x轴上,点C(1,3)在反比例函数y = 的图象上,且sin∠BAC= .
(1)求k的值和边AC的长;
(2)求点B的坐标.
[答案](1)把C(1,3)代入y = 得k=3
设斜边AB上的高为CD,则
sin∠BAC==
∵C(1,3)
∴CD=3,∴AC=5
(2)分两种情况,当点B在点A右侧时,如图1有:
AD==4,AO=4-1=3
∵△ACD∽ABC
∴AC2=AD·AB
∴AB==
∴OB=AB-AO=-3=
此时B点坐标为(,0)




图1 图2
当点B在点A左侧时,如图2
此时AO=4+1=5
OB= AB-AO=-5=
此时B点坐标为(-,0)
所以点B的坐标为(,0)或(-,0).
2. (2011安徽,21,12分)如图,函数 的图象与函数
的图象与函数 (
( )的图象交于A、B两点,与
)的图象交于A、B两点,与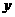 轴交于C点,已知A点坐标为(2,1),C点坐标为(0,3).
轴交于C点,已知A点坐标为(2,1),C点坐标为(0,3).
(1)求函数 的表达式和B点的坐标;
的表达式和B点的坐标;
(2)观察图象,比较当 时,
时, 与
与 的大小.
的大小.


[答案](1)由题意,得 解得
解得 ∴
∴ 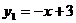 ;
;
又A点在函数 上,所以
上,所以 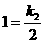 ,解得
,解得 , 所以
, 所以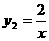 ;
;
解方程组 得
得 ,
,  .
.
所以点B的坐标为(1, 2).
(2)当x=1或x=2时,y1=y2;
当1<x<2时,y1>y2;
当0<x<1或x>2时,y1<y2.
1. (2011浙江省舟山,19,6分)如图,已知直线 经过点P(
经过点P( ,
, ),点P关于
),点P关于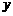 轴的对称点P′在反比例函数
轴的对称点P′在反比例函数 (
(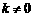 )的图象上.
)的图象上.
(1)求 的值;
的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.


[答案](1)将P(-2,a)代入 得a=-2×(-2)=4;
得a=-2×(-2)=4;
(2) P′(2,4)
(3)将P′(2,4)代入 得4=
得4=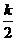 ,解得k=8,∴反比例函数的解析式为
,解得k=8,∴反比例函数的解析式为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com