
题目列表(包括答案和解析)
23. (2010湖北孝感,24,10分)健身运动已成为时尚,某公司计划组装A、B两种型号的健身器材共40套,捐赠给社区健身中心.组装一套A型健身器材需甲种部件7个和乙种部件4个,组装一套B型健身器材需甲种部件3个和乙种部件6个.公司现有甲种部件240个,乙种部件196个.
(1)公司在组装A、B两种型号的健身器材时,共有多少种组装方案;(5分)
(2)组装一套A型健身器材需费用20元,组装一套B型健身器材需费用18元.求总组装费用最少的组装方案,最少组装费用是多少?(5分)
[答案]解:(1)设该公司组装A型器材x套,则组装B型器材(40-x)套,依题意,得

解得22≤x≤30.
由于x为整数,∴x取22,23,24,25,26,27,28,29,30.
∴组装A、B两种型号的健身器材共有9种组装方案.
(2)总的组装费用y=20x+18(40-x)=2x+720.
∵k=2>0,∴y随x的增大而增大.
∴当x=22时,总的组装费用最少,最少组装费用是2×22+720=764元.
总组装费用最少的组装方案:组装A型器材22套,组装B型器材18套.
22. (2011河北,24,9分)已知A,B两地的路程为240千米.某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预定.
现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图13-1)、上周货运量折现统计图(如图13-2)等信息如下:
货运收费项目及收费标准表
|
运输工具 |
运输费单价 元/(吨·时) |
冷藏费单价 元/(吨·时) |
固定费用 元/次 |
|
汽车 |
2 |
5 |
200 |
|
火车 |
1.6 |
5 |
2280 |


(1)汽车的速度为 千米/时,
火车的速度为 千米/时;
(2)设每天用汽车和火车运输的总费用分别为y汽(元)和y火(元),分别求y汽、和y火与x的函数关系式(不必写出x的取值范围),及x为何值时y汽>和y火;
(总费用=运输费+冷藏费+固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输总费用较省?
[答案](1)60,100
(2)依题意,得
 =500x+200
=500x+200

 =396x+2280
=396x+2280
若 >
> ,则500x+200>396x+2280,所以x>20
,则500x+200>396x+2280,所以x>20
(3)上周运货量平均数为(17+20+19+22+22+23+24)÷7=21>20,
从平均数分析,建议预定火车费用较省;
从折线图走势分析,上周运货量周四(含周四)后大于20且呈上升趋势,建议预定火车费用较省
21. (2011湖北襄阳,24,10分)
为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为 (元),节假日购票款为
(元),节假日购票款为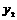 (元).
(元). ,
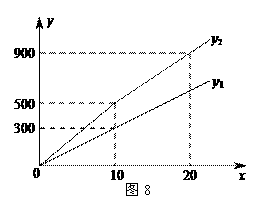
,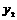 与x之间的函数图象如图8所示.
与x之间的函数图象如图8所示.
(1)观察图象可知:a= ;b= ;m= ;
(2)直接写出 ,
,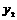 与x之间的函数关系式;
与x之间的函数关系式;
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A,B两个团队合计50人,求A,B两个团队各有多少人?

[答案]
(1) (填对一个记1分)················································ 3分
(填对一个记1分)················································ 3分
(2) ;······················································································································ 4分
;······················································································································ 4分
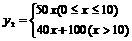 .································································································ 6分
.································································································ 6分
(3)设A团有n人,则B团有(50-n)人.
当0≤n≤10时,
解之,得n=20,这与n≤10矛盾.··································································· 7分
当n>10时, ·························································· 8分
·························································· 8分
解之,得,n=30,··································································································· 9分
∴50-30=20
答:A团有30人,B团有20人. 10分
20.(2011广东茂名,21,8分)某学校要印制一批《学生手册》,甲印刷厂提出:每本收1元印刷费,另收500元制版费;乙印刷厂提出:每本收2元印刷费,不收制版费.
(1)分别写出甲、乙两厂的收费 (元) 、
(元) 、 (元)与印制数量
(元)与印制数量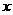 (本)之间的关系式; (4分)
(本)之间的关系式; (4分)
(2)问:该学校选择哪间印刷厂印制《学生手册》比较合算?请说明理由. (4分)
[答案]解:(1) ,
, .
.
(2)当 >
> 时,
时, 即
即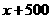 >
> ,则
,则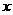 <500 ,
<500 ,
当 =
= 时,
时,  即
即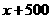 =
= ,则
,则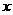 =500,·
=500,·
当 <
< 时,
时, 即
即 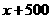 <
< , 则
, 则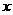 >500,
>500,
∴该学校印制学生手册数量小于500本时应选择乙厂合算,当印制学生手册数量大于500本时应选择甲厂合算,当印制学生手册数量等于500本时选择两厂费用都一样 .
19. (2011贵州贵阳,23,10分)
童星玩具厂工人的工作时间为:每月22天,每天8小时.工资待遇为:按件计酬,多劳多得,每月另加福利工资500元,按月结算.该厂生产A、B两种产品,工人每生产一件A种产品可得报酬1.50元,每生产一件B产品可得报酬2.80元.该厂工人可以选择A、B两种产品中的一种或两种进行生产.工人小李生产1件A产品和1件B产品需35分钟;生产3件A产品和2件B产品需85分钟.
(1)小李生产1件A产品需要______分钟,生产1件B产品需要______分钟.(4分)
(2)求小李每月的工资收入范围.(6分)
[答案]解:(1)设小李生产1件A产品需要m分钟,生产1件B产品需要n分钟,则
,解得,.
(2)设小李每月生产A产品x件,则生产B产品的件数为,设小李每月的工资为y元,则
y=1.50x+2.80×+500.
整理,得
y=-0.6x+1987.40.
∵≥0,
∴x≤704,
∴x的取值范围为0≤x≤704.
当x=0时,y取最大值1987.40;当x=704时,y取最小值1565.00.
∴小李每月的工资收入范围为1565.00~1987.40元.
18. (2011四川乐山21,10分)某学校的复印任务原来由甲复印社承接,其收费y(元)与复印页数x(页)的关系如下表:
|
x(页) |
100 |
200 |
400 |
1000 |
… |
|
y(元) |
40 |
80 |
160 |
400 |
|
⑴、若y与x满足初中学过的某一函数关系,求函数的解析式;
⑵、现在乙复印社表示:若学校先按每月付给200元的承包费,则可按每页0.15元收费。则乙复印社每月收费y(元)与复印页数x(页)的函数关系为 ;
⑶、在给出的坐标系内画出(1)、(2)中的函数图象,并回答每月复印页数在1200左右应选择哪个复印社?

[答案]
解:⑴.
⑵。
⑶.

由图像可知,当每月复印页数在1200左右,应选择乙复印社更合算。
17. (2011江苏南京,22,7分)小颖和小亮上山游玩,小颖乘会缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min才乘上缆车,缆车的平均速度为180 m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
⑴小亮行走的总路程是____________㎝,他途中休息了________min.
⑵①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?


[答案]解:⑴3600,20.
⑵①当 时,设y与x的函数关系式为
时,设y与x的函数关系式为 .
.
根据题意,当 时,
时, ;当
;当 ,
, .
.
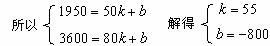
 所以,
所以,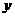 与
与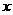 的函数关系式为
的函数关系式为 .
.
②缆车到山顶的路线长为3600÷2=1800( ),
),
缆车到达终点所需时间为1800÷180=10( ).
).
小颖到达缆车终点时,小亮行走的时间为10+50=60( ).
).
把 代入
代入 ,得y=55×60-800=2500.
,得y=55×60-800=2500.
所以,当小颖到达缆车终点时,小亮离缆车终点的路程是3600-2500=1100( ).
).
16. (2011江苏淮安,27,2分)小华观察钟面(题27-1图),了解到钟面上的分针每小时旋转360度,时针每小时旋转30度.他为了进一步研究钟面上分针与时针的旋转规律,从下午2:00开始对钟面进行了一个小时的观察.为了研究方便,他将分针与时针原始位置OP(题27-2图)的夹角记为y1度,时针与原始位置OP的夹角记为y2度(夹角是指不大于平角的角),旋转时间记为t分钟,观察结束后,他利用所得的数据绘制成图象(题27-3图),并求出了y1与t的函数关系式: .
.



请你完成:
(1)求出题27-3图中y2与t的函数关系式;
(2)直接写出A、B两点的坐标,并解释这两点的实际意义;
(3)若小华继续观察一小时,请你在题27-3图中补全图象.
[答案]解:(1)由题27-3图可知:y2的图象经过点(0,60)和(60,90),设y2=at+b,则
 ,
,
解得 .
.
∴题27-3图中y2与t的函数关系式为:y2=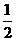 t+60.
t+60.
(2)A点的坐标是A( ,
,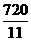 ),点A是
),点A是 和y2=
和y2=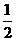 t+60的交点;B点的坐标是B(
t+60的交点;B点的坐标是B(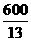 ,
,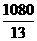 ),点B是
),点B是 和y2=
和y2=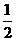 t+60的交点.
t+60的交点.
(3)补全图象如下:

15. (2011山东潍坊,21,10分)2011年秋冬北方严重干旱,凤凰社区人畜饮用水紧张,每天需从社区外调运饮用水120吨.有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨.从两水厂运水到凤凰社区供水点的路程和运费如下表:

(1)若某天调运水的总运费为26700元,则从甲、乙两水厂各调运了多少吨饮用水?
(2)设从甲厂调运饮用水x吨,总运费为W元,试写出W关于与x的函数关系式,怎样安排调运方案才能是每天的总运费最省?
[解](1)设从甲厂调运饮用水x吨,从乙厂调运饮用水y吨,根据题意得

解得
∵50 80,70
80,70 90,∴符合条件.
90,∴符合条件.
故从甲、乙两水厂各调用了50吨、70吨饮用水.
(2)设从甲厂调运饮用水x吨,则需从乙厂调运水(120-x)吨,根据题意可得
 解得
解得 .
.
总运费 ,(
,( )
)
∵W随x的增大而增大,故当 时,
时, 元.
元.
∴每天从甲厂调运30吨,从乙厂调运90吨,每天的总运费最省.
14. (2011山东济宁,21,8分)“五一”期间,为了满足广大人民的消费需求,某商店计划用160000元购进一批家电,这批家电的进价和售价如下表:
|
类别 |
彩电 |
冰箱 |
洗衣机 |
|
进价 |
2000 |
1600 |
1000 |
|
售价 |
2200 |
1800 |
1100 |
(1)若全部资金用来购买彩电和洗衣机共100台,问商家可以购买彩电和洗衣机各多少台?
(2)若在现有资金160000元允许的范围内,购买上表中三类家电共100台,其中彩电台数和冰箱台数相同,且购买洗衣机的台数不超过购买彩电的台数,请你算一算有几种进货方案?哪种进货方案能使商店销售完这批家电后获得的利润最大?并求出最大利润.(利润=售价-进价)
[答案]解:(1)设商家购买彩电x台,则购买洗衣机(100-x)台,
由题意,得 2000x+1000(100-x)=160000,解得x=60.
则100-x=40(台),
所以,商家可以购买彩电60台,洗衣机40台.
(2)设购买彩电a台,则够买洗衣机为(100-2a)台,
根据题意,得
解得 ,因为a是整数,所以a=34,35,36,37.
,因为a是整数,所以a=34,35,36,37.
因此,共有四种进货方案.
设商店销售完毕后获得利润为w元.
则 w=(2200-2000)a+(1800-1600)a+(1100-1000)(100-2a)
=200a+10000.
∵200>0,∴w随a的增大而增大,∴当a=37时,
w最大值=200×37+10000=17400元
所以商店获取利润最大为17400元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com