
题目列表(包括答案和解析)
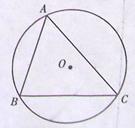
10.(2011江西,21,8分)如图,已知⊙O的半径为2,弦BC的长为 ,点A为弦BC所对优弧上任意一点(B,C两点除外)。
,点A为弦BC所对优弧上任意一点(B,C两点除外)。
⑴求∠BAC的度数;
⑵求△ABC面积的最大值.
(参考数据:sin60°=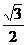 ,cos30°=
,cos30°=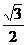 ,tan30°=
,tan30°= .)
.)
[答案](1)过点O作OD⊥BC于点D, 连接OA.
因为BC= ,所以CD=
,所以CD=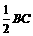 =
= .
.
又OC=2,所以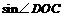 =
=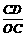 ,即
,即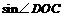 =
=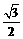 ,
,
所以∠DOC=60°.
又OD⊥BC,所以∠BAC=∠DOC=60°.
(2)因为△ABC中的边BC的长不变,所以底边上的高最大时,△ABC面积的最大值,即点A是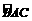 的中点时,△ABC面积的最大值.
的中点时,△ABC面积的最大值.
因为∠BAC=60°,所以△ABC是等边三角形,
在Rt△ADC中,AC= ,DC=
,DC= ,
,
所以AD=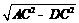 =
=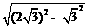 =3.
=3.
所以△ABC面积的最大值为 ×3×
×3×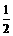 =3
=3 .
.
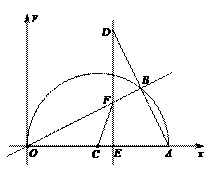
9. (2011浙江丽水,24,12分)如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.
(1)当∠AOB=30°时,求弧AB的长;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似,若存在,请求出此时点E的坐标;若不存在,请说明理由.
[解](1)连结BC,

∵A(10,0),∴OA=10,CA=5,
∵∠AOB=30°,
 ∴∠ACB=2∠AOB=60°,
∴∠ACB=2∠AOB=60°,
∴的长==;
(2)连结OD,

∵OA是⊙C的直径,∴∠OBA=90°,
又∵AB= BD,
∴OB是AD的垂直平分线,
∴OD= OA=10,
在Rt△ODE中,
OE===6,
∴AE= AO-OE =10-6=4,
由∠AOB=∠ADE= 90°-∠OAB,
∠OEF=∠DEA,
得△OEF∽△DEA,
∴=,即=,∴EF=3;


(3)设OE=x,
①当交点E在O,C之间时,由以点E、C、F为顶点的三角形与△AOB相似,
有∠ECF=∠BOA或∠ECF=∠OAB,当∠ECF=∠BOA时,此时△OCF为等腰三角形,
点E为OC的中点,即OE=,
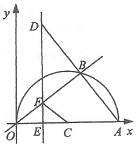
∴E1(,0);
当∠ECF=∠OAB时,有CE=5-x,AE=10-x,
∴CF//AB,有CF=AB,
∵△ECF∽△EAD,
∴=,即=,解得x=,
∴E2(,0);
②当交点E在C的右侧时,
∵∠ECF>∠BOA
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO,
连结BE,
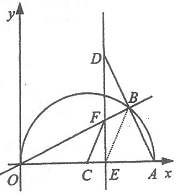
∵BE为Rt△ADE斜边上的中线,
∴BE=AB=BD,
∴∠BEA=∠BAO,
∴∠BEA=∠ECF,
∵CF//BE,∴=,
∵∠ECF=∠BAO,∠FEC=∠DEA=Rt∠,
∴△CEF∽△AED,∴=,
而AD=2BE,∴=,
即=,
解得x1=,x2=<0(舍去),
∴E3(,0);
③当交点E在O的左侧时,
∵∠BOA=∠EOF>∠ECF
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO,
连结BE,得BE=AD=AB,
∠BEA=∠BAO,
∴∠ECF=∠BEA,
∴CF//BE,
∴=,
又∵∠ECF=∠BAO,∠FEC=∠DEA=Rt∠,
∴△CEF∽△AED,∴=,
而AD=2BE,∴=,
∴=,解得x1=,x2=<0(舍去),
∵点E在x轴负半轴上,∴E4(,0),
综上所述:存在以点E、C、F为顶点的三角形与△AOB相似,此时点E坐标为:
∴E1(,0)、E2(,0)、E3(,0)、E4(,0).
8. (2011广东广州市,25,14分)
如图7,⊙O中AB是直径,C是⊙O上一点,∠ABC=45°,等腰直角三角形DCE中 ∠DCE是直角,点D在线段AC上.
(1)证明:B、C、E三点共线;
(2)若M是线段BE的中点,N是线段AD的中点,证明:MN=OM;
(3)将△DCE绕点C逆时针旋转α(0°<α<90°)后,记为△D1CE1(图8),若M1是线段BE1的中点,N1是线段AD1的中点,M1N1=OM1是否成立?若是,请证明;若不是,说明理由.
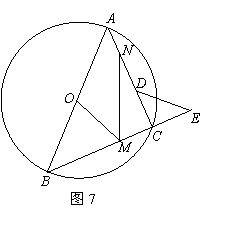

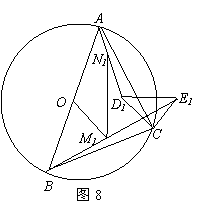

[答案](1)∵AB为⊙O直径
∴∠ACB=90°
∵△DCE为等腰直角三角形
∴∠ACE=90°
∴∠BCE=90°+90°=180°
∴B、C、E三点共线.
(2)连接BD,AE,ON.
∵∠ACB=90°,∠ABC=45°
∴AB=AC
∵DC=DE
∠ACB=∠ACE=90°
∴△BCD≌△ACE
∴AE=BD,∠DBE=∠EAC
∴∠DBE+∠BEA=90°
∴BD⊥AE
∵O,N为中点
∴ON∥BD,ON=BD
同理OM∥AE,OM=AE
∴OM⊥ON,OM=ON
∴MN=OM
(3)成立
证明:同(2)旋转后∠BCD1=∠BCE1=90°-∠ACD1
所以仍有△BCD1≌△ACE1,
所以△ACE1是由△BCD1绕点C顺时针旋转90°而得到的,故BD1⊥AE1
其余证明过程与(2)完全相同.
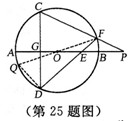
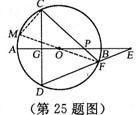
7. (2011浙江丽水,21,8分)如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE.
(1)求证:AP=AO;
(2)若弦AB=12,求tan∠OPB的值;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为 ,能构成等腰梯形的四个点为 或 或 .
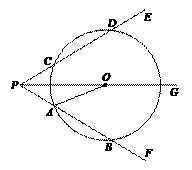
[解](1)∵PG平分∠EPF,
∴∠DPO=∠BPO,
∵OA//PE,
∴∠DPO=∠POA,
∴∠BPO=∠POA,
∴PA=OA;
(2)过点O作OH⊥AB于点H,则AH=HB,
∵AB=12,
∴AH=6,
由(1)可知PA=OA=10,
∴PH=PA+AH=16,
OH==8,
∴tan∠OPB==;
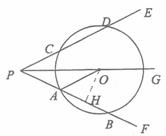
(3)P、A、O、C;A、B、D、C或P、A、O、D或P、C、O、B.
5. (2011山东烟台,25,12分)已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:OE·OP=r2
(2)当点E在AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
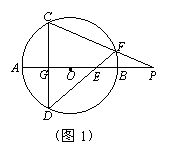

[答案](1)证明:连接FO并延长交⊙O于Q,连接DQ.
 ∵FQ是⊙O直径,∴∠FDQ=90°.
∵FQ是⊙O直径,∴∠FDQ=90°.
∴∠QFD+∠Q=90°.
∵CD⊥AB,∴∠P+∠C=90°.
∵∠Q=∠C,∴∠QFD=∠P.
∵∠FOE=∠POF,∴△FOE∽△POF.
∴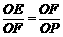 .∴OE·OP=OF2=r2.
.∴OE·OP=OF2=r2.
(2)解:(1)中的结论成立.
 理由:如图2,依题意画出图形,连接FO并延长交⊙O于M,连接CM.
理由:如图2,依题意画出图形,连接FO并延长交⊙O于M,连接CM.
∵FM是⊙O直径,∴∠FCM=90°,∴∠M+∠CFM=90°.
∵CD⊥AB,∴∠E+∠D=90°.
∵∠M=∠D,∴∠CFM=∠E.
∵∠POF=∠FOE,∴△POF∽△FOE.
∴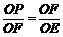 ,∴OE·OP=OF2=r2.
,∴OE·OP=OF2=r2.
4. (2011山东济宁,19,6分)如图, 为
为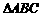 外接圆的直径,
外接圆的直径,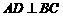 ,垂足为点
,垂足为点 ,
,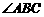 的平分线交
的平分线交 于点
于点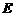 ,连接
,连接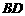 ,
, .
.
(1) 求证: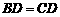 ;
;
(2) 请判断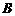 ,
,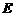 ,
,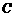 三点是否在以
三点是否在以 为圆心,以
为圆心,以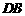 为半径的圆上?并说明理由.
为半径的圆上?并说明理由.


[答案](1)证明:∵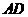 为直径,
为直径,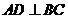 ,
,
∴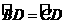 .∴
.∴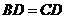 . ································································· 3分
. ································································· 3分
(2)答: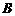 ,
,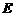 ,
,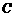 三点在以
三点在以 为圆心,以
为圆心,以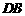 为半径的圆上. ···························· 4分
为半径的圆上. ···························· 4分
理由:由(1)知: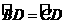 ,∴
,∴ .
.
∵ ,
,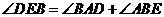 ,
, ,
,
∴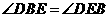 .∴
.∴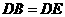 .··································································· 6分
.··································································· 6分
由(1)知: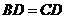 .∴
.∴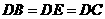 .
.
∴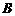 ,
,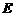 ,
,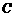 三点在以
三点在以 为圆心,以
为圆心,以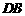 为半径的圆上. …………………7分
为半径的圆上. …………………7分
3. (2011山东德州22,10分)●观察计算
当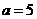 ,
,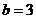 时,
时, 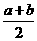 与
与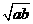 的大小关系是_________________.
的大小关系是_________________.
当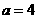 ,
, 时,
时, 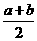 与
与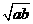 的大小关系是_________________.
的大小关系是_________________.
●探究证明
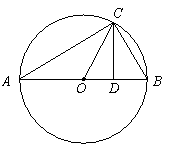
如图所示,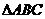 为圆O的内接三角形,
为圆O的内接三角形,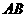 为直径,过C作
为直径,过C作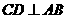 于D,设
于D,设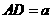 ,BD=b.
,BD=b.
(1)分别用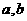 表示线段OC,CD;
表示线段OC,CD;
(2)探求OC与CD表达式之间存在的关系
(用含a,b的式子表示).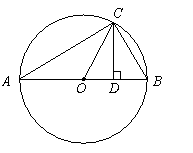

●归纳结论
根据上面的观察计算、探究证明,你能得出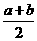 与
与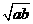 的大小关系是:_________________________.
的大小关系是:_________________________.
●实践应用
要制作面积为1平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
[答案]●观察计算: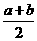 >
>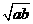 ,
, 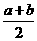 =
=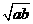 . …………………2分
. …………………2分
 ●探究证明:
●探究证明:
(1)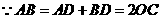 ,
,
∴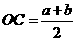 …………………3分
…………………3分
 AB为⊙O直径,
AB为⊙O直径,
∴ .
.
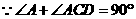 ,
,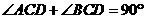 ,
,
∴∠A=∠BCD.
∴△ ∽△
∽△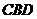 . …………………4分
. …………………4分
∴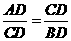 .
.
即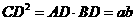 ,
,
∴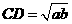 .
…………………5分
.
…………………5分
(2)当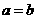 时,
时,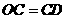 ,
, 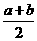 =
=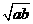 ;
;
 时,
时, ,
, 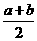 >
>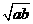 .…………………6分
.…………………6分
●结论归纳: 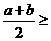
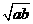 . ………………7分
. ………………7分
●实践应用
设长方形一边长为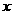 米,则另一边长为
米,则另一边长为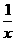 米,设镜框周长为l米,则
米,设镜框周长为l米,则
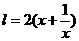 ≥
≥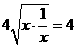 .
……………9分
.
……………9分
当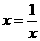 ,即
,即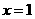 (米)时,镜框周长最小.
(米)时,镜框周长最小.
此时四边形为正方形时,周长最小为4 米. ………………10分
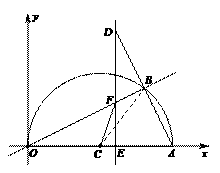
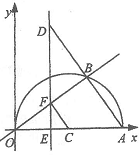
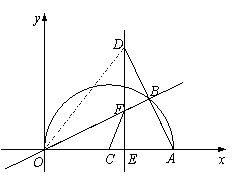
2.(2011浙江金华,24,12分)如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上的一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.
(1)当∠AOB=30°时,求弧AB的长;
(2)当DE=8时,求线段EF的长;
(3)在点B运动过程中,是否存在以点E、C、F为顶点的三角形与△AOB相似,若存在,请求出此时点E的坐标;若不存在,请说明理由.
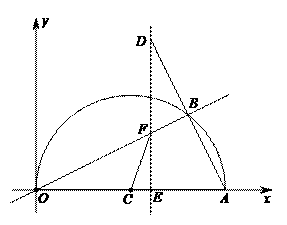
解:(1)连结BC,
∵A(10,0), ∴OA=10 ,CA=5,
∵∠AOB=30°,
∴∠ACB=2∠AOB=60°,
∴弧AB的长=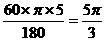 ; ……4分
; ……4分

(2)连结OD,
∵OA是⊙C直径, ∴∠OBA=90°,
又∵AB=BD,
∴OB是AD的垂直平分线,
∴OD=OA=10,
在Rt△ODE中,
OE=
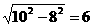 ,
,
∴AE=AO-OE=10-6=4,
由 ∠AOB=∠ADE=90°-∠OAB,∠OEF=∠DEA,
得△OEF∽△DEA,
∴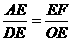 ,即
,即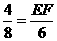 ,∴EF=3;……4分
,∴EF=3;……4分
(3)设OE=x,
①当交点E在O,C之间时,由以点E、C、F为顶点的三角形与△AOB相似,有∠ECF=∠BOA或∠ECF=∠OAB,当∠ECF=∠BOA时,此时△OCF为等腰三角形,点E为OC中点,即OE=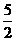 ,
,
∴E1(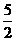 ,0);
,0);
当∠ECF=∠OAB时,有CE=5-x, AE=10-x,
∴CF∥AB,有CF=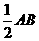 ,
,
∵△ECF∽△EAD,
∴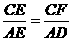 ,即
,即 ,解得:
,解得: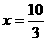 ,
,
∴E2(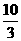 ,0);
,0);




②当交点E在点C的右侧时,
∵∠ECF>∠BOA,
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO,
连结BE,
∵BE为Rt△ADE斜边上的中线,
∴BE=AB=BD,
∴∠BEA=∠BAO,
∴∠BEA=∠ECF,
∴CF∥BE, ∴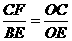 ,
,
∵∠ECF=∠BAO, ∠FEC=∠DEA=Rt∠,
∴△CEF∽△AED, ∴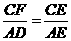 ,
,
而AD=2BE, ∴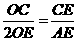 ,
,
即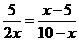 , 解得
, 解得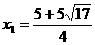 ,
, 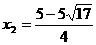 <0(舍去),
<0(舍去),
∴E3( ,0);
,0);


③当交点E在点O的左侧时,
∵∠BOA=∠EOF>∠ECF .
∴要使△ECF与△BAO相似,只能使∠ECF=∠BAO
连结BE,得BE=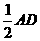 =AB,∠BEA=∠BAO
=AB,∠BEA=∠BAO
∴∠ECF=∠BEA,
∴CF∥BE,
∴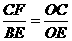 ,
,
又∵∠ECF=∠BAO, ∠FEC=∠DEA=Rt∠,
∴△CEF∽△AED, ∴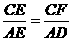 ,
,
而AD=2BE, ∴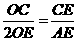 ,
,
∴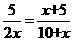 , 解得
, 解得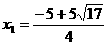 ,
, 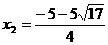 <0(舍去),
<0(舍去),
∵点E在x轴负半轴上, ∴E4(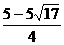 ,0),
,0),
综上所述:存在以点E、C、F为顶点的三角形与△AOB相似,此时点E坐标为:
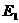 (
(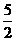 ,0)、
,0)、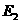 (
(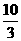 ,0)、
,0)、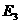 (
( ,0)、
,0)、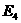 (
(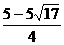 ,0).……4分
,0).……4分


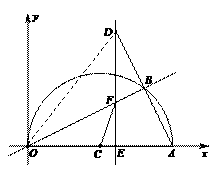
1. (2011浙江金华,21,8分)如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF两边相交于A、B和C、D,连结OA,此时有OA∥PE.
(1)求证:AP=AO;
(2)若弦AB=12,求tan∠OPB的值;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为 ,能构成等腰梯形的四个点为 或 或 .

证明:(1)∵PG平分∠EPF,
∴∠DPO=∠BPO ,
∵OA//PE,
∴∠DPO=∠POA ,
∴∠BPO=∠POA,
∴PA=OA; ……2分
解:(2)过点O作OH⊥AB于点H,则AH=HB=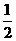 AB,……1分
AB,……1分
∵ tan∠OPB=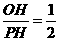 ,∴PH=2OH, ……1分
,∴PH=2OH, ……1分
设OH=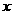 ,则PH=2
,则PH=2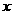 ,
,
由(1)可知PA=OA=
10 ,∴AH=PH-PA=2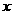 -10,
-10,
∵ , ∴
, ∴ , ……1分
, ……1分
解得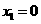 (不合题意,舍去),
(不合题意,舍去),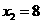 ,
,
∴AH=6, ∴AB=2AH=12; ……1分
(3)P、A、O、C;A、B、D、C 或 P、A、O、D 或P、C、O、B.……2分(写对1个、2个、3个得1分,写对4个得2分)


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com