
题目列表(包括答案和解析)
20.(2011广东茂名,24,8分)如图,⊙P与 轴相切于坐标原点O(0,0),与
轴相切于坐标原点O(0,0),与 轴相交于点A(5,0),过点A的直线AB与
轴相交于点A(5,0),过点A的直线AB与 轴的正半轴交于点B,与⊙P交于点C.
轴的正半轴交于点B,与⊙P交于点C.
(1)已知AC=3,求点B的坐标; (4分)
(2)若AC= , D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同一圆上,记这个圆的圆心为
, D是OB的中点.问:点O、P、C、D四点是否在同一圆上?请说明理由.如果这四点在同一圆上,记这个圆的圆心为 ,函数
,函数 的图象经过点
的图象经过点 ,求
,求 的值(用含
的值(用含 的代数式表示).
(4分)
的代数式表示).
(4分)




[答案]解:(1)解法一:连接OC,∵OA是⊙P的直径,∴OC⊥AB,
在Rt△AOC中,
在 Rt△AOC和Rt△ABO中,∵∠CAO=∠OAB
∴Rt△AOC∽Rt△ABO,·
∴ ,即
,即 ,
,
∴ , ∴
, ∴
解法二:连接OC,因为OA是⊙P的直径, ∴∠ACO=90°
在Rt△AOC中,AO=5,AC=3,∴OC=4,
过C作CE⊥OA于点E,则: ,
,
即: ,∴
,∴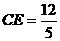 ,
,
∴ ∴
∴ ,
,

设经过A、C两点的直线解析式为: .
.
把点A(5,0)、 代入上式得:
代入上式得:
 , 解得:
, 解得: ,
,
∴ , ∴点
, ∴点 .
.
(2)点O、P、C、D四点在同一个圆上,理由如下:
连接CP、CD、DP,∵OC⊥AB,D为OB上的中点,
∴ ,
,
∴∠3=∠4,又∵OP=CP,∴∠1=∠2,∴∠1+∠3=∠2+∠4=90°,
∴PC ⊥CD,又∵DO⊥OP,∴Rt△PDO和Rt△PDC是同以PD为斜边的直角三角形,∴PD上的中点到点O、P、C、D四点的距离相等,
∴点O、P、C、D在以DP为直径的同一个圆上;
由上可知,经过点O、P、C、D的圆心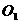 是DP的中点,圆心
是DP的中点,圆心 ,
,
由(1)知:Rt△AOC∽Rt△ABO,∴ ,求得:AB=
,求得:AB=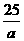 ,在Rt△ABO中,
,在Rt△ABO中,
 ,OD=
,OD= ,
,
∴ ,点
,点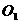 在函数
在函数 的图象上,
的图象上,
∴ ,
∴
,
∴
 .
.
19. (2011湖北黄冈,22,8分)在圆内接四边形ABCD中,CD为∠BCA外角的平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于E.
⑴求证△ABD为等腰三角形.
⑵求证AC•AF=DF•FE
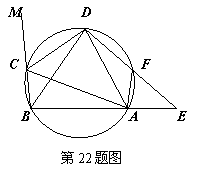

[答案]⑴由圆的性质知∠MCD=∠DAB、∠DCA=∠DBA,而∠MCD=∠DCA,所以∠DBA=∠DAB,故△ABD为等腰三角形.
⑵∵∠DBA=∠DAB
∴弧AD=弧BD
又∵BC=AF
∴弧BC=弧AF、∠CDB=∠FDA
∴弧CD=弧DF
∴CD=DF
再由“圆的内接四边形外角等于它的内对角”知
∠AFE=∠DBA=∠DCA①,∠FAE=∠BDE
∴∠CDA=∠CDB+∠BDA=∠FDA+∠BDA=∠BDE=∠FAE② 由①②得△DCA∽△FAE
∴AC:FE=CD:AF
∴AC•AF= CD •FE
而CD=DF,
∴AC•AF=DF•FE
18. (2011上海,21,10分)如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=2,CD平行于AB,并与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若 ,求弦MN的长.
,求弦MN的长.

[答案](1)∵CD∥AB,
∴∠OAB=∠C,∠OBA=∠D.
∵OA=OB,
∴∠OAB=∠OBA.
∴∠C=∠D.
∴OC=OD.
∵OA=3,AC=2,
∴OC=5.
∴OD=5.
(2)过点O作OE⊥CD,E为垂足,连接OM.


在Rt△OCE中,OC=5, ,设OE=x,则CE=2x.由勾股定理得
,设OE=x,则CE=2x.由勾股定理得 ,解得x1=
,解得x1= ,x2=
,x2= (舍去).∴OE=
(舍去).∴OE= .
.
在Rt△OME中,OM=OA=3,ME= =
= =2。∴MN=2ME=4.
=2。∴MN=2ME=4.
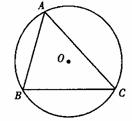
17. (2011江西南昌,21,8分)如图,已知⊙O的半径为2,弦BC的长为 ,点A为弦BC所对优弧上任意一点(B,C两点除外)。
,点A为弦BC所对优弧上任意一点(B,C两点除外)。
⑴求∠BAC的度数;
⑵求△ABC面积的最大值.
(参考数据:sin60°= ,cos30°=
,cos30°= ,tan30°=
,tan30°= .)
.)
[答案](1)过点O作OD⊥BC于点D, 连接OA.
因为BC= ,所以CD=
,所以CD= =
= .
.
又OC=2,所以 =
= ,即
,即 =
= ,
,
所以∠DOC=60°.
又OD⊥BC,所以∠BAC=∠DOC=60°.
(2)因为△ABC中的边BC的长不变,所以底边上的高最大时,△ABC面积的最大值,即点A是 的中点时,△ABC面积的最大值.
的中点时,△ABC面积的最大值.
因为∠BAC=60°,所以△ABC是等边三角形,
在Rt△ADC中,AC= ,DC=
,DC= ,
,
所以AD= =
=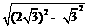 =3.
=3.
所以△ABC面积的最大值为 ×3×
×3× =3
=3 .
.
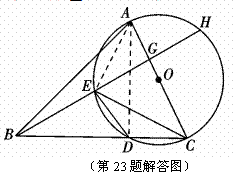
16. (2011四川宜宾,23,10分)已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧 ⌒ AD上到一点E使∠EBC=∠DEC,延长BE依次交AC于G,交⊙O于H.
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.


[答案]证明:⑴连接AD
∵∠DAC=∠DEC ∠EBC=∠DEC
∴∠DAC=∠EBC
又∵AC是⊙O的直径
∴∠ADC=90°
∴∠DCA+∠DAC=90°
∴∠EBC+∠DCA=90°
∴∠BGC=180°-(∠EBC+∠DCA)=180°-90°=90°
∴AC⊥BH
⑵∵∠BDA=180°-∠ADC=90°∠ABC=45°
∴∠BAD=45°
∴BD=AD
∵BD=8
∴AD=8
又∵∠ADC=90° AC=10

∴由勾股定理,得 .
.
∴BC=BD+DC=8+6=14
又∵∠BGC=∠ADC=90° ∠BCG=∠ACD
∴△BCG∽△ACD
∴
∴ ∴
∴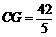
连接AE,∵AC是直径 ∴∠AEC=90°
又∵EG⊥AC
∴△CEG∽△CAE ∴ ∴
∴
∴ .
.
15. (2011四川成都,27,10分)已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙0,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
 (1)求证:AE=CK;
(1)求证:AE=CK;
(2)如果AB= ,AD=
,AD= (
( 为大于零的常数),求BK的长;
为大于零的常数),求BK的长;
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.
[答案]
解:(1)∵DH∥KB,BK⊥AC,∴DE⊥AC,
∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∴∠EAD=∠KCB,
∴Rt△ADE≌Rt△CBK,∴AE=CK.
(2)在Rt△ABC中,AB= ,AD=BC=
,AD=BC= ,∴
,∴ =
= =
= ,
,
 ∵S△ABC=
∵S△ABC= AB×BC=
AB×BC= AC×BK,∴BK=
AC×BK,∴BK= =
= =
= .
.
(3)连线OG,∵AC⊥DG,AC是⊙O的直接,DE=6,∴DE=EG=6,又∵EF=FG,∴EF=3;∵Rt△ADE≌Rt△CBK,∴DE=BK=6,AE=CK,
在△ABK中,EF=3,BK=6,EF∥BK,∴EF是△ABK的中位线,∴AF=BF,AE=EK=KC;在Rt△OEG中,设OG= ,则OE=
,则OE= ,EG=6,
,EG=6, ,∴
,∴ ,∴
,∴ .
.
在Rt△ADF≌Rt△BHF中,AF=BF,
∵AD=BC,BF∥CD,∴HF=DF,
∵FG=EF,∴HF-FG=DF-EF,∴HG=DE=6.
14. (2011江苏泰州,26,10分)如图,以点O为圆心的两个同心圆中,矩形ABCD的边BC为大圆的弦,边AD与小圆相切于点M,OM的延长线与BC相交于点N.
(1)点N是线段BC的中点吗?为什么?
(2)若圆环的宽度(两圆半径之差)为6cm,AB=5cm,BC=10cm,求小圆的半径.
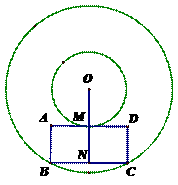
[答案]解:(1)N是BC的中点。原因:∵AD与小圆相切于点M,
∴OM⊥AD,又AD∥BC,∴ON⊥BC,∴在大圆O中,由垂径定理可得N是BC的中点.
(2)连接OB,设小圆半径为r,则有ON=r+5,OB=r+6,BN=5cm,
在Rt△OBN中,由勾股定理得OB2=BN2+ON2 ,即:(r+6)2=(r+5)2+52 ,解得r=7cm.
∴小圆的半径为7cm.
13. (2011江苏苏州,27,8分)已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD.
(1)如图①,当PA的长度等于______时,∠PAB=60°;
当PA的长度等于______时,△PAD是等腰三角形;
(2)如图②,以AB边所在的直线为x轴,AD边所在的直线为y轴,建立如图所示的直角坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3.设P点坐标为(a,b),试求2S1S3-S22的最大值,并求出此时a、b的值.

[答案]解:(1)2;2 或
或 .
.
(2)如图,过点P分别作PE⊥AB,PF⊥AD,垂足分别为E、F,延长FP交BC于点G,则PG⊥BC.
∵P点坐标为(a,b),∴PE=b,PF=a,PG=4-a.
在△PAD、△PAB及△PBC中,
S1=2a,S2=2b,S3=8-2a,
∵AB是直径,∴∠APB=90°.
∴PE2=AE·BE,即b2=a(4-a).
∴2S1S3-S22=4a(8-2a)-4b2=-4a2+16a=-4(a-2)2+16.
∴当a=2时,b=2,2S1S3-S22有最大值16.

12. (2011江苏苏州,26,8分)如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)弦长AB=________(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以点A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似?请写出解答过程.

[答案]解:(1)2 .
.
(2)解法一:∵∠BOD是△BOC的外角,∠BCO是△ACD的外角,
∴∠BOD=∠B+∠BCO,∠BCO=∠A+∠D.
∴∠BOD=∠B+∠A+∠D.
又∵∠BOD=2∠A,∠B=30°,∠D=20°,
∴2∠A=∠B+∠A+∠D=∠A+50°,∠A=50°,
∴∠BOD=2∠A=100°.
解法二:如图,连接OA.
∵OA=OB,OA=OD,∴∠BAO=∠B,∠DAO=∠D,
∴∠DAB=∠BAO+∠DAO=∠B+∠D.
又∵∠B=30°,∠D=20°,∴∠DAB=50°,
∴∠BOD=2∠DAB=100°.

(3)∵∠BCO=∠A+∠D,∴∠BCO>∠A,∠BCO>∠D.
∴要使△DAC与△BOC相似,只能∠DCA=∠BCO=90°.
此时,∠BOC=60°,∠BOD=120°,∴∠DAC=60°.
∴△DAC∽△BOC.
∵∠BCO=90°,即OC⊥AB,∴AC= AB=
AB= .
.
11. (2011湖南常德,25,10分)已知
△ABC,分别以AC和BC为直径作半圆 、
、 P是AB的中点.
P是AB的中点.
(1)如图8,若△ABC是等腰三角形,且AC=BC,在 上分别取点E、F,使
上分别取点E、F,使 则有结论①
则有结论① 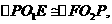 ②四边形
②四边形 是菱形.请给出结论②的证明;
是菱形.请给出结论②的证明;
(2)如图9,若(1)中△ABC是任意三角形,其它条件不变,则(1)中的两个结论还成立吗?若成立,请给出证明;
(3)如图10,若PC是 的切线,求证:
的切线,求证:


[答案]
(1) 证明:∵BC是⊙O2直径,则O2是BC的中点
又P是AB的中点.
∴P O2是△ABC的中位线
∴P O2 =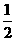 AC
AC
又AC是⊙O1直径
∴P O2= O1C=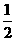 AC
AC
同理P O1= O2C =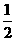 BC
BC
∵AC =BC
∴P O2= O1C=P O1= O2C
∴四边形 是菱形
是菱形
(2)
结论①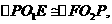 成立,结论②不成立
成立,结论②不成立
证明:在(1)中已证PO2=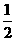 AC,又O1E=
AC,又O1E=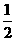 AC
AC
∴PO2=O1E
同理可得PO1=O2F
∵PO2是△ABC的中位线
∴PO2∥AC
∴∠PO2B=∠ACB
同理∠P O1A=∠ACB
∴∠PO2B=∠P O1A
∵∠AO1E =∠BO2F
∴∠P O1A+∠AO1E =∠PO2B+∠BO2F
即∠P O1E =∠F O2 P
∴
(3) 证明:延长AC交⊙O2于点D,连接BD.
∵BC是⊙O2的直径,则∠D=90°,
又PC是 的切线,则∠ACP=90°,
的切线,则∠ACP=90°,
∴∠ACP=∠D
又∠PAC=∠BAD,
∴△APC∽△BAD
又P是AB的中点
∴
∴AC=CD
∴在Rt△BCD中,
在Rt△ABD中,
∴
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com