9. (2011广东茂名，18，7分)画图题：

(1)如图，将△ABC绕点O顺时针旋转180°后得到△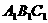.请你画出旋转后的△ 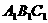；　 (3分)　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　(2)请你画出下面“蒙古包”的左视图．(4分)

　

[答案]解：如图所示：(1)画对得3分；(2)画对得4分(说明：图形基本正确给满分，如果没有画出线段CD扣1分；如果把线段AB、CD画成弧线也各扣1分，考生可以不用标出字母A、B、C、D)．

　　

8. (2011湖北武汉市，21，7分)(本题满分7分)在平面直角坐标系中，△ABC的顶点坐标是A(－7，1)，B(1，1)，C(1，7)．线段DE的端点坐标是D(7，－1)，E(－1，－7)．

(1)试说明如何平移线段AC，使其与线段ED重合；

(2)将△ABC绕坐标原点O逆时针旋转，使AC的对应边为DE，请直接写出点B的对应点F的坐标；

(3)画出(2)中的△DEF，并和△ABC同时绕坐标原点O逆时针旋转90°，画出旋转后的图形．

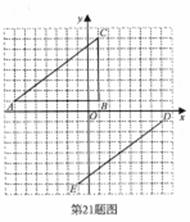
[答案](1)将线段AC先向右平移6个单位，

再向下平移8个单位．(其它平移方式也可)

(2)F(－1,－1)

(3)画出如图所示的正确图形

　　

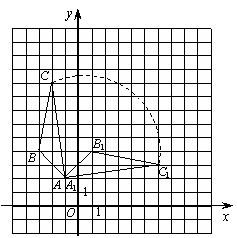
7. (2011四川凉山州，21，8分)在平面直角坐标系中，已知三个顶点的坐标分别为

⑴画出，并求出所在直线的解析式。

⑵画出绕点顺时针旋转后得到的，并求出在上述旋转过程中扫过的面积。

[答案]

⑴如图所示，即为所求　　　

　设所在直线的解析式为

　∵，

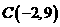
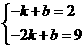　∴　 解得

　∴　　

　⑵如图所示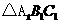，即为所求　

　　　　 由图可知，　

　　

　　　　　 =

6. (2011山东聊城，20，8分)将两块大小相同的含30°角的直角三角板(∠BAC＝∠B′A′C＝30°)按图①方式放置，固定三角板A′B′C，然后将三角板ABC绕直角顶点C顺时针方向旋转(旋转角小于90°)至图②所示的位置，AB与A′C交于点E，AC与A′B′交于点F，AB与A′B′相交于点O．

(1)求证：△BCE≌△B′CF；

(2)当旋转角等于30°时，AB与A′B′垂直吗？请说明理由．

[答案](1)因∠B＝∠B^/，BC＝B^/C，∠BCE＝∠B^/CF，所以△BCE≌△B′CF；

(2)AB与A′B′垂直，理由如下：

旋转角等于30°，即∠ECF＝30°，所以∠FCB^/＝60°，又∠B＝∠B^/＝60°，根据四边形的内角和可知∠BOB^/的度数为360°－60°－60°－150°＝90°，所以AB与A′B′垂直

5. (2011山东济宁，22，8分)去冬今春，济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题，要在某河道建一座水泵站，分别向河的同一侧张村A和李村B送水．经实地勘查后，工程人员设计图纸时，以河道上的大桥O为坐标原点，以河道所在的直线为x轴建立直角坐标系(如图)，两村的坐标分别为A(2，3)，B(12，7)．

(1)若从节约经费考虑，水泵站建在距离大桥O多远的地方可使所用输水管最短?

(2)水泵站建在距离大桥O多远的地方，可使它到张村、李村的距离相等？

[答案]解：(1)作点B关于x轴的对称点E，连接AE，

则点E为(12，－7)，

设直线AE的函数关系式为y=kx+b，则

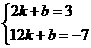，解得，

所以，直线AE解析式为y=－x+5

　　　　　　　 当y=0时，x=5，所以，水泵站应建在距离大桥5千米的地方时，可使所用输水管道最短．

　　　　　　 (2)作线段AB的垂直平分线GF，交AB 于点F，交x轴于点G，

　　　　　　 设点G的坐标为(x，0)，

　　　　　　　　 在Rt△AGD中，AG²=AD²+DG²=3²+(x－2)²

　　　 　　　　　在Rt△BCG中，BG²=BC²+GC²=7²+(12－x)²

　　　　　 　 ∵AG= BG，∴3²+(x－2)²=7²+(12－x)²

　　　　 　解得x=9．

　　　　　　 所以，水泵站建在距离大桥9千米的地方，可使它到张村、李村的距离相等．

4. (2011浙江绍兴，18，8分)分别按下列要求解答：

(1)在图1中，作出关于直线成轴对称的图形；(2)在图2中，作出关于点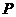成中心对称的图形.

第18题图2

第18题图1

　　

[答案](1)如图1；

　　　 (2)如图2

第18题图1

第18题图2

3. (2011浙江杭州，21， 8)在平面上，七个边长均为1的等边三角形，分别用①至⑦表示(如图)．从④⑤⑥⑦组成的图形中，取出一个三角形，使剩下的图形经过一次平移，与①②③组成的图形拼成一个正六边形．

(1)你取出的是哪个三角形？写出平移的方向和平移的距离；

(2)将取出的三角形任意放置在拼成的正六边形所在平面上，问：正六边形没有被三角形盖住的面积能否等于?请说明理由．

[答案](1)当取出的是⑦时，将剩下的图形向上平移1(如图1)；当取出的是⑤时，将⑥⑦向上平移2(如图2)

　　

(2)能．每个小等边三角形的面积为，五个小等边三角形的面积和为，正六边形的面积为，而，所以正六边形没有被三角形盖住的面积能等于．

2. (2011安徽，22，12分)在△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕顶点C顺时针旋转，旋转角为(0°＜＜180°)，得到△A′B′C．

(1)如图(1)，当AB∥CB′时，设A′B′与CB相交于点D．

证明：△A′CD是等边三角形；

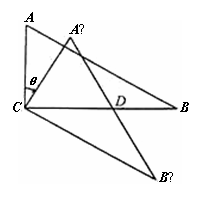
(2)如图(2)，连接A′A、B′B，设△ACA′ 和△BCB′ 的面积分别为S_△ACA′ 和S_△BCB′．

求证：S_△ACA′ ：S_△BCB′ =1：3；

(3)如图(3)，设AC中点为E，A′B′中点为P，AC=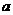，连接EP，当=　　　　 °时，EP长度最大，最大值为　　　　 ．

[答案](1)∵AB∥CB′，∴∠B=∠BC B′=30°，∴∠A′CD=60°，

又∵∠A′=60°，∴∠A′CD=∠A′=∠A′DC=60°，∴△A′CD是等边三角形；

　　　　　 (2)∵∠ACA′=∠BCB′，AC=A′C，BC=B′C，∴△ACA′∽△BCB′，相似比为，

∴S_△ACA′ ：S_△BCB′ =1：3；

(3)120°，．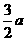

当E、C、P三点不共线时，EC+CP>EP；

当E、C、P三点共线时，EC+CP=EP；

综上所述，EP≤EC+CP；

则当旋转120°时，E、C、P三点共线，EP长度最大，此时EP=EC+CP=．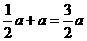

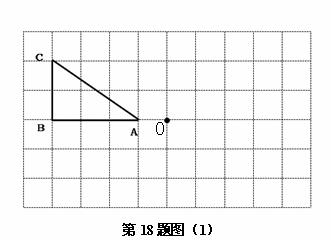
1. (2011安徽，17，8分)如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A₁B₁C₁和△A₂B₂C₂；

(1)将△ABC向右平移4个单位，再向上平移1个单位，得到△A₁B₁C₁；

(2)以图中的O为位似中心，将△A₁B₁C₁作位似变换且放大到原来的两倍，得到△A₂B₂C₂．

　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　

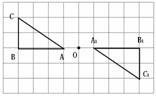
[答案]如图：

20．