
题目列表(包括答案和解析)
10.(2011湖北襄阳,26,13分)
如图10,在平面直角坐标系xOy中,AB在x轴上,AB=10,以AB为直径的⊙O′与y轴正半轴交于点C,连接BC,AC.CD是⊙O′的切线,AD⊥CD于点D,tan∠CAD= ,抛物线
,抛物线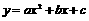 过A,B,C三点.
过A,B,C三点.
(1)求证:∠CAD=∠CAB;
(2)①求抛物线的解析式;
②判定抛物线的顶点E是否在直线CD上,并说明理由;
(3)在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由.


[答案]
(1)证明:连接O′C.
∵CD是⊙O′的切线,∴O′C⊥CD··············· 1分
∵AD⊥CD,∴O′C∥AD,∴∠O′CA=∠CAD··········· 2分
∵O′C=O′A,∴∠O′CA=∠CAB
∴∠CAD=∠CAB.······················· 3分
(2)∵AB是⊙O′的直径,∴∠ACB=90°
∵OC⊥AB,∴∠CAB=∠OCB,∴△CAO∽△BCO,∴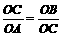
即 ······················ 4分
······················ 4分
∵tan∠CAO=tan∠CAD= ,∴OA=2OC
,∴OA=2OC
又∵AB=10,∴ ∵OC>0
∵OC>0
∴OC=4,OA=8,OB=2.
∴A(-8,0),B(2,0),C(0,4)············· 5分
∵抛物线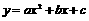 过A,B,C三点.∴c=4
过A,B,C三点.∴c=4
由题意得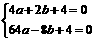 ,解之得
,解之得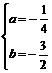 ,
,
∴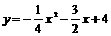 .···················· 7分
.···················· 7分
(3)设直线DC交x轴于点F,易证△AOC≌△ADC,∴AD=AO=8.
∵O′C∥AD,∴△FO′C∽△FAD,∴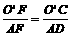
∴8(BF+5)=5(BF+10),∴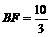 ,∴
,∴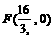 .······ 8分
.······ 8分
设直线DC的解析式为 ,则
,则 ,即
,即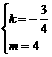
∴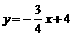 .······················ 9分
.······················ 9分
由 得
得
顶点E的坐标为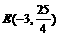 ················· 10分
················· 10分
将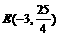 代入直线DC的解析式
代入直线DC的解析式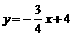 中,
中,
右边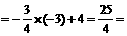 左边.
左边.
∴抛物线的顶点E在直线CD上.··············· 11分
(3)存在.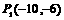 ,
,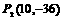 ··············· 13分
··············· 13分
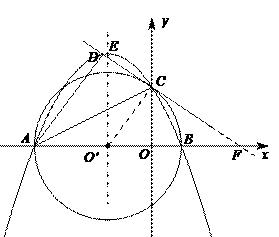
9. (2011湖南衡阳,27,10分)已知抛物线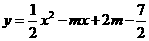 .
.
(1)试说明:无论m为何实数,该抛物线与x轴总有两个不同的交点;
(2)如图,当该抛物线的对称轴为直线x=3时,抛物线的顶点为点C,直线y=x-1与抛物线交于A、B两点,并与它的对称轴交于点D.
①抛物线上是否存在一点P使得四边形ACPD是正方形?若存在,求出点P的坐标;若不存在,说明理由;
②平移直线CD,交直线AB于点M,交抛物线于点N,通过怎样的平移能使得C、D、M、N为顶点的四边形是平行四边形.
[解] (1)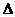 =
=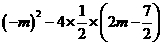 =
=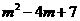 =
=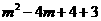 =
= ,∵不管m为何实数,总有
,∵不管m为何实数,总有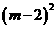 ≥0,∴
≥0,∴ =
= >0,∴无论m为何实数,该抛物线与x轴总有两个不同的交点.
>0,∴无论m为何实数,该抛物线与x轴总有两个不同的交点.
(2)∵ 抛物线的对称轴为直线x=3,∴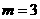 ,
,
抛物线的解析式为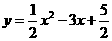 =
= ,顶点C坐标为(3,-2),
,顶点C坐标为(3,-2),
解方程组 ,解得
,解得 或
或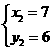 ,所以A的坐标为(1,0)、B的坐标为(7,6),∵
,所以A的坐标为(1,0)、B的坐标为(7,6),∵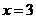 时y=x-1=3-1=2,∴D的坐标为(3,2),设抛物线的对称轴与
时y=x-1=3-1=2,∴D的坐标为(3,2),设抛物线的对称轴与 轴的交点为E,则E的坐标为(3,0),所以AE=BE=3,DE=CE=2,
轴的交点为E,则E的坐标为(3,0),所以AE=BE=3,DE=CE=2,
① 假设抛物线上存在一点P使得四边形ACPD是正方形,则AP、CD互相垂直平分且相等,于是P与点B重合,但AP=6,CD=4,AP≠CD,故抛物线上不存在一点P使得四边形ACPD是正方形.

②
(Ⅰ)设直线CD向右平移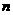 个单位(
个单位(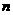 >0)可使得C、D、M、N为顶点的四边形是平行四边形,则直线CD的解析式为x=3
>0)可使得C、D、M、N为顶点的四边形是平行四边形,则直线CD的解析式为x=3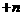 ,直线CD与直线y=x-1交于点M(3
,直线CD与直线y=x-1交于点M(3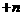 ,2
,2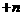 ),又∵D的坐标为(3,2),C坐标为(3,-2),∴D通过向下平移4个单位得到C.
),又∵D的坐标为(3,2),C坐标为(3,-2),∴D通过向下平移4个单位得到C.
∵C、D、M、N为顶点的四边形是平行四边形,∴四边形CDMN是平行四边形或四边形CDNM是平行四边形.
(ⅰ)当四边形CDMN是平行四边形,∴M向下平移4个单位得N,
∴N坐标为(3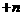 ,
,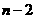 ),
),
又N在抛物线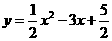 上,∴
上,∴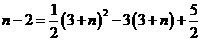 ,
,
解得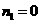 (不合题意,舍去),
(不合题意,舍去), ,
,
(ⅱ)当四边形CDNM是平行四边形,∴M向上平移4个单位得N,
∴N坐标为(3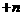 ,
,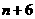 ),
),
又N在抛物线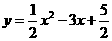 上,∴
上,∴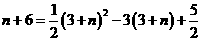 ,
,
解得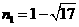 (不合题意,舍去),
(不合题意,舍去), ,
,
(Ⅱ) 设直线CD向左平移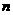 个单位(
个单位(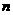 >0)可使得C、D、M、N为顶点的四边形是平行四边形,则直线CD的解析式为x=3
>0)可使得C、D、M、N为顶点的四边形是平行四边形,则直线CD的解析式为x=3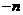 ,直线CD与直线y=x-1交于点M(3
,直线CD与直线y=x-1交于点M(3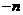 ,2
,2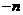 ),又∵D的坐标为(3,2),C坐标为(3,-2),∴D通过向下平移4个单位得到C.
),又∵D的坐标为(3,2),C坐标为(3,-2),∴D通过向下平移4个单位得到C.
∵C、D、M、N为顶点的四边形是平行四边形,∴四边形CDMN是平行四边形或四边形CDNM是平行四边形.
(ⅰ)当四边形CDMN是平行四边形,∴M向下平移4个单位得N,
∴N坐标为(3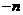 ,
,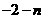 ),
),
又N在抛物线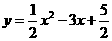 上,∴
上,∴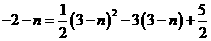 ,
,
解得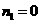 (不合题意,舍去),
(不合题意,舍去), (不合题意,舍去),
(不合题意,舍去),
(ⅱ)当四边形CDNM是平行四边形,∴M向上平移4个单位得N,
∴N坐标为(3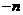 ,
,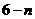 ),
),
又N在抛物线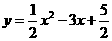 上,∴
上,∴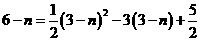 ,
,
解得 ,
,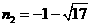 (不合题意,舍去),
(不合题意,舍去),
综上所述,直线CD向右平移2或(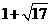 )个单位或向左平移(
)个单位或向左平移(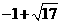 )个单位,可使得C、D、M、N为顶点的四边形是平行四边形.
)个单位,可使得C、D、M、N为顶点的四边形是平行四边形.
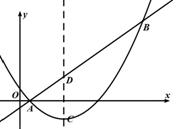
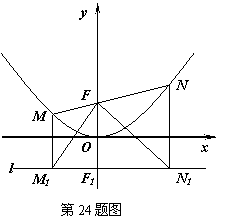
8. (2011湖北黄冈,24,14分)如图所示,过点F(0,1)的直线y=kx+b与抛物线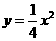 交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
⑴求b的值.
⑵求x1•x2的值
⑶分别过M、N作直线l:y=-1的垂线,垂足分别是M1、N1,判断△M1FN1的形状,并证明你的结论.
⑷对于过点F的任意直线MN,是否存在一条定直线m,使m与以MN为直径的圆相切.如果有,请法度出这条直线m的解析式;如果没有,请说明理由.

[答案]解:⑴b=1
⑵显然 和
和 是方程组
是方程组 的两组解,解方程组消元得
的两组解,解方程组消元得 ,依据“根与系数关系”得
,依据“根与系数关系”得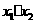 =-4
=-4


⑶△M1FN1是直角三角形是直角三角形,理由如下:
由题知M1的横坐标为x1,N1的横坐标为x2,设M1N1交y轴于F1,则F1M1•F1N1=-x1•x2=4,而FF1=2,所以F1M1•F1N1=F1F2,另有∠M1F1F=∠FF1N1=90°,易证Rt△M1FF1∽Rt△N1FF1,得∠M1FF1=∠FN1F1,故∠M1FN1=∠M1FF1+∠F1FN1=∠FN1F1+∠F1FN1=90°,所以△M1FN1是直角三角形.
⑷存在,该直线为y=-1.理由如下:
直线y=-1即为直线M1N1.
如图,设N点横坐标为m,则N点纵坐标为 ,计算知NN1=
,计算知NN1= , NF=
, NF=
 ,得NN1=NF
,得NN1=NF
同理MM1=MF.
那么MN=MM1+NN1,作梯形MM1N1N的中位线PQ,由中位线性质知PQ=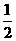 (MM1+NN1)=
(MM1+NN1)=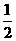 MN,即圆心到直线y=-1的距离等于圆的半径,所以y=-1总与该圆相切.
MN,即圆心到直线y=-1的距离等于圆的半径,所以y=-1总与该圆相切.
7. (2011四川乐山26,13分)已知顶点为A(1,5)的抛物线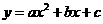 经过点B(5,1).
经过点B(5,1).
(1)求抛物线的解析式;
(2)如图(15.1),设C,D分别是x轴、y轴上的两个动点,求四边形ABCD周长的最小值
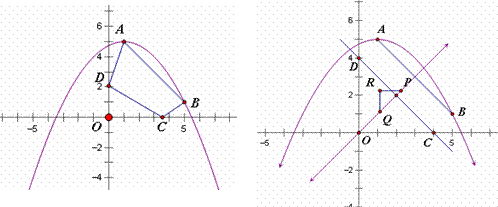
(3)在(2)中,当四边形ABCD的周长最小时,作直线CD.设点P(x,y)(x>0)是直线y=x上的一个动点,Q是OP的中点,以PQ为斜边按图(15.2)所示构造等腰直角三角形PRQ.
①当△PBR与直线CD有公共点时,求x的取值范围;
②在①的条件下,记△PBR与△COD的公共部分的面积为S.求S关于x的函数关系式,并求S的最大值。
[答案]
解:⑴.设以A(1,5)为顶点的二次函数解析式为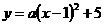
∵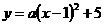 的图像经过了点B(5,5)
的图像经过了点B(5,5)
∴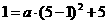 解得
解得
∴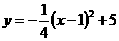
即: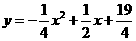
⑵.
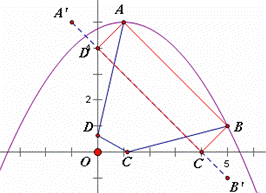
如图,作点A关于y轴对称点 ,与y轴交与点D,作点B关于x轴对称点
,与y轴交与点D,作点B关于x轴对称点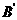 ,与x轴交与点C,连接AD,AC,CB,BA.四边形ABCD的周长最小。
,与x轴交与点C,连接AD,AC,CB,BA.四边形ABCD的周长最小。
∵A(1,5),B(5,1)
∴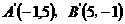
∴

⑶.①如图
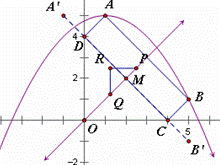
∵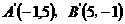
∴直线AB的解析式为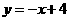
∴直线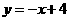 与直线
与直线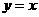 的交点
的交点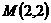
∵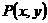 ,点Q为OP的中点
,点Q为OP的中点
∴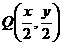
∵△PBR与直线CD有公共点,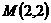
∴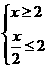 ,即
,即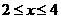
6. (2011上海,24,12分)已知平面直角坐标系xOy(如图),一次函数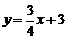 的图像与y轴交于点A,点M在正比例函数
的图像与y轴交于点A,点M在正比例函数 的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
的图像上,且MO=MA.二次函数y=x2+bx+c的图像经过点A、M.
(1)求线段AM的长;
(2)求这个二次函数的解析式;
(3)如果点B在y轴上,且位于点A下方,点C在上述二次函数的图像上,点D在一次函数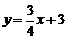 的图像上,且四边形ABCD是菱形,求点C的坐标.
的图像上,且四边形ABCD是菱形,求点C的坐标.
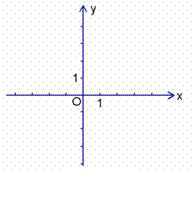

[答案](1)一次函数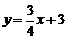 ,当x=0时,y=3.所以点A的坐标为(0,3).
,当x=0时,y=3.所以点A的坐标为(0,3).
正比例函数 ,当y
=
,当y
=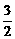 时,x=1.所以点M的坐标为(1,
时,x=1.所以点M的坐标为(1,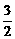 ).
).
如下图,AM=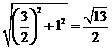 .
.

(2)将点A(0,3)、M(1,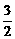 )代入y=x2+bx+c中,得
)代入y=x2+bx+c中,得
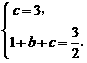
解得
即这个二次函数的解析式为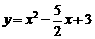 .
.
(3)

设B(0,m)(m<3),C(n,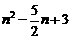 ),D(n,
),D(n,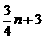 ).则
).则
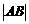 =
=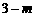 ,
,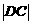 =
=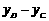 =
=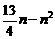 ,
,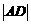 =
= .
.
因为四边形ABCD是菱形,所以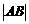 =
=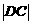 =
=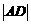 .
.
所以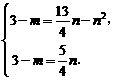
解得 (舍去)
(舍去)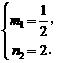
将n=2代入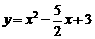 ,得
,得 =2.所以点C的坐标为(2,2).
=2.所以点C的坐标为(2,2).
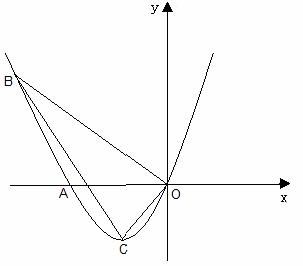
5. (2011山东临沂,26,13分)如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P使得以点P、M、A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
解:(1)∵抛物线过原点O,
∴可设抛物线的解析式为y=ax2+bx,
将A(-2,0),B(-3,3)代入,得
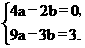
解得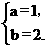
∴此抛物线的解析式为y=x2+2x.……………………(3分)
(2)如图,①当AO为边时,
∵以A、O、D、E为顶点的四边形是平行四边形,
∴DE∥AO,且DE=AO=2,…………………………………………( 4分)
点E在对称轴x=-1上,
∴点D的横坐标为1或-3,…………………………………………( 5分)
即符合条件的点D有两个,分别记为:D1,D2,
而当x=1时,y=3;当x=-3时,y=3,
∴D1(1,3),D2(-3,3).…………………………………………(7分)
②当AO为对角线时,则DE与AO互相平分,
又点E在对称轴上,
且线段AO的中点横坐标为-1,
由对称性知,符合条件的点D只有一个,即顶点C(-1,,1),
综上所述,符合条件的点D共有三个,分别为D1(1,3),D2(-3,3),C(-1,,1).………………………………………………………(8分)

③存在.…………………………………………………………………(9分)
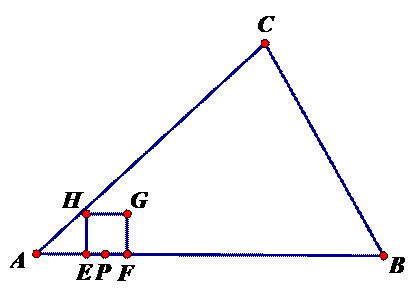
4. (2011江苏淮安,28,12分)如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立即以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
(1)当t=1时,正方形EFGH的边长是 ;当t=3时,正方形EFGH的边长是 ;
(2)当0<t≤2时,求S与t的函数关系式;
(3)直接答出:在整个运动过程中,当t为何值时,S最大?最大面积是多少?
[答案](1)2;6;
(2) 当0<t≤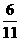 时(如图),求S与t的函数关系式是:S=
时(如图),求S与t的函数关系式是:S= =(2t)2=4t2;
=(2t)2=4t2;

当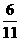 <t≤
<t≤ 时(如图),求S与t的函数关系式是:S=
时(如图),求S与t的函数关系式是:S= -S△HMN=4t2-
-S△HMN=4t2-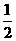 ×
× ×[2t-
×[2t-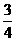 (2-t)] 2
=
(2-t)] 2
= t2+
t2+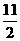 t-
t-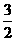 ;
;

当 <t≤2时(如图),求S与t的函数关系式是:S= S△ARF
-S△AQE =
<t≤2时(如图),求S与t的函数关系式是:S= S△ARF
-S△AQE =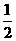 ×
×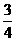 (2+t) 2 -
(2+t) 2 -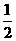 ×
×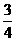 (2-t) 2=3t.
(2-t) 2=3t.

(3)由(2)知:若0<t≤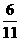 ,则当t=
,则当t=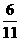 时S最大,其最大值S=
时S最大,其最大值S= ;
;
若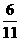 <t≤
<t≤ ,则当t=
,则当t= 时S最大,其最大值S=
时S最大,其最大值S= ;
;
若 <t≤2,则当t=2时S最大,其最大值S=6.
<t≤2,则当t=2时S最大,其最大值S=6.
综上所述,当t=2时S最大,最大面积是6.
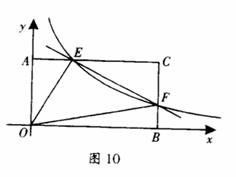
3. (2011湖南怀化,24,10分)在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B,C重合),过F点的反比例函数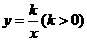 的图像与AC边交于点E.
的图像与AC边交于点E.
(1) 求证:AE×AO=BF×BO;
(2) 若点E的坐标为(2,4),求经过O、E、F三点的抛物线的解析式;
(3) 是否存在这样的点F,使得将△CEF沿EF对折后,C点恰好落在OB上?若存在,求出此时的OF长;若不存在,请说明理由.
[答案]
(1)证明:由题意知,点E、F均在反比例函数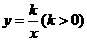 图像上,且在第一象限,所以AE×AO=k,BF×BO=k,从而AE×AO=BF×BO.
图像上,且在第一象限,所以AE×AO=k,BF×BO=k,从而AE×AO=BF×BO.
(2)将点E的坐标为(2,4)代入反比例函数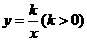 得k=8,
得k=8,
所以反比例函数的解析式为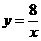 .
.
∵OB=6,∴当x=6时,y=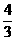 ,点F的坐标为(6,
,点F的坐标为(6,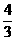 ).
).
设过点O、E、F三点的二次函数表达式为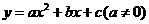 ,将点O(0,0),E(2、4),F(6,
,将点O(0,0),E(2、4),F(6,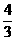 )三点的坐标代入表达式得:
)三点的坐标代入表达式得:
 解得
解得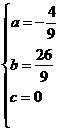
∴经过O、E、F三点的抛物线的解析式为: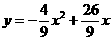 .
.
(1) 如图11,将△CEF沿EF对折后,C点恰好落在OB边于点C′.过点E作EH⊥OB于点H.

设CE=n,CF=m,则AE=6-n,BF=4-m
由(1)得AE×AO=BF×BO ∴(6-n)×4=(4-m)×6 ,解得n=1.5m.
由折叠可知,CF=C′F=m,CE=C′E=1.5m,∠EC′F=∠C=90°
在Rt△EHC′中,∠EC′H+∠C′EH=90°,
又∵∠EC′H+∠EC′F+FC′B=180°,∠EC′F=90°
∴∠C′EH=FC′B
∵∠EHC′=C′BF=90°
∴△EC′H∽△C′FB,∴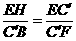
∴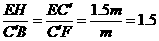 ,
,
∵由四边形AEHO为矩形可得EH=AO=4 ∴C′B=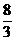 .
.
在Rt△BC′F中,由勾股定理得,C′F2=BF2+C′B2,即m2=(4-m)2+
解得:m=
BF=4- =
=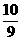 ,
,
在Rt△BOF中,由勾股定理得,OF2=BF2+OB2,即OF2=62+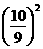 =
=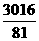 .
.
∴OF=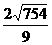
∴存在这样的点F,OF=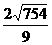 ,使得将△CEF沿EF对折后,C点恰好落在OB上.
,使得将△CEF沿EF对折后,C点恰好落在OB上.
2. (2011广东省,22,9分)如图,抛物线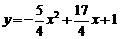 与y轴交于点A,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与y轴交于点A,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
(1)求直线AB的函数关系式;
(2)动点P在线段OC上,从原点O出发以每钞一个单位的速度向C移动,过点P作⊥x轴,交直线AB于点M,抛物线于点N,设点P移动的时间为t秒,MN的长为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)设(2)的条件下(不考虑点P与点O,点G重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平等四边形?问对于所求的t的值,平行四边形BCMN是否为菱形?说明理由.

[解](1)把x=0代入 ,得
,得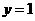
把x=3代入 ,得
,得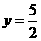 ,
,
∴A、B两点的坐标分别(0,1)、(3, )
)
设直线AB的解析式为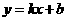 ,代入A、B的坐标,得
,代入A、B的坐标,得
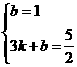 ,解得
,解得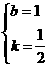
所以,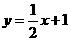
(2)把x=t分别代入到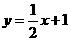 和
和
分别得到点M、N的纵坐标为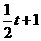 和
和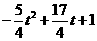
∴MN=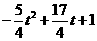 -(
-(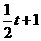 )=
)=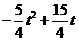
即
∵点P在线段OC上移动,
∴0≤t≤3.
(3)在四边形BCMN中,∵BC∥MN
∴当BC=MN时,四边形BCMN即为平行四边形
由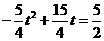 ,得
,得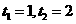
即当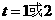 时,四边形BCMN为平行四边形
时,四边形BCMN为平行四边形
当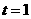 时,PC=2,PM=
时,PC=2,PM=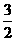 ,PN=4,由勾股定理求得CM=BN=
,PN=4,由勾股定理求得CM=BN= ,
,
此时BC=CM=MN=BN,平行四边形BCMN为菱形;
当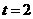 时,PC=1,PM=2,由勾股定理求得CM=
时,PC=1,PM=2,由勾股定理求得CM=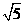 ,
,
此时BC≠CM,平行四边形BCMN不是菱形;
所以,当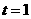 时,平行四边形BCMN为菱形.
时,平行四边形BCMN为菱形.
1. (2011重庆綦江,26,12分)在如图的直角坐标系中,已知点A(1,0);B(0,-2),将线段AB绕点A按逆时针方向旋转90°至AC.
⑴ 求点C的坐标;
⑵ 若抛物线 经过点C.
经过点C.
①求抛物线的解析式;
②在抛物线上是否存在点P(点C除外)使△ABP是以AB为直角边的等腰直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
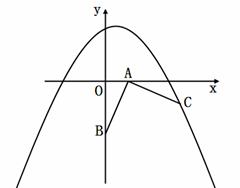
[答案]:解:(1)过点C作CD⊥x轴,垂足为D,
在△ACD和△BAO中,由已知有∠CAD+∠BAO=90°,而∠ABO+∠BAO=90°∴∠CAD=∠ABO,又∵∠CAD=∠AOB=90°,且由已知有CA=AB,∴△ACD≌△BAO,∴CD=OA=1,AD=BO=2,∴点C的坐标为(3,-1)
(2)①∵抛物线 经过点C(3,-1),∴
经过点C(3,-1),∴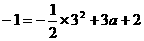 ,解得
,解得
∴抛物线的解析式为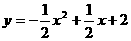
解法一:② i) 当A为直角顶点时 ,延长CA至点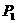 ,使
,使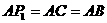 ,则△
,则△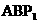 是以AB为直角边的等腰直角三角形,
是以AB为直角边的等腰直角三角形,
如果点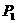 在抛物线上,则
在抛物线上,则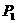 满足条件,过点
满足条件,过点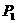 作
作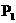
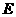 ⊥
⊥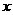 轴, ∵
轴, ∵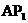 =
= ,∠
,∠ =∠
=∠ ,∠
,∠ =∠
=∠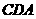 =90°, ∴△
=90°, ∴△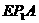 ≌△
≌△ ,∴AE=AD=2,
,∴AE=AD=2,  =CD=1,
=CD=1,
∴可求得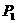 的坐标为(-1,1),经检验
的坐标为(-1,1),经检验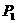 点在抛物线上,因此存在点
点在抛物线上,因此存在点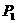 满足条件;
满足条件;
ii) 当B点为直角顶点时,
过点B作直线L⊥BA,在直线L上分别取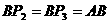 ,得到以AB为直角边的等腰直角△
,得到以AB为直角边的等腰直角△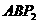 和等腰直角△
和等腰直角△ ,作
,作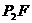 ⊥y轴,同理可证△
⊥y轴,同理可证△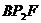 ≌△
≌△
∴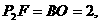 BF=OA=1,可得点
BF=OA=1,可得点 的坐标为(-2,-1),经检验
的坐标为(-2,-1),经检验 点在抛物线上,因此存在点
点在抛物线上,因此存在点 满足条件.同理可得点
满足条件.同理可得点 的坐标为(2,-3),经检验
的坐标为(2,-3),经检验 点不在抛物线上.
点不在抛物线上.
综上:抛物线上存在点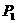 (-1,1),
(-1,1), (-2,-1)两点,使得△
(-2,-1)两点,使得△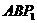 和△
和△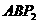
是以AB为直角边的等腰直角三角形.
解法二:(2)②(如果有用下面解法的考生可以给满分)
i) 当点A为直角顶点时,易求出直线AC的解析式为
由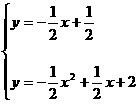 解之可得
解之可得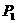 (-1,1) (已知点C除外)作
(-1,1) (已知点C除外)作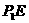 ⊥x轴于E,则AE=2,
⊥x轴于E,则AE=2, 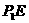 =1, 由勾股定理有又∵AB=
=1, 由勾股定理有又∵AB= ,∴
,∴ ,∴△
,∴△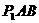 是以AB为直角边的等腰三角形;
是以AB为直角边的等腰三角形;
ii)当B点为直角顶点时,过B作直线L∥AC交抛物线于点 和点
和点 ,易求出直线L的解析式为
,易求出直线L的解析式为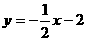 ,由
,由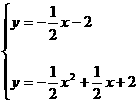 解得
解得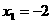 或
或
∴ (-2,-1),
(-2,-1), (4,-4)作
(4,-4)作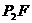 ⊥y轴于F,同理可求得
⊥y轴于F,同理可求得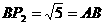
∴△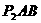 是以AB为直角边的等腰三角形作
是以AB为直角边的等腰三角形作 ⊥y轴于H,可求得
⊥y轴于H,可求得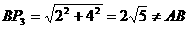 ,∴Rt△
,∴Rt△ 不是等腰直角三角形,∴点
不是等腰直角三角形,∴点 不满足条件.
不满足条件.
综上:抛物线上存在点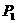 (-1,1),
(-1,1), (-2,-1)两点,使得△
(-2,-1)两点,使得△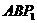 和△
和△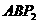 是以角AB为直边的等腰直角三角形.
是以角AB为直边的等腰直角三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com