
题目列表(包括答案和解析)
3. (2011山东潍坊,22,10分)2011年上半年,某种农产品受不良炒作的影响,价格一路上扬,8月初国家实施调控措施后,该农产品的价格开始回落.其中,1月份至7月份,该农产品的月平均价格y元/千克与月份x呈一次函数关系;7月份至12月份,月平均价格元/千克与月份x呈二次函数关系.已知1月、7月、9月和12月这四个月的月平均价格分别为8元/千克、26元/千克、14元/千克、11元/千克.
(1)分别求出当1≤x≤7和7≤x≤12时,y关于x的函数关系式;
(2)2011年的12个月中,这种农产品的月平均价格哪个月最低?最低为多少?
(3)若以12个月份的月平均价格的平均数为年平均价格,月平均价格高于年平均价格的月份有哪些?
[解](1)当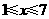 时,设
时,设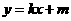 ,
,
将点(1,8)、(7,26)分别代入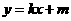 ,得
,得
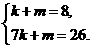 解之,得
解之,得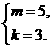
∴函数解析式为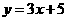 .
.
当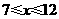 时,设
时,设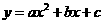 ,
,
将(7,26)、(9,14)、(12,11)分别代入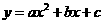 ,得:
,得:
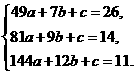 解之,得
解之,得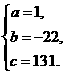
∴函数解析式为 .
.
(2)当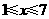 时,函数
时,函数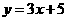 中y随x的增大而增大,
中y随x的增大而增大,
∴当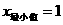 时,
时,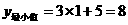 .
.
当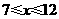 时,
时, ,
,
∴当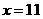 时,
时,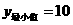 .
.
所以,该农产品平均价格最低的是1月,最低为8元/千克.
(3)∵1至7月份的月平均价格呈一次函数,
∴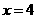 时的月平均价格17是前7个月的平均值.
时的月平均价格17是前7个月的平均值.
将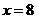 ,
,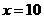 和
和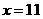 分别代入
分别代入 ,得
,得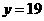 ,
,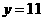 和
和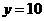 .
.
∴后5个月的月平均价格分别为19,14,11,10,11.
∴年平均价格为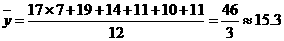 (元/千克).
(元/千克).
当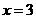 时,
时,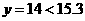 ,
,
∴4,5,6,7,8这五个月的月平均价格高于年平均价格.
2. (2011四川重庆,25,10分)某企业为重庆计算机产业基地提供电脑配件.受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
|
月份x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
价格y1(元/件) |
560 |
580 |
600 |
620 |
640 |
660 |
680 |
700 |
720 |
随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:
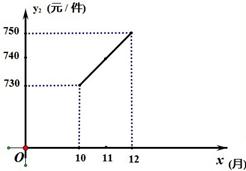
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1 与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;
(2)若去年该配件每件的售价为1000元,生产每件配件的人力成本为50元,其它成本30元,该配件在1至9月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤9,且x取整数),10至12月的销售量p2(万件)p2=-0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润;
(3)今年1至5月,每件配件的原材料价格均比去年12月上涨60元,人力成本比去年增加20%,其它成本没有变化,该企业将每件配件的售价在去年的基础上提高a%,与此同时每月销售量均在去年12月的基础上减少0.1 a%.这样,在保证每月上万件配件销量的前提下,完成1至5月的总利润1700万元的任务,请你参考以下数据,估算出a的整数值.(参考数据:992=9801,982=9604,972=9409,962=9216,952=9025)
[答案](1)y1 与x之间的函数关系式为y1=20x+540,
y2与x之间满足的一次函数关系式为y2=10x+630.
(2)去年1至9月时,销售该配件的利润w= p1(1000-50-30-y1)
=(0.1x+1.1)(1000−50−30−20x−540)
=(0.1x+1.1)(380−20x)=-2x2+160x+418
=-2( x-4)2+450,(1≤x≤9,且x取整数)
∵-2<0,1≤x≤9,∴当x=4时,w最大=450(万元);
去年10至12月时,销售该配件的利润w= p2(1000-50-30-y2)
=(-0.1x+2.9)(1000-50-30-10x-630)
=(-0.1x+2.9)(290-10x)=( x-29)2,(10≤x≤12,且x取整数),
当10≤x≤12时,∵x<29,∴自变量x增大,函数值w减小,
∴当x=10时,w最大=361(万元),∵450>361,
∴去年4月销售该配件的利润最大,最大利润为450万元.
(3)去年12月份销售量为:-0.1×12+0.9=1.7(万件),
今年原材料的价格为:750+60=810(元),
今年人力成本为:50×(1+20﹪)=60(元),
由题意,得5×[1000(1+a﹪)-810-60-30]×1.7(1-0.1a﹪)=1700,
设t= a﹪,整理,得10t2-99t+10=0,解得t=,∵972=9409,962=9216,而9401更接近9409.∴=97.
∴t1≈0.1或t2≈9.8,∴a1≈10或a2≈980.
∵1.7(1-0.1a﹪)≥1,∴a2≈980舍去,∴a≈10.
答:a的整数值为10.
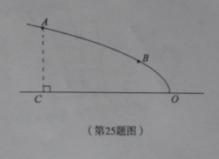
1. (2011山东滨州,25,12分)如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O落在水平面上,对称轴是水平线OC。点A、B在抛物线造型上,且点A到水平面的距离AC=4O米,点B到水平面距离为2米,OC=8米。
(1) 请建立适当的直角坐标系,求抛物线的函数解析式;
(2) 为了安全美观,现需在水平线OC上找一点P,用质地、规格已确定的圆形钢管制作两根支柱PA、PB对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省(支柱与地面、造型对接方式的用料多少问题暂不考虑)时的点P?(无需证明)
(3) 为了施工方便,现需计算出点O、P之间的距离,那么两根支柱用料最省时点O、P之间的距离是多少?(请写出求解过程)
[答案]
解:(1)以点O为原点、射线OC为y轴的正半轴建立直角坐标系………………1分
设抛物线的函数解析式为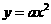 ,………………2分
,………………2分
由题意知点A的坐标为(4,8)。且点A在抛物线上,………………3分
所以8=a×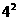 ,解得a=
,解得a=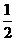 ,故所求抛物线的函数解析式为
,故所求抛物线的函数解析式为 ………………4分
………………4分
(2)找法:延长AC,交建筑物造型所在抛物线于点D, ………………5分
则点A、D关于OC对称。
连接BD交OC于点P,则点P即为所求。………………6分
(3)由题意知点B的横坐标为2,且点B在抛物线上,
所以点B的坐标为(2,2)………………7分
又知点A的坐标为(4,8),所以点D的坐标为(-4,8)………………8
设直线BD的函数解析式为 y=kx+b,………………9
则有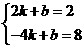 ………………10
………………10
解得k=-1,b=4.
故直线BD的函数解析式为 y=-x+4,………………11
把x=0代入 y=-x+4,得点P的坐标为(0,4)
两根支柱用料最省时,点O、P之间的距离是4米。………………12
5.
4.
3.
2. (2011江苏扬州,17,3分)如图,已知函数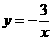 与
与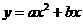 (a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程
(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程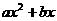
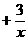 =0的解为
=0的解为
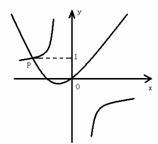
[答案]-3
1. (2011湖南怀化,16,3分)出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,则当x=________元时,一天出售该种手工艺品的总利润y最大.
[答案]4
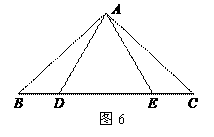
4. (2011湖北襄阳,21,6分)
如图6,点D,E在△ABC的边BC上,连接AD,AE. ①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①② ③;①③
③;①③ ②;②③
②;②③ ①.
①.
(1)以上三个命题是真命题的为(直接作答) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).

[答案](1)①② ③;①③
③;①③ ②;②③
②;②③ ①.········· 3分
①.········· 3分
(2)(略) 6分
4. (2011山东烟台,24,10分)已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
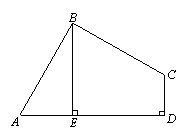 (2)当BE⊥AD于E时,试证明:BE=AE+CD.
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
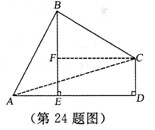 [答案](1)证明:连接AC,
[答案](1)证明:连接AC,
∵∠ABC=90°,
∴AB2+BC2=AC2.
∵CD⊥AD,∴AD2+CD2=AC2.
∵AD2+CD2=2AB2,∴AB2+BC2=2AB2,
∴AB=BC.
(2)证明:过C作CF⊥BE于F.
∵BE⊥AD,∴四边形CDEF是矩形.
∴CD=EF.
∵∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,∴△BAE≌△CBF.
∴AE=BF.
∴BE=BF+EF =AE+CD.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com