
题目列表(包括答案和解析)
24. (2011江苏连云港,25,10分)如图,抛物线 与x轴交于A,B两点,与y轴交于点C,其顶点在直线y=-2x上.
与x轴交于A,B两点,与y轴交于点C,其顶点在直线y=-2x上.
(1)求a的值;
(2)求A,B两点的坐标;
(3)以AC,CB为一组邻边作□ABCD,则点D关于x轴的对称点D´是否在该抛物线上?请说明理由.

[答案]解:(1)∵二抛物线 的顶点坐标为
的顶点坐标为 ,∴x=1,∵顶点在直线y=-2x上,所以y=-2,即顶点坐标为(1,-2),∴-2=
,∴x=1,∵顶点在直线y=-2x上,所以y=-2,即顶点坐标为(1,-2),∴-2= -1+a,即a=-
-1+a,即a=- 4;(2)二次函数的关系式为
4;(2)二次函数的关系式为 ,当y=0时,
,当y=0时,
 ,解之得:
,解之得: ,即A(-1,0),B(3,0);(3)如图所示:直线BD//AC,AD//BC,因为A(-1.0),C(0,
,即A(-1,0),B(3,0);(3)如图所示:直线BD//AC,AD//BC,因为A(-1.0),C(0, ),所以直线AB的解析式为
),所以直线AB的解析式为 ,所以设BD的解析式为
,所以设BD的解析式为 ,因为B(3,0),所以b=
,因为B(3,0),所以b= ,直线BD的解析式为:
,直线BD的解析式为: ,同理可得:直线AD的解析式为:
,同理可得:直线AD的解析式为: ,因此直线BD与CD的交点坐标为:(2,
,因此直线BD与CD的交点坐标为:(2, ),则点D关于x轴的对称点D´是(2,-
),则点D关于x轴的对称点D´是(2,- ),当x=2时代入
),当x=2时代入 得,y=
得,y= ,所以D´在二次函数
,所以D´在二次函数 的图象上.
的图象上.

23. (2011广东株洲,24,10分)孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线 的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点O,两直角边与该抛物线交于A、B两点,请解答以下问题:
的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点O,两直角边与该抛物线交于A、B两点,请解答以下问题:
(1)若测得 (如图1),求
(如图1),求 的值;
的值;
(2)对同一条抛物线,孔明将三角板绕点O旋转到如图2所示位置时,过B作BF⊥x轴于点F,测得OF=1,写出此时点B的坐标,并求点A的横坐标;
(3)对该抛物线,孔明将三角板绕点O旋转任意角度时惊奇地发现,交点A、B的连线段总经过一个固定的点,试说明理由并求出该点的坐标.

[答案]解:(1)设线段AB与y轴的交点为C,由抛物线的对称性可得C为AB中点,
∵  ,∠AOB=90°,
,∠AOB=90°,
∴AC=OC=BC=2,∴B(2,-2),
将B(2,-2)代入抛物线 得,
得, .
.
(2)解法一:过点A作AE⊥x轴于点E,
∵点B的横坐标为1,∴B (1, ),
),
∴ . 又∵∠AOB=90°,易知∠AOE=∠OBF,又∠AEO=∠OFB=90°,
. 又∵∠AOB=90°,易知∠AOE=∠OBF,又∠AEO=∠OFB=90°,
∴△AEO∽△OFB,∴ ∴AE=2OE,
∴AE=2OE,
设点A( ,
, )(m>0),则OE=m,
)(m>0),则OE=m, ,∴
,∴
∴m=4,即点A的横坐标为-4.
解法二:过点A作AE⊥x轴于点E,
∵点B的横坐标为1,∴B (1, ),
),
∴
∵∠AOB=90°,易知∠AOE=∠OBF,
∴ ,∴AE=2OE,
,∴AE=2OE,
设点A(- ,
, )(m>0),则OE=m,
)(m>0),则OE=m, ,∴
,∴
∴m=4,即点A的横坐标为-4.
解法三:过点A作AE⊥x轴于点E,
∵点B的横坐标为1,∴B (1, ),
),
设A(- ,
, )(m>0),则
)(m>0),则
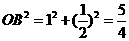 ,
, ,
, ,
,
∵∠AOB=90°,∴ ,
,
∴ ,
,
解得:m=4,即点A的横坐标为-4.
(3)解法一:设A( ,
, )(m>0),B(
)(m>0),B( ,
, )(n>0),
)(n>0),
设直线AB的解析式为:y=kx+b, 则 ,
,
(1)×n+(2)×m得, ,
,
∴
又易知△AEO∽△OFB,∴ ,∴
,∴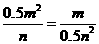 ,∴mn=4,
,∴mn=4,
∴ .由此可知不论k为何值,直线AB恒过点(0,-2),
.由此可知不论k为何值,直线AB恒过点(0,-2),
(说明:写出定点C的坐标就给2分)
解法二:设A( ,
, )(m>0),B(
)(m>0),B( ,
, )(n>0),
)(n>0),
直线AB与y轴的交点为C,根据 ,可得
,可得
 ,
,
化简,得 .
.
又易知△AEO∽△OFB,∴ ,∴
,∴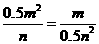 ,∴mn=4,∴OC=2为固定值.故直线AB恒过其与y轴的交点C(0,-2)
,∴mn=4,∴OC=2为固定值.故直线AB恒过其与y轴的交点C(0,-2)
说明:mn的值也可以通过以下方法求得.
由前可知, ,
, ,
,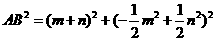 ,
,
由 ,得:
,得: ,
,
化简,得mn=4.
22.(2011湖南益阳,20,10分)如图9,已知抛物线经过定点A(1,0),它的顶点P是y轴正半轴上的一个动点,P点关于x轴的对称点为P′,过P′ 作x轴的平行线交抛物线于B、D两点(B点在y轴右侧),直线BA交y轴于C点.按从特殊到一般的规律探究线段CA与CB的比值:
(1)当P点坐标为(0,1)时,写出抛物线的解析式并求线段CA与CB的比值;
(2)若P点坐标为(0,m)时(m为任意正实数),线段CA与CB的比值是否与⑴所求的比值相同?请说明理由.


[答案]解:⑴ 设抛物线的解析式为 ,
,
 抛物线经过
抛物线经过 ,
, ,
,
 .
.
 ,
,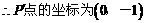
 ∥
∥ ,
, ,
,
由 ,
,
 ,
, .
.
 ,
, ∽
∽ ,
,
 .
.
⑵ 设抛物线的解析式为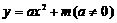
 ,
,
 .
.
 ∥
∥
 ,
, 
 ,
, ,
, ,
, ,
,
 ,
, ,
,
同⑴得
 .
.
21. (2011甘肃兰州,28,12分)如图所示,在平面直角坐标系xoy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线 经过点A、B和D(4,
经过点A、B和D(4, )。
)。
(1)求抛物线的表达式。
(2)如果点P由点A出发沿AB边以2cm/s的速度向点B运动,同时点Q由点B出发,沿BC边以1cm/s
的速度向点C运动,当其中一点到达终点时,另一点也随之停止运动。设S=PQ2(cm2)。
①试求出S与运动时间t之间的函数关系式,并写出t的取值范围;
②当S取 时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由。
时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由。
(3)在抛物线的对称轴上求点M,使得M到D、A的距离之差最大,求出点M的坐标。


[答案](1)由题意得A(0,-2),B(2,-2),抛物线 过A、B、D三点得
过A、B、D三点得
 解得
解得
抛物线的表达式为
(2)①S=PQ2= (0≤t≤1)
(0≤t≤1)
②由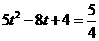 解得t=
解得t= 或t=
或t= (不合题意,舍去)
(不合题意,舍去)
此时,P(1,-2),B(2,-2),Q(2, )
)
若以点P、B、Q、R为顶点的四边形是平行四边形,则R(3, )或(1,-
)或(1,- )或(1,
)或(1, )
)
经代入抛物线表达式检验,只有点R(3, )在抛物线上
)在抛物线上
所以抛物线上存在点R(3, )使得以点P、B、Q、R为顶点的四边形是平行四边形。
)使得以点P、B、Q、R为顶点的四边形是平行四边形。
(3)过B、D的直线交抛物线对称轴于点M,则该点即为所求。因为如在对称轴上另取一点N,则
ND-NA=ND-NB<BD,而MD-MA=MD-MB=BD,故点M到D、A的距离之差最大。
由B(2,-2)、D(4, )求得直线BD的解析式为
)求得直线BD的解析式为
 时,
时, ,故点M的坐标为(1,
,故点M的坐标为(1,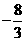 )
)


20. (2011江西,24,10分)将抛物线c1:y=- x2+
x2+ 沿x轴翻折,得抛物线c2,如图所示.
沿x轴翻折,得抛物线c2,如图所示.
(1)请直接写出抛物线c2的表达式.
(2)现将抛物线c1向左平移m个单位长度,平移后得的新抛物线的顶点为M,与x轴的交点从左到右依次为A,B;将抛物线c2向右也平移m个单位长度,平移后得到的新抛物线的顶点为N,与x轴交点从左到右依次为D,E.
①当B,D是线段AE的三等分点时,求m的值;
②在平移过程中,是否存在以点A,N,E,M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.

[答案]
[答案]解:(1)y= x2-
x2- .
.
(2)①令- x2+
x2+ =0,得x1=-1,x2=1,则抛物线c1与x轴的两个交点坐标为(-1,0),(1,0).∴A(-1-m,0),B(1+m,0).
=0,得x1=-1,x2=1,则抛物线c1与x轴的两个交点坐标为(-1,0),(1,0).∴A(-1-m,0),B(1+m,0).
当AD= AE时,如图①,(-1+m)-(-1-m)=
AE时,如图①,(-1+m)-(-1-m)= [(1+m)-(-1-m)], ∴m=
[(1+m)-(-1-m)], ∴m=
当AB= AE时,如图②,(1-m)-(-1-m)=
AE时,如图②,(1-m)-(-1-m)= [(1+m)-(-1-m)], ∴m=2.
[(1+m)-(-1-m)], ∴m=2.

∴当m= 或2时,B,D是线段AE的三等分点.
或2时,B,D是线段AE的三等分点.
②存在.理由:连接AN、NE、EM、MA.依题意可得:M(-m,- ).即M,N关于原点O对称,∴OM=ON.∵A(-1-m,0),E(1+m,0),∴A,E关于原点O对称,∴OA=OE,∴四边形ANEM为平行四边形.要使平行四边形ANEM为矩形,必需满足OM=OA,即m2+(
).即M,N关于原点O对称,∴OM=ON.∵A(-1-m,0),E(1+m,0),∴A,E关于原点O对称,∴OA=OE,∴四边形ANEM为平行四边形.要使平行四边形ANEM为矩形,必需满足OM=OA,即m2+( )2=[-(-1-m)]2, ∴m=1.
)2=[-(-1-m)]2, ∴m=1.
∴当m=1时,以点A,N,E,M为顶点的四边形是矩形.
19. (2011浙江丽水,23,10分)在平面直角坐标系中,如图1,将n个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax2+bx+c(a<0)过矩形顶点B、C.
(1)当n=1时,如果a=-1,试求b的值;
(2)当n=2时,如图2,在矩形OABC上方作一边长为1的正方形EFMN,使EF在线段CB上,如果M,N两点也在抛物线上,求出此时抛物线的解析式;
(3)将矩形OABC绕点O顺时针旋转,使得点B落到x轴的正半轴上,如果该抛物线同时经过原点O,
①试求出当n=3时a的值;
②直接写出a关于n的关系式.


[解](1)由题意可知,抛物线对称轴为直线x=,
∴-=,得b=1;

(2)设所求抛物线的解析式为y=ax2+bx+1,
由对称性可知抛物线经过点B(2,1)和点M(,2),
∴解得
∴所求抛物线解析式为y=-x2+ x+1;

(3)①当n=3时,OC=1,BC=3,
设所求抛物线的解析式为y=ax2+bx,
过C作CD⊥OB于点D,则Rt△OCD∽Rt△CBD,
∴==,
设OD=t,则CD=3t,
∵OD2+CD2=OC2,
∴(3t)2+ t 2=12,∴ t==,
∴C(,),又B(,0),
∴把B、C坐标代入抛物线解析式,得
解得:a=-;
②a=-.

18. (2011浙江温州,22,10分)如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连结OA.
(1)求△OAB的面积;
(2)若抛物线 经过点A.
经过点A.
①求c的值;
②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可).

[答案] 解:(1) ∵点A的坐标是(-2,4),AB⊥y轴,
∴AB=2,OB=4,
∴
(2)①把点A的坐标(-2,4)代入 ,
,
得 ,∴c=4
,∴c=4
②∵ ,
,
∴抛物线顶点D的坐标是(-1,5),AB的中点E的坐标是(-1,4),OA的中点F的坐标是(-1,2),
∴m的取值范围为l<m<3.

17. (2011浙江省,24,14分)如图,在直角坐标系中,抛物线 (a≠0)与x轴交与点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.
(a≠0)与x轴交与点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.
(1)求此抛物线的解析式及顶点D的坐标;
(2)问点P在何处时,线段PQ最长,最长为多少?
(3)设E为线段OC上的三等分点,链接EP,EQ,若EP=EQ,求点P的坐标.


[答案]:(1)由题意,得:
 解得:
解得:
∴ =
= ,顶点坐标为(1,4).
,顶点坐标为(1,4).
(2)由题意,得 P(x, x-1) ,Q (x,  ),
),
∴ 线段PQ= -( x-1)=
-( x-1)=  =
= 
当x= 时,线段PQ最长为
时,线段PQ最长为 。
。
(3)∵E为线段OC上的三等分点,OC=3, ∴E(0,1),或E(0,2)
∵EP=EQ,PQ与y轴平行,
∴ 2×OE= +( x-1)
+( x-1)
当OE=1时,x1=0,x2=3,点P坐标为(0,-1)或(3,2)。
当OE=2时,x1=1,x2=2, 点P坐标为(1,0)或(2,1)。
16. (2011山东日照,24,10分)如图,抛物线y=ax2+bx(a 0)与双曲线y=
0)与双曲线y= 相交于点A,B. 已知点B的坐标为(-2,-2),点A在第一象限内,且tan∠AOx=4. 过点A作直线AC∥x轴,交抛物线于另一点C.
相交于点A,B. 已知点B的坐标为(-2,-2),点A在第一象限内,且tan∠AOx=4. 过点A作直线AC∥x轴,交抛物线于另一点C.
(1)求双曲线和抛物线的解析式;
(2)计算△ABC的面积;
(3)在抛物线上是否存在点D,使△ABD的面积等于△ABC的面积.若存在,请你写出点D的坐标;若不存在,请你说明理由.

[答案](1)把点B(-2,-2)的坐标,代入y= ,
,
得:-2= ,∴k=4.
,∴k=4.
即双曲线的解析式为:y= .
.
设A点的坐标为(m,n)。∵A点在双曲线上,∴mn=4.…①
又∵tan∠AOx=4,∴ =4, 即m=4n.…②
=4, 即m=4n.…②
又①,②,得:n2=1,∴n=±1.
∵A点在第一象限,∴n=1,m=4 , ∴A点的坐标为(1,4)
把A、B点的坐标代入y=ax2+b x,得: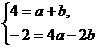 解得a=1,b=3;
解得a=1,b=3;
∴抛物线的解析式为:y=x2+3x ;(2)∵AC∥x轴,∴点C的纵坐标y=4,
代入y=x2+3x,得方程x2+3x-4=0,解得x1=-4,x2=1(舍去).
∴C点的坐标为(-4,4),且AC=5,
又△ABC的高为6,∴△ABC的面积= ×5×6=15 ;
×5×6=15 ;
(3)存在D点使△ABD的面积等于△ABC的面积.
过点C作CD∥AB交抛物线于另一点D .
因为直线AB相应的一次函数是:y=2x+2,且C点的坐标为(-4,4),CD∥AB,
所以直线CD相应的一次函数是:y=2x+12.
解方程组 得
得 所以点D的坐标是(3,18)
所以点D的坐标是(3,18)
15. (2011广东广州市,24,14分)
已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,点A的坐标是(1,0).
(1)求c的值;
(2)求a的取值范围;
(3)该二次函数的图象与直线y=1交于C、D两点,设A、B、C、D四点构成的四边形的对角线相交于点P,记△PCD的面积为S1,△PAB的面积为S2,当0<a<1时,求证:S1-S2为常数,并求出该常数.
[答案](1)c=1
(2)将C(0,1),A(1,0)得
a+b+1=0
故b=―a―1
由b2-4ac>0,可得
(-a-1)2-4a>0
即(a-1)2>0
故a≠1,又a>0
所以a的取值范围是a>0且a≠1.
(3)由题意0<a<1,b=―a―1可得->1,故B在A的右边,B点坐标为(--1,0)
C(0,1),D(-,1)
|AB|=--1-1=--2
|CD|=-
S1-S2=S△CDA-SABC=×|CD|×1-×|AB|×1
=×(-)×1-×(--2)×1
=1
所以S1-S2为常数,该常数为1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com