
题目列表(包括答案和解析)
6. (2011山东济宁,22,8分)数学课上,李老师出示了这样一道题目:如图 ,正方形
,正方形 的边长为
的边长为 ,
,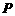 为边
为边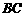 延长线上的一点,
延长线上的一点,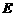 为
为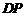 的中点,
的中点,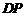 的垂直平分线交边
的垂直平分线交边 于
于 ,交边
,交边 的延长线于
的延长线于 .当
.当 时,
时, 与
与 的比值是多少?
的比值是多少?
经过思考,小明展示了一种正确的解题思路:过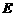 作直线平行于
作直线平行于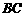 交
交 ,
, 分别于
分别于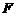 ,
, ,如图
,如图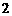 ,则可得:
,则可得: ,因为
,因为 ,所以
,所以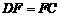 .可求出
.可求出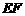 和
和 的值,进而可求得
的值,进而可求得 与
与 的比值.
的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究,得出了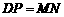 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.


(1)解:过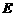 作直线平行于
作直线平行于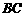 交
交 ,
, 分别于点
分别于点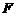 ,
, ,
,
则 ,
, ,
,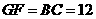 .
.
∵ ,∴
,∴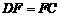 .····························································································· 2分
.····························································································· 2分
∴ ,
, .
.
∴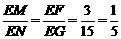 . ···································································································· 4分
. ···································································································· 4分
(2)证明:作 ∥
∥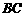 交
交 于点
于点 ,················································································ 5分
,················································································ 5分
则 ,
, .
.
∵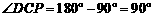 ,
,
∴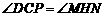 .
.
∵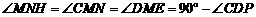 ,
,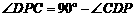 ,
,
∴ .∴
.∴ .······························································ 7分
.······························································ 7分
∴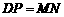 .····················································································································· 8分
.····················································································································· 8分
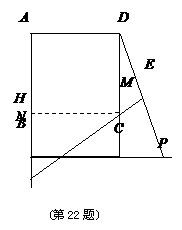

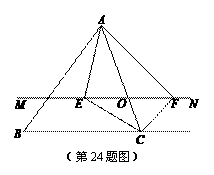
5. (2011山东滨州,24,10分)如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF。那么当点O运动到何下时,四边形AECF是矩形?并证明你的结论。

[答案]

当点O运动到AC的中点(或OA=OC)时,
四边形AECF是矩形………………2分
证明:∵CE平分∠BCA,∴∠1=∠2,………………3分
又∵MN∥BC, ∴∠1=∠3,
∴∠3=∠2,∴EO=CO. ………………5分
同理,FO=CO………………6分
∴EO=FO
又OA=OC, ∴四边形AECF是平行四边形………………7分
又∵∠1=∠2,∠4=∠5,
∴∠1+∠5=∠2+∠4. ………………8分
又∵∠1+∠5+∠2+∠4=180°
∴∠2+∠4=90°………………9分
∴四边形AECF是矩形………………10分
4. (2011广东广州市,18,9分)
如图4,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.
求证:△ACE≌△ACF.
|


[答案]∵四边形ABCD为菱形
∴∠BAC=∠DAC
又∵AE=AF,AC=AC
∴△ACE≌△ACF(SAS)
3. (2011福建福州,21,12分)已知,矩形 中,
中, ,
,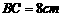 ,
, 的垂直平分线
的垂直平分线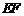 分别交
分别交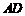 、
、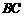 于点
于点 、
、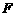 ,垂足为
,垂足为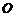 .
.
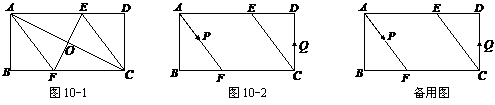
(1)如图10-1,连接 、
、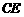 .求证四边形
.求证四边形 为菱形,并求
为菱形,并求 的长;
的长;
(2)如图10-2,动点 、
、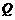 分别从
分别从 、
、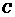 两点同时出发,沿
两点同时出发,沿 和
和 各边匀速运动一周.即点
各边匀速运动一周.即点 自
自 →
→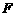 →
→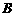 →
→ 停止,点
停止,点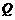 自
自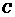 →
→ →
→ →
→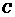 停止.在运动过程中,
停止.在运动过程中,
①已知点 的速度为每秒5
的速度为每秒5 ,点
,点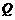 的速度为每秒4
的速度为每秒4 ,运动时间为
,运动时间为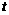 秒,当
秒,当 、
、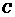 、
、 、
、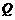 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求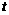 的值.
的值.
②若点 、
、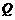 的运动路程分别为
的运动路程分别为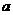 、
、 (单位:
(单位: ,
,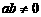 ),已知
),已知 、
、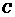 、
、 、
、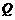 四点为顶点的四边形是平行四边形,求
四点为顶点的四边形是平行四边形,求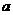 与
与 满足的数量关系式.
满足的数量关系式.

[答案](1)证明:①∵四边形 是矩形
是矩形
∴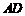 ∥
∥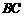
∴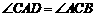 ,
,
∵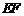 垂直平分
垂直平分 ,垂足为
,垂足为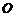
∴
∴ ≌
≌
∴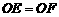
∴四边形 为平行四边形
为平行四边形
又∵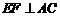
∴四边形 为菱形
为菱形
②设菱形的边长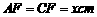 ,则
,则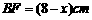
在 中,
中,
由勾股定理得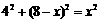 ,解得
,解得
∴
(2)①显然当 点在
点在 上时,
上时,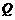 点在
点在 上,此时
上,此时 、
、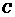 、
、 、
、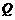 四点不可能构成平行四边形;同理
四点不可能构成平行四边形;同理 点在
点在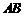 上时,
上时,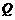 点在
点在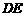 或
或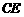 上,也不能构成平行四边形.因此只有当
上,也不能构成平行四边形.因此只有当 点在
点在 上、
上、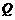 点在
点在 上时,才能构成平行四边形
上时,才能构成平行四边形
∴以 、
、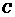 、
、 、
、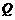 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,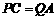
∵点 的速度为每秒5
的速度为每秒5 ,点
,点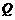 的速度为每秒4
的速度为每秒4 ,运动时间为
,运动时间为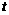 秒
秒
∴ ,
,
∴ ,解得
,解得
∴以 、
、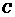 、
、 、
、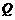 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时, 秒.
秒.
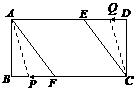

②由题意得,以 、
、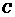 、
、 、
、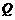 四点为顶点的四边形是平行四边形时,点
四点为顶点的四边形是平行四边形时,点 、
、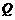 在互相平行的对应边上.
在互相平行的对应边上.
分三种情况:
i)如图1,当 点在
点在 上、
上、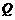 点在
点在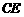 上时,
上时,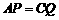 ,即
,即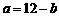 ,得
,得
ii)如图2,当 点在
点在 上、
上、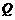 点在
点在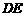 上时,
上时, , 即
, 即 ,得
,得
iii)如图3,当 点在
点在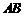 上、
上、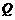 点在
点在 上时,
上时,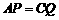 ,即
,即 ,得
,得
综上所述, 与
与 满足的数量关系式是
满足的数量关系式是
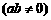


2. (2011安徽,23,14分)如图,正方形ABCD的四个顶点分别在四条平行线 、
、 、
、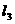 、
、 上,这四条直线中相邻两条之间的距离依次为
上,这四条直线中相邻两条之间的距离依次为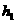 、
、 、
、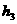 (
(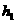 >0,
>0, >0,
>0,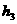 >0).
>0).
(1)求证: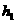 =
=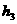 ;
;


(2)设正方形ABCD的面积为S,求证:S= ;
;
(3)若 ,当
,当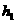 变化时,说明正方形ABCD的面积S随
变化时,说明正方形ABCD的面积S随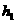 的变化情况.
的变化情况.


[答案](1)过A点作AF⊥l3分别交l2、l3于点E、F,过C点作CG⊥l3交l3于点G,
∵l2∥l3,∴∠2 =∠3,∵∠1+∠2=90°,∠4+∠3=90°,∴∠1=∠4,又∵∠BEA=∠DGC=90°, BA=DC,∴△BEA≌△DGC,∴AE=CG,即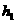 =
=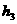 ;
;
(2)∵∠FAD+∠3=90°,∠4+∠3=90°,∴∠FAD =∠4,又∵∠AFD=∠DGC=90°, AD=DC,∴△AFD≌△DGC,∴DF=CG,∵AD2=AF2+FD2,∴S= ;
;
(3)由题意,得 , 所以
, 所以
 ,
,
又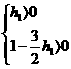 ,解得0<h1<
,解得0<h1<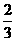
∴当0<h1<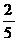 时,S随h1的增大而减小;
时,S随h1的增大而减小;
当h1=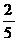 时,S取得最小值
时,S取得最小值 ;
;
当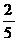 <h1<
<h1<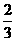 时,S随h1的增大而增大.
时,S随h1的增大而增大.
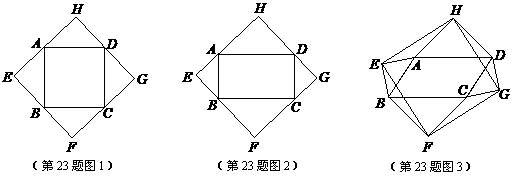
1. (2011浙江省舟山,23,10分)以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形EFGH.
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC= (0°<
(0°< <90°),
<90°),
① 试用含 的代数式表示∠HAE;
的代数式表示∠HAE;
② 求证:HE=HG;
③ 四边形EFGH是什么四边形?并说明理由.

[答案](1)四边形EFGH是正方形.
(2) ①∠HAE=90°+a.
在□ABCD中,AB∥CD,∴∠BAD=180°-∠ADC=180°-a;
∵△HAD和△EAB都是等腰直角三角形,∴∠HAD=∠EAB=45°,
∴∠HAE=360°-∠HAD-∠EAB-∠BAD=360°-45°-45°-(180°-a)=90°+a.
②∵△AEB和△DGC都是等腰直角三角形,∴AE= AB,DG=
AB,DG= CD,
CD,
在□ABCD中,AB=CD,∴AE=DG,∵△HAD和△GDC都是等腰直角三角形,
∴∠DHA=∠CDG= 45°,∴∠HDG=∠HAD+∠ADC+∠CDG=90°+a=∠HAE.
∵△HAD是等腰直角三角形,∴HA=HD,∴△HAE≌△HDG,∴HE=HG.
③四边形EFGH是正方形.
由②同理可得:GH=GF,FG=FE,∵HE=HG(已证),∴GH=GF=FG=FE,∴四边形EFGH是菱形;∵△HAE≌△HDG(已证),∴∠DHG=∠AHE,又∵∠AHD=∠AHG+∠DHG=90°,∴∠EHG=∠AHG+∠AHE=90°,∴四边形EFGH是正方形.
24.
23.
22. (2010湖北孝感,16,3分)已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是 .
[答案]15°或75°
21. (2011河北,14,3分)如图6,已知菱形ABCD,其顶点A,B在数轴对应的数分别为-4和1,则BC=__.
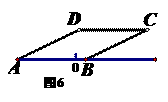
[答案]5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com