
题目列表(包括答案和解析)
14. (2011湖北襄阳,21,6分)
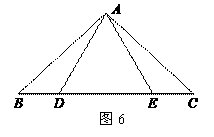
如图6,点D,E在△ABC的边BC上,连接AD,AE. ①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①② ③;①③
③;①③ ②;②③
②;②③ ①.
①.
(1)以上三个命题是真命题的为(直接作答) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).

[答案](1)①② ③;①③
③;①③ ②;②③
②;②③ ①.················································· 3分
①.················································· 3分
(2)(略) 6分
13. (2011湖北黄冈,18,7分)如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若AE=4,FC=3,求EF长.


[答案]连结BD,证△BED≌△CFD和△AED≌△BFD,求得EF=5
12. (2011广东省,21,9分)如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止.不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2).
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据2的情况说明理由);
(3)问:当x为何值时,△AGH是等腰三角形?

[解](1)△HGA及△HAB;
(2)由(1)可知△AGC∽△HAB
∴ ,即
,即 ,
,
所以,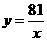
(3)当CG< 时,∠GAC=∠H<∠HAC,∴AC<CH
时,∠GAC=∠H<∠HAC,∴AC<CH
∵AG<AC,∴AG<GH
又AH>AG,AH>GH
此时,△AGH不可能是等腰三角形;
当CG= 时,G为BC的中点,H与C重合,△AGH是等腰三角形;
时,G为BC的中点,H与C重合,△AGH是等腰三角形;
此时,GC=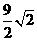 ,即x=
,即x=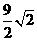
当CG> 时,由(1)可知△AGC∽△HGA
时,由(1)可知△AGC∽△HGA
所以,若△AGH必是等腰三角形,只可能存在AG=AH
若AG=AH,则AC=CG,此时x=9
综上,当x=9或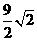 时,△AGH是等腰三角形.
时,△AGH是等腰三角形.
11. (2011江苏扬州,23,10分)已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。

[答案](1)证明:∵OB=OC ∴∠OBC=∠OCB
∵BD、CE是两条高 ∴∠BDC=∠CEB=90°
又∵BC=CB ∴△BDC≌△CEB(AAS)
∴∠DBC=∠ECB ∴AB=AC
∴△ABC是等腰三角形。
(2)点O是在∠BAC的角平分线上。连结AO.

∵ △BDC≌△CEB ∴DC=EB,
∵OB=OC ∴ OD=OE
又∵∠BDC=∠CEB=90° AO=AO
∴△ADO≌△AEO(HL)
∴∠DAO=∠EAO
∴点O是在∠BAC的角平分线上。
10.(2011重庆綦江,24,10分)如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连结BE.
(1) 求证:△ACD≌△BCE;
(2) 延长BE至Q, P为BQ上一点,连结CP、CQ使CP=CQ=5, 若BC=8时,求PQ的长.

[答案]:(1)证明ABC和△CDE均为等边三角形,
∴AC=BC , CD=CE
且∠ACB=∠DCE=60°
∵∠ACD+∠DCB=∠DCB+∠BCE=60°
∴∠ACD=∠BCE
∴△ACD≌△BCE

(2)解:作CH⊥BQ交BQ于H, 则PQ=2HQ
在Rt△BHC中 ,由已知和(1)得∠CBH=∠CAO=30°,∴ CH=4
在Rt△CHQ中,HQ=
∴PQ=2HQ=6
9. (2011广东株洲,20,6分)如图, △ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.

[答案](1)解法一:∵DE垂直平分AC,∴CE=AE,∠ECD=∠A=36°.
解法二:∵DE垂直平分AC,∴AD=CD,∠ADE=∠CDE=90°,
又∵DE =DE,∴△ADE≌△CDE,∠ECD=∠A=36°.
(2)解法一:∵AB=AC,∠A=36°,∴∠B=∠ACB=72°,
∵∠ECD=36°,
∴∠BCE=∠ACB-∠ECD=36°,
∠BEC=72°=∠B,
∴ BC=EC=5.
解法二:∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∴∠BEC=∠A+∠ECD=72°,
∴∠BEC=∠B,
∴BC=EC=5.
8. (2011浙江义乌,23,10分)如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点P与点C不重合),连结BP. 将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连结AA1,射线AA1分别交射线PB、射线B1B于点E、F.
(1) 如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP始终存在 ▲ 关系(填“相似”或“全等”),并说明理由;
(2)如图2,设∠ABP=β . 当60°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图3,当α=60°时,点E、F与点B重合. 已知AB=4,设DP=x,△A1BB1的面
积为S,求S关于x的函数关系


[答案](1) 相似
由题意得:∠APA1=∠BPB1=α AP= A1P BP=B1P
则 ∠PAA1 =∠PBB1 =
∵∠PBB1 =∠EBF ∴∠PAE=∠EBF
又∵∠BEF=∠AEP
∴△BEF ∽△AEP
(2)存在,理由如下:
易得:△BEF ∽△AEP
若要使得△BEF≌△AEP,只需要满足BE=AE即可
∴∠BAE=∠ABE
∵∠BAC=60° ∴∠BAE=
∵∠ABE=β ∠BAE=∠ABE
∴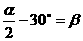 即α=2β+60°
即α=2β+60°
(3)连结BD,交A1B1于点G,
过点A1作A1H⊥AC于点H.


∵∠B1 A1P=∠A1PA=60° ∴A1B1∥AC
由题意得:AP= A1 P ∠A=60°
∴△PAA1是等边三角形
∴A1H= 在Rt△ABD中,BD=
在Rt△ABD中,BD=
∴BG=
∴ (0≤x<2)
(0≤x<2)
7. (2011浙江台州,23,12分)如图1,过△ABC的顶点A分别做对边BC上的高AD和中线AE,点D是垂足,点E是BC中点,规定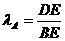 。特别的,当点D重合时,规定
。特别的,当点D重合时,规定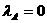 。另外。对
。另外。对 、
、 作类似的规定。
作类似的规定。
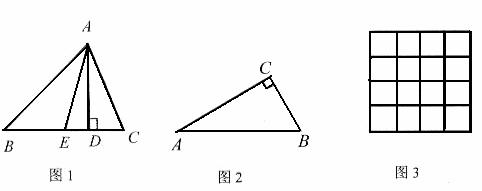
(1)如图2,已知在Rt△ABC中,∠A=30º,求 、
、 ;
;
(2)在每个小正方形边长为1的4×4方格纸上,画一个△ABC,使其顶点在格点(格点即每个小正方形的顶点)上,且 ,面积也为2;
,面积也为2;
(3)判断下列三个命题的真假。(真命题打√,假命题打×)
① 若△ABC中, ,则△ABC为锐角三角形;( )
,则△ABC为锐角三角形;( )
② 若△ABC中, ,则△ABC为直角三角形;( )
,则△ABC为直角三角形;( )
③ 若△ABC中,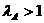 ,则△ABC为钝角三角形;( )
,则△ABC为钝角三角形;( )
[答案]解:(1)如图,作CD⊥AB,垂足为D,作中线CE、AF。
∴ =1
=1
∵ Rt△ABC中,∠CAB=30º, ∴ AE=CE=BE ,∠CEB=60º,
∴△CEB是正三角形,
∵ CD⊥AB ∴ AE=2DE
∴ =
= ; ∴
; ∴ =1,
=1, =
= ;
;
(2)如图所示:

(3)①×;②√;③√。
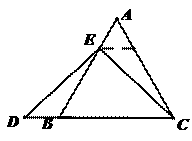
6. (2011浙江绍兴,23,12分)数学课上,李老师出示了如下框中的题目.
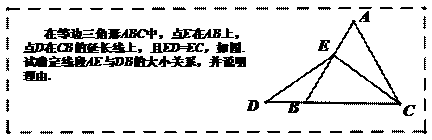
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点 为
为 的中点时,如图1,确定线段
的中点时,如图1,确定线段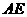 与
与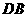 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:
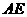
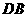 (填“>”,“<”或“=”).
(填“>”,“<”或“=”).
|
|

(2)特例启发,解答题目
解:题目中,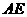 与
与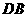 的大小关系是:
的大小关系是: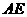
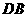 (填“>”,“<”或“=”).理由如下:如图2,过点
(填“>”,“<”或“=”).理由如下:如图2,过点 作
作 ,交
,交 于点
于点 .
.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形 中,点
中,点 在直线
在直线 上,点
上,点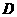 在直线
在直线 上,且
上,且 .若
.若 的边长为1,
的边长为1,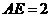 ,求
,求 的长(请你直接写出结果).
的长(请你直接写出结果).
[答案](1)= .
(2)=.
方法一:如图,等边三角形 中,
中,



 是等边三角形,
是等边三角形,


又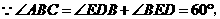

.
方法二:在等边三角形 中,
中,

而由 是正三角形可得
是正三角形可得

(3)1或3.
5. (2011浙江衢州,23,10分) 是一张等腰直角三角形纸板,
是一张等腰直角三角形纸板, .
.
要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲、乙两种剪法,哪种剪法所得的正方形面积更大?请说明理由.


图1中甲种剪法称为第1次剪取,记所得的正方形面积为 ;按照甲种剪法,在余下的
;按照甲种剪法,在余下的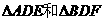 中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为
中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为 (如图2),则
(如图2),则 ;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形的面积和为
;再在余下的四个三角形中,用同样的方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形的面积和为 (如图3);继续操作下去…则第10次剪取时,
(如图3);继续操作下去…则第10次剪取时, .
.
求第10次剪取后,余下的所有小三角形的面积和.
[答案](1)解法1:如图甲,由题意得 .如图乙,设
.如图乙,设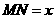 ,则由题意,得
,则由题意,得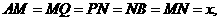

又
 甲种剪法所得的正方形的面积更大
甲种剪法所得的正方形的面积更大
说明:图甲可另解为:由题意得点D、E、F分别为 的中点,
的中点,
解法2:如图甲,由题意得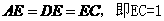
如图乙,设

 甲种剪法所得的正方形的面积更大
甲种剪法所得的正方形的面积更大
(2)
(3)
(3)解法1:探索规律可知: ‘
‘
剩余三角形的面积和为:
解法2:由题意可知,
第一次剪取后剩余三角形面积和为
第二次剪取后剩余三角形面积和为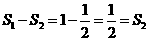
第三次剪取后剩余三角形面积和为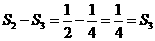
…
第十次剪取后剩余三角形面积和为

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com