
题目列表(包括答案和解析)
15、(2011•菏泽)(1)计算: ﹣(4﹣π)0﹣6cos30°+|﹣2|;
﹣(4﹣π)0﹣6cos30°+|﹣2|;
(2)已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:AB=DC.

考点:特殊角的三角函数值;零指数幂;全等三角形的判定与性质。
专题:计算题;证明题。
分析:(1)本题涉及零指数幂、特殊角的三角函数值、二次根式化简,针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
(2)根据全等三角形的判定定理,结合题意即可运用SAS进行全等的判断,然后即可得出结论.
解答:解:(1)解:原式= =1;
=1;
(2)证明:在△ABC与△DCB中
AC平分∠BCD,BD平分∠ABC,
∴△ABC≌△DCB.
∴AB=DC.
点评:本题考查特殊角的三角函数值及全等三角形的判断,属于基础题的综合运用,比较简单,关键还是基本知识的掌握.
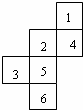
14、(2011•菏泽)填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值是 158 .

考点:规律型:数字的变化类。
专题:规律型。
分析:分析前三个正方形可知,规律为右上和左下两个数的积减左上的数等于右下的数,且左上,左下,右上三个数是相邻的偶数.因此,图中阴影部分的两个数分别是左下是12,右上是14.
解答:解:分析可得图中阴影部分的两个数分别是左下是12,右上是14,
则m=12×14﹣10=158.
故答案为:158.
点评:本题是一道找规律的题目,要求学生的通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题.解决本题的难点在于找出阴影部分的数.
13、从﹣2,﹣1,0,1,2这五个数中任取一个数,作为关于x的一元二次方程x2﹣x+k=0中的k值,则所得的方程中有两个不相等的实数根的概率是 .
.
考点:概率公式;根的判别式。
分析:所得的方程中有两个不相等的实数根,根的判别式△=b2﹣4ac的值大于0,将各个值代入,求出值后,再计算出概率即可.
解答:解:△=b2﹣4ac=1﹣4k,将﹣2,﹣1,0,1,2分别代入得9,5,1,﹣3,﹣7,大于0的情况有三种,故概率为 .
.
点评:总结:一元二次方程根的情况与判别式△的关系:
(1)△>0⇔方程有两个不相等的实数根;
(2)△=0⇔方程有两个相等的实数根;
(3)△<0⇔方程没有实数根.
用到的知识点为:概率=所求情况数与总情况数之比.
12、(2011•菏泽)如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值的是 6 .
考点:专题:正方体相对两个面上的文字。
专题:计算题;几何图形问题。
分析:根据相对的面相隔一个面得到相对的2个数,相加后比较即可.
解答:解:易得2和6是相对的两个面;3和4是相对两个面;1和5是相对的2个面,
∵2+6=8,3+4=7,1+5=6,
所以原正方体相对两个面上的数字和最小的是6,.
故答案为:6..
点评:本题考查了正方体相对两个面上的文字,解决本题的关键是根据相对的面的特点得到相对的两个面上的数字.
11、(2011•菏泽)在一次信息技术考试中,某兴趣小组8名同学的成绩(单位:分)分别是:7,10,9,8,7,9,9,8,则这组数据的中位数是 8.5 .
考点:中位数。
专题:应用题。
分析:找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数.
解答:解:题目中数据共有8个,按从小到大排列后为:7、7、8、8、9、9、9、10.
故中位数是按从小到大排列后第4,第5两个数的平均数作为中位数,
故这组数据的中位数是 ×(8+9)=8.5.
×(8+9)=8.5.
故答案为:8.5.
点评:本题属于基础题,考查了确定一组数据的中位数的能力.注意:找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.
10、(2010•宜宾)分解因式:2a2﹣4a+2= 2(a﹣1)2.
考点:提公因式法与公式法的综合运用。
专题:计算题。
分析:先提公因式2,再利用完全平方公式分解因式即可.
解答:解:2a2﹣4a+2,
=2(a2﹣2a+1),
=2(a﹣1)2.
点评:本题考查用提公因式法和公式法进行因式分解的能力,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
9、(2011•菏泽)使 有意义的x的取值范围是 x≥
有意义的x的取值范围是 x≥ .
.
考点:二次根式有意义的条件。
专题:计算题。
分析:本题主要考查自变量的取值范围,函数关系中主要有二次根式.根据二次根式的意义,被开方数是非负数.
解答:解:根据题意得:4x﹣1≥0,
解得x≥ .
.
故答案为x≥ .
.
点评:函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.
8、(2011•菏泽)如图为抛物线y=ax2+bx+c的图象,A、B、C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
A、a+b=﹣1 B、a﹣b=﹣1
C、b<2a D、ac<0
考点:抛物线与x轴的交点;二次函数图象上点的坐标特征。
专题:计算题。
分析:根据OA=OC=1和图象得到C(0,1),A(﹣1,0),把C(0,1)代入求出c=1,把A(﹣1,0)代入即可求出答案.
解答:解:∵OA=OC=1,
∴由图象知:C(0,1),A(﹣1,0),
把C(0,1)代入得:c=1,
把A(﹣1,0)代入得:a﹣b=﹣1,
故选B.
点评:本题主要考查对抛物线与X轴的交点,二次函数图象上点的坐标特征等知识点的理解和掌握,能求出A、C的坐标是解此题的关键.
7、某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打( )
A、6折 B、7折
C、8折 D、9折
考点:一元一次不等式的应用。
分析:本题可设打x折,根据保持利润率不低于5%,可列出不等式:1200x×0.1≥800(1+0.05),解出x的值即可得出打的折数.
解答:解:设可打x折,则有1200x×0.1≥800(1+0.05)
120x≥840
x≥7
故选B
点评:本题考查的是一元一次不等式的应用,解此类题目时注意利润和折数,计算折数时要注意要乘以0.1.
6、(2011•菏泽)定义一种运算☆,其规则为a☆b=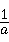 +
+ ,根据这个规则,计算2☆3的值是( )
,根据这个规则,计算2☆3的值是( )
A、 B、
B、
C、5 D、6
考点:代数式求值。
专题:新定义。
分析:由a☆b=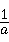 +
+ ,可得2☆3=
,可得2☆3= +
+ ,则可求得答案.
,则可求得答案.
解答:解:∵a☆b=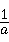 +
+ ,
,
∴2☆3= +
+ =
= .
.
故选A.
点评:此题考查了新定义题型.解题的关键是理解题意,根据题意解题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com