
题目列表(包括答案和解析)
10、(2011•临沂)如图,A、B是数轴上两点.在线段AB上任取一点C,则点C到表示﹣1的点的距离不大于2的概率是( )
A、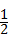 B、
B、
C、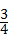 D、
D、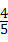
考点:概率公式;数轴。
专题:计算题。
分析:将数轴上A到表示﹣1的点之间的距离不大于2、表1的点到表示﹣1 的点间的距离不大于2,而AB间的距离分为5段,利用概率公式即可解答.
解答:解:如图,C1与C2到表示﹣1的点的距离均不大于2,根据概率公式P=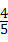 .
.
故选D.

点评:此题结合几何概率考查了概率公式,将AB间的距离分段,利用符合题意的长度比上AB的长度即可.
9、(2011•临沂)如图是一圆锥的主视图,则此圆锥的侧面展开图的圆心角的度数是( )
A、60° B、90°
C、120° D、180°
考点:圆锥的计算。
专题:计算题。
分析:根据圆锥的主视图可以得到圆锥的母线长和圆锥的底面直径,求出圆锥的底面周长就是侧面展开扇形的弧长,代入公式求得即可.
解答:解:圆锥的主视图可以得到圆锥的母线长12cm和圆锥的底面直径6cm,
∴圆锥的底面周长为:πd=6πcm,
∵圆锥的侧面展开扇形的弧长等于圆锥的侧面展开扇形的弧长,
∴圆锥的侧面展开扇形的弧长为6πcm,
∴圆锥的侧面展开扇形的面积为: =
=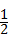 ×6π×12=36π,
×6π×12=36π,
∴ =36,
=36,
解得:n=90.
故选B.
点评:本题考查了圆锥的计算,解题的关键是正确的理解圆锥和侧面扇形的关系.
8、(2011•临沂)不等式组 的解集是( )
的解集是( )
A、x≥8 B、3<x≤8
C、0<x<2 D、无解
考点:解一元一次不等式组。
专题:计算题。
分析:分别求出各不等式的解集,再求出其公共解集即可.
解答:解: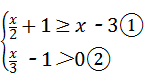 ,
,
由①得,x≤8,
由②得,x>3,
故此不等式组的解集为:3<x≤8.
故答案为:3<x≤8.
点评:本题考查的是解一元一此不等式组,解答此题的关键是熟知解一元一此不等式组应遵循的法则,同大取较大,同小取较小,小大大小中间找,大大小小解不了.
7、(2011•临沂)在一次九年级学生视力检查中.随机检查了8个人的右眼视力,结果如下:4.0,4.2,4.5,4.0,4.4,4.5,4.0,4.8.则下列说法中正确的是( )
A、这组数据的中位数是4.4 B、这组数据的众数是4.5
C、这组数据的平均数是4.3 D、这组数据的极差是0.5
考点:极差;算术平均数;中位数;众数。
专题:计算题。
分析:分别计算这组数据的中位数,众数、平均数及方差后找到正确的选项即可.
解答:解:将这组数据排序后为:4.0、4.0、4.0、4.2、4.4、4.5、4.5、4.8,
∴中位数为: =4.3,
=4.3,
∴A选项错误;
∵4.0出现了3次,最多,
∴众数为4.0,
∴B选项错误;
∵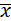 =
= (4.0+4.0+4.0+4.2+4.4+4.5+4.5+4.8)=4.3,
(4.0+4.0+4.0+4.2+4.4+4.5+4.5+4.8)=4.3,
∴C选项正确.
故选C.
点评:本题考查了平均数、中位数、众数及极差的知识,此类考题是中考的必考点,题目相对比较简单.
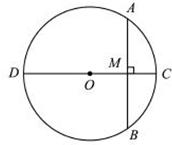
6、(2011•临沂)如图,⊙O的直径CD=5cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5.则AB的长是( )
A、2cm B、3cm
C、4cm D、2 cm
cm
考点:垂径定理;勾股定理。
专题:探究型。
分析:先连接OA,由CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为M可知AB=2AM,再根据CD=5cm,OM:OD=3:5可求出OM的长,在Rt△AOM中,利用勾股定理即可求出AM的长,进而可求出AB的长.
解答:解:连接OA,
∵CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,
∴AB=2AM,
∵CD=5cm,
∴OD=OA=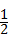 CD=
CD=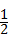 ×5=
×5=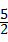 cm,
cm,
∵OM:OD=3:5,
∴OM= OD=
OD= ×
×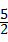 =
= ,
,
∴在Rt△AOM中,AM= =
=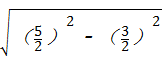 =2,
=2,
∴AB=2AM=2×2=4cm.
故选C.

点评:本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
5、(2011•临沂)化简(x﹣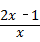 )÷(1﹣
)÷(1﹣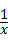 )的结果是( )
)的结果是( )
A、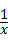 B、x﹣1
B、x﹣1
C、 D、
D、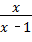
考点:分式的混合运算。
分析:首先利用分式的加法法则,求得括号里面的值,再利用除法法则求解即可求得答案.
解答:解:(x﹣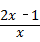 )÷(1﹣
)÷(1﹣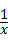 ),
),
=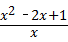 ÷
÷ ,
,
= •
•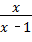 ,
,
=x﹣1.
故选B.
点评:此题考查了分式的混合运算.解题时要注意运算顺序.
4、(2011•临沂)计算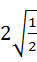 ﹣6
﹣6 +
+ 的结果是( )
的结果是( )
A、3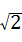 ﹣2
﹣2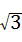 B、5﹣
B、5﹣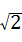
C、5﹣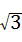 D、2
D、2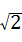
考点:二次根式的加减法。
分析:根据二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并.
解答:解: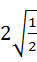 ﹣6
﹣6 +
+
=2× ﹣6×
﹣6×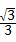 +2
+2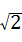 ,
,
=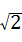 ﹣2
﹣2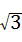 +2
+2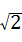 ,
,
=3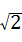 ﹣2
﹣2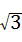 .
.
故选A.
点评:此题主要考查了二次根式的运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并.合并同类二次根式的实质是合并同类二次根式的系数,根指数与被开方数不变.
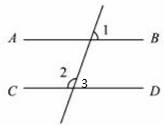
3、(2011•临沂)如图.己知AB∥CD,∠1=70°,则∠2的度数是( )
A、60° B、70°
C、80° D、110
考点:平行线的性质。
分析:由AB∥CD,根据两直线平行,同位角相等,即可求得∠2的度数,又由邻补角的性质,即可求得∠2的度数.
解答:解:∵AB∥CD,
∴∠1=∠3=70°,
∵∠2+∠3=180°,
∴∠2=110°.
故选D.
点评:此题考查了平行线的性质.注意数形结合思想的应用.
2、(2011•临沂)下列运算中正确的是( )
A、(﹣ab)2=2a2b2 B、(a+b)2=a2+1
C、a6÷a2=a3 D、2a3+a3=3a3
考点:同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方。
分析:积的乘方等于把积的每一个因式分别乘方,再把所得的幂相乘;完全平方公式:两数和的平方等于它们的平方和加上它们积的2倍;同底数幂的除法,底数不变指数相减;合并同类项,系数相加字母和字母的指数不变;根据法则一个个筛选.
解答:解:A、(﹣ab)2=(﹣1)2a2b2=a2b2,故此选项错误;
B、(a+b)2=a2+2ab+b2,故此选项错误;
C、a6÷a2=a6﹣2=a4,故此选项错误;
D、2a3+a3=(2+1)a3=3a3,故此选项正确.
故选D.
点评:此题主要考查了积的乘方,完全平方公式,同底数幂的除法,合并同类项的计算,一定要记准法则才能做题.
1、(2011•临沂)下列各数中,比﹣1小的数是( )
A、0 B、1
C、﹣2 D、2
考点:有理数大小比较。
专题:探究型。
分析:根据有理数比较大小的法则进行比较即可.
解答:解:∵﹣1是负数,
∴﹣1<0,故A错误;
∵2>1>0,
∴2>1>0>﹣1,故B、D错误;
∵|﹣2|>|﹣1|,
∴﹣2<﹣1,故C正确.
故选C.
点评:本题考查的是有理数大小比较的法则:
①正数都大于0;
②负数都小于0;
③正数大于一切负数;
④两个负数,绝对值大的其值反而小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com