
题目列表(包括答案和解析)
7. (2011山东聊城,18,7分)解方程: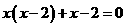
[答案](x-2)(x+1)=0,解得x=2或x=-1
6. (2011江苏苏州,22,6分)已知|a-1|+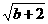 =0,求方程
=0,求方程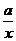 +bx=1的解.
+bx=1的解.
[答案]解:由|a-1|+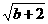 =0,得a=1,b=-2.
=0,得a=1,b=-2.
由方程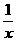 -2x=1得2x2+x-1=0
-2x=1得2x2+x-1=0
解之,得x1=-1,x2=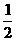 .
.
经检验,x1=-1,x2=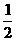 是原方程的解.
是原方程的解.
5. (2011浙江义乌,19,6分)商场某种商品平均每天可销售30件,每件盈利50元. 为了尽快减少库存,商场决定采取适当的降价措施. 经调查发现,每件商品每降价1元,商场平均每天可多售出 2件.设每件商品降价x元. 据此规律,请回答:
(1)商场日销售量增加 ▲ 件,每件商品盈利 ▲ 元(用含x的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
[答案](1) 2x 50-x
(2)由题意得:(50-x)(30+2x)=2100
化简得:x2-35x+300=0
解得:x1=15, x2=20
∵该商场为了尽快减少库存,则x=15不合题意,舍去. ∴x=20
答:每件商品降价20元,商场日盈利可达2100元.
4. (2011浙江衢州,21,8分)某花圃用花盆培育某种花苗,经过实验发现每盆的盈利于每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3圆;以同样的栽培条件,若每盆没增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?
小明的解法如下:
解:设每盆花苗增加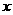 株,则每盆花苗有
株,则每盆花苗有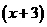 株,平均单株盈利为
株,平均单株盈利为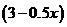 元,由题意,
元,由题意,
得 .
.
化简,整理,的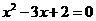 .
.
解这个方程,得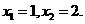
答:要使得每盆的盈利达到10元,每盆应该植入4株或5株.
本题涉及的主要数量有每盆花苗株数,平均单株盈利,每盆花苗的盈利等,请写出两个不同的等量关系:
请用一种与小明不相同的方法求解上述问题。
[答案]解:(1)平均单株盈利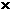 株数=每盆盈利
株数=每盆盈利
平均单株盈利=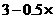 每盆增加的株数
每盆增加的株数
每盆的株数=3+每盆增加的株数
(2)解法1(列表法)
|
平均植入株数 |
平均单株盈利(元) |
每盆盈利(元) |
|
3 |
3 |
9 |
|
4 |
2.5 |
10 |
|
5 |
2 |
10 |
|
6 |
1.5 |
9 |
|
7 |
1 |
7 |
|
… |
… |
… |
答:要使每盆的盈利达到10元,每盆应该植入4株或5株。
解法2(图像法)
如图,纵轴表示平均单株盈利,横坐标表示株数,则相应长方形面积表示每一盆盈利.
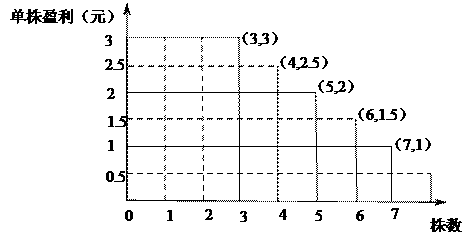
从图像可知,每盆植入4株或5株时,相应长方形面积都是10.
答:要使每盆的盈利达到10元,每盆应该植入4株或5株。
解法3(函数法)
解:设每盆花苗增加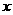 株时,每盆盈利10元,根据题意,得
株时,每盆盈利10元,根据题意,得
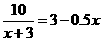
解这个方程,得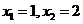
经验证,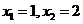 是所列方程的解.
是所列方程的解.
答:要使每盆的盈利达到10元,每盆应该植入4株或5株。
3. (2011四川南充市,18,8分)关于的一元二次方程x2+2x+k+1=0的实数解是x1和x2。
(1)求k的取值范围;
(2)如果x1+x2-x1x2<-1且k为整数,求k的值。
[答案]解:∵(1)方程有实数根 ∴⊿=22-4(k+1)≥0
解得 k≤0
K的取值范围是k≤0
(2)根据一元二次方程根与系数的关系,得x1+x2=-2, x1x2=k+1
x1+x2-x1x2=-2,+ k+1
由已知,得 -2,+ k+1<-1 解得 k>-2
又由(1)k≤0
∴ -2<k≤0
∵ k为整数 ∴k的值为-1和0.
2. (2011山东日照,20,8分)为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2011年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2012年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2012年底共建设了多少万平方米廉租房.
[答案](1)设每年市政府投资的增长率为x,
根据题意,得:2+2(1+x)+2(1+x)2=9.5,
整理,得:x2+3x-1.75=0, 解之,得:x= ,
,
∴x1=0.5 x2=-0.35(舍去),答:每年市政府投资的增长率为50%;
(2)到2012年底共建廉租房面积=9.5÷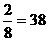 (万平方米).
(万平方米).
1. (2011安徽芜湖,20,8分) 如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(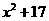 )cm,正六边形的边长为(
)cm,正六边形的边长为(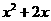 )cm
)cm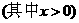 .求这两段铁丝的总长.
.求这两段铁丝的总长. 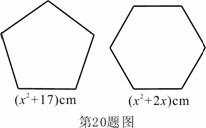
[答案]
解: 由已知得,正五边形周长为5(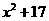 )cm,正六边形周长为6(
)cm,正六边形周长为6(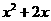 )cm.…2分
)cm.…2分
因为正五边形和正六边形的周长相等,所以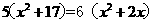 . ………………3分
. ………………3分
整理得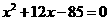 , 配方得
, 配方得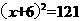 ,解得
,解得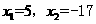 (舍去).………6分
(舍去).………6分
故正五边形的周长为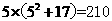 (cm). …………………………………………7分
(cm). …………………………………………7分
又因为两段铁丝等长,所以这两段铁丝的总长为420cm.
答:这两段铁丝的总长为420cm. ……………………………………………8分
17.
16. (20011江苏镇江,12,2分)已知关于x的方程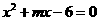 的一个根为2,则m=_____,另一根是_______.
的一个根为2,则m=_____,另一根是_______.
答案:1,-3
15. (2011上海,14,4分)某小区2011年屋顶绿化面积为2000平方米,计划2012年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是_________.
[答案]20%
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com